mcmc专题

MCMC平衡条件的一个反思

对于Marcov Chain平衡条件公式： Π=ΠP \Pi = \Pi P ，其中P为概率转移矩阵， Π \Pi为平衡概率状态。如果不注意，可以推导出下述公式： kΠ=kΠP k\Pi = k \Pi P，可能会得出 kΠ k\Pi也是P的平衡概率状态，这有一个错误，因为 ∑iΠ=1 \sum_i \Pi=1，而 ∑ikΠ=k≠1 \sum_i k\Pi=k \neq 1，

MLE、MAP、贝叶斯估计、MCMC、EM

机器学习中的MLE、MAP、贝叶斯估计 - 李文哲的文章 - 知乎 https://zhuanlan.zhihu.com/p/37215276 上面这篇文章对所提到的三种方法做了清晰的对比。总结图：另外文中总结：几点重要的Take-aways：每一个模型定义了一个假设空间，一般假设空间都包含无穷的可行解；MLE不考虑先验（prior)，MAP和贝叶斯估计则考虑先验（prior）；ML

马尔科夫蒙特卡洛方法（MCMC）+ Gibbs采样原理干货

最近要人工智能考试，复习被虐的不要不要的，老师一堂课讲的内容要自己再看几个小时…… MCMC和 Gibbs采样看书看得一脸懵逼，还好同学分享了一篇文章，看完豁然开朗，比《人工智能：一种现代的方法》强多了下面是链接： http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/

R 贝叶斯输出分析和诊断MCMC：coda包

描述该文档介绍了R语言中的`coda`包，这是一个用于处理Markov Chain Monte Carlo (MCMC)模拟输出分析和诊断的工具。包提供了函数来总结、绘制MCMC结果，以及进行收敛性诊断测试。函数总览数据输入与转换： bugs2jags: 将BUGS格式的数据转换为JAGS格式。 bugs2jags(infile, outfile) read.coda: 读取C

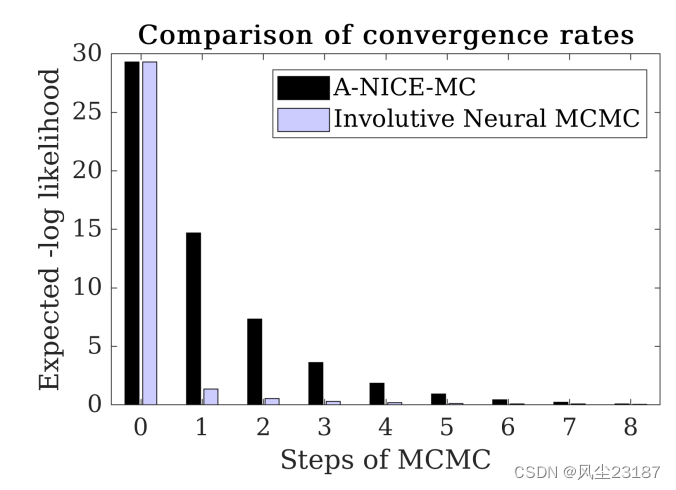
论文阅读：神经 MCMC 的深度内卷生成模型 Deep Involutive Generative Models for Neural MCMC

文章总结：本文提出了使用一种生成式的模型作为MCMC算法中的建议方式，并通过GAN进行优化。原文：Deep Involutive Generative Models for Neural MCMC 我们引入了深度内卷生成模型（一种深度生成建模的新架构），并使用它们来定义内卷神经 MCMC（一种快速神经 MCMC 的新方法）。内卷生成模型将概率核 G ( ϕ → ϕ ′ ) G( \

论文阅读：基于MCMC的能量模型最大似然学习剖析

On the Anatomy of MCMC-Based Maximum Likelihood Learning of Energy-Based Models 相关代码：点击本文只介绍关于MCMC训练的部分，由此可知，MCMC常常被用于训练EBM。最后一张图源于Implicit Generation and Modeling with Energy-Based Models 本研究调查

马尔科夫链MCMC采样算法和LDA Gibbs Sampling

本文转载统计之都上的一篇关于lda gibbs采样算法的介绍 http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/ 马氏链及其平稳分布马氏链的数学定义很简单 P(Xt+1=x|Xt,Xt−1,⋯)=P(Xt+1=x|Xt) 也就是状态转移的概率只依赖于前一个状态。我们先来看马氏链的一个具体的

深度学习理论知识入门【EM算法、VAE算法、GAN算法】和【RBM算法、MCMC算法、HMC算法】

目录深度学习理论知识入门首先，让我们了解第一个流程：现在，让我们看看第二个流程： EM算法GMM（高斯混合模型）深度学习理论知识入门首先，让我们了解第一个流程： EM（Expectation-Maximization）：EM算法是一种迭代优化算法，用于在存在潜在变量的统计模型中进行参数估计。它通过交替的E步骤（Expectation，期望）和M步骤（Maximiz

23-MCMC-马尔科夫链蒙特卡洛

文章目录 1.背景2.MCMC原理3.状态转移分布Q4. MCMC-采样方法4.1 蒙特卡罗方法(Monte Carlo Method)4.2 概率分布采样4.3 拒绝采样 Rejection Sampling4.4 重要性采样4.5 采样重要性重采样 5. MCMC-马尔科夫链5.1 马尔科夫性质5.2 细致分布证明平稳分布 6.MH算法(Metropolis-Hastings)7.吉布斯

大数据时代的采样定理：马尔可夫链蒙特卡洛(MCMC)与其python实现

大数据时代的特点是数据除了数量多、维度也将变多。那么传统的采样定理如果要构造合适的概率分布函数耗时且耗费大量算力。因此引入马尔科夫链的遍历性（Ergodicity）、常返性（recurrency）特点以及蒙特卡洛方法的大量实验逼近真实概率分布的原理实现多维的数据采样。从而构造概率分布函数。假设我们要采样的是一个二维正态分布 N（U,SIGMA），其中： U=（5，-1），方差sigma=（1

利用马尔可夫链蒙特卡洛（MCMC）进行贝叶斯线性回归和非线性回归的python代码（不调包）

1.利用MCMC进行线性回归本文的特点是不利用任何市面上的贝叶斯推断的包，将全过程自己实现，利用的是M-H采样算法，从而让读者对整个过程有深刻理解。本文呢不介绍任何数学原理。关于线性回归数学原理的解释请看：一般的线性回归，最小二乘和最大似然估计、最大后验估计视角: https://www.bilibili.com/video/BV1hW41167iL?spm_id_from=333