本文主要是介绍23-MCMC-马尔科夫链蒙特卡洛,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1.背景
- 2.MCMC原理
- 3.状态转移分布Q
- 4. MCMC-采样方法
- 4.1 蒙特卡罗方法(Monte Carlo Method)
- 4.2 概率分布采样
- 4.3 拒绝采样 Rejection Sampling
- 4.4 重要性采样
- 4.5 采样重要性重采样
- 5. MCMC-马尔科夫链
- 5.1 马尔科夫性质
- 5.2 细致分布证明平稳分布
- 6.MH算法(Metropolis-Hastings)
- 7.吉布斯采样算法Gibbs
- 8.MCMC-回顾
- 8.1采样的动机
- 8.2 好的样本定义
- 9. MCMC的采样思路以及面临的困难
- 9.1 MCMC问题
1.背景
MCMC作为一种随机采样的方法,全名“Markov Chain Monte Carlo”,MCMC有两部分组成,马尔科夫链(Markov Chain简称MC)和蒙特卡洛方法(Monte Carlo Simulation简称MC)组成。
如果我们模型中的P(X)非常的复杂,那么我们是无法直接在P(X)中进行采样的,我们知道的两种采样拒绝采样(Rejection-sampling)和重要性采样(Importance-sampling)是绕过了从P(X)中采样,而采用了提议分布q(X)(propose distribution),借助q(x)进行采样。这两种方法对于提议分布q(x)是有限制条件的,它们要求提议分布q(x)和样本分布P(x)接近,如果两个分布不接近,那么效果就非常的差。但通常情况下P(X)会非常的复杂,那么就会导致我们非常困难的去寻找一个分布q(X)让它跟P(X)接近且q(X)还要简单,这个目标太难了,我们根本没办法去做。为了解决上述找q(x)难的问题,所以我们就用到了MCMC方法进行采样。
MCMC方法是一大种类方法论,我们知道的MH算法和Gibbs算法是基于MCMC方法的两种具体实现。
2.MCMC原理
它借助于构建一套马氏链,用马氏链的性质(即:马氏链在经过若干步骤后,它从初始状态收敛到平稳分布)
我们假设马氏链的状态空间为: { 1 , 2 , . . , K } \{1,2,..,K\} {1,2,..,K},即:我们用下图表示可得:
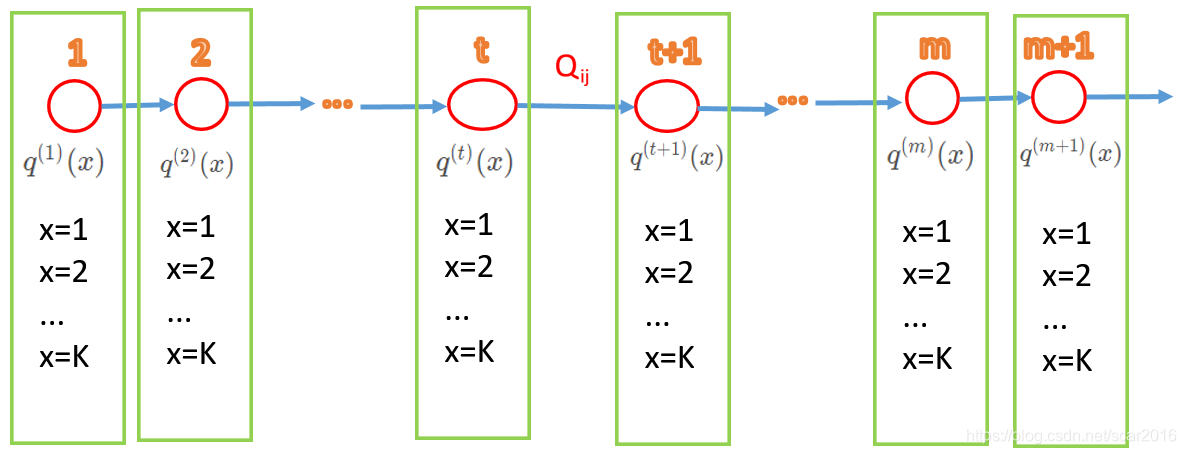
- 在第m时刻后, q ( m ) = q ( m + 1 ) = . . . = C 常 数 q^{(m)}=q^{(m+1)}=...=C_{常数} q(m)=q(m+1)=...=C常数,故满足此性质的分布叫做平稳分布。
- 我们的目标是希望最后平稳分布 q ( m ) q^{(m)} q(m)接近或甚至等于目标分布 P ( x ) P(x) P(x),这样我们就可以在平稳分布 q ( m ) q^{(m)} q(m)中采集样本 { x 1 , x 2 , . . . , x N } , \{x_1,x_2,...,x_N\}, {x1,x2,...,xN},那么我们就可以用采集的样本近似的代表目标分布 P ( X ) P(X) P(X).这样我们的采样的任务就完成了。
3.状态转移分布Q
为了更好的表达从 t 时刻到 t+1 时刻的状态变化,我们定义一个状态转移分布Q ,Q矩阵形式如下:
Q = ( Q 11 Q 12 . . . Q 1 k Q 21 Q 22 . . . Q 1 k ⋮ ⋮ ⋮ ⋮ Q k 1 Q k 2 . . . Q k k ) k × k (1) Q=\begin{pmatrix} Q_{11}&Q_{12}&...&Q_{1k}\\Q_{21}&Q_{22}&...&Q_{1k}\\\vdots&\vdots&\vdots&\vdots\\Q_{k1}&Q_{k2}&...&Q_{kk}\end{pmatrix}_{k \times k} \tag 1 Q=⎝⎜⎜⎜⎛Q11Q21⋮Qk1Q12Q22⋮Qk2......⋮...Q1kQ1k⋮Qkk⎠⎟⎟⎟⎞k×k(1)
- Q i j Q_{ij} Qij表示具体的概率值;一般默认Q分布为随机矩阵,其特征值绝对值小于等于1
- 满足 ∑ i = 1 k Q i 1 = ∑ i = 1 k Q i 2 = . . . = ∑ i = 1 k Q i k = 1 \sum_{i=1}^{k}Q_{i1}=\sum_{i=1}^{k}Q_{i2}=...=\sum_{i=1}^{k}Q_{ik}=1 ∑i=1kQi1=∑i=1kQi2=...=∑i=1kQik=1;列和为:1
- 满足 ∑ j = 1 k Q 1 j = ∑ j = 1 k Q 2 j = . . . = ∑ j = 1 k Q j k = 1 \sum_{j=1}^{k}Q_{1j}=\sum_{j=1}^{k}Q_{2j}=...=\sum_{j=1}^{k}Q_{jk}=1 ∑j=1kQ1j=∑j=1kQ2j=...=∑j=1kQjk=1;行和为:1
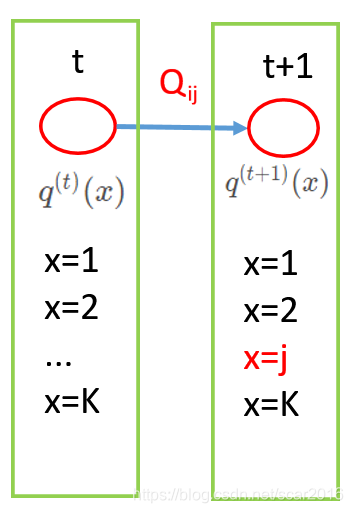
我们单独分析马氏链从 t 时刻到 t+1 时刻下的分布状态:如下图所示:
-
由下图可得:在 t+1 时刻时的 第 x=j 状态等于在 t 时刻状态下的K种状态的和再乘以转移矩阵;
q ( t + ! ) ( x = j ) = ∑ i = 1 K q ( t ) ( x = i ) ⋅ Q i j (2) q^{(t+!)}(x=j)=\sum_{i=1}^{K}q^{(t)}(x=i)·Q_{ij}\tag 2 q(t+!)(x=j)=i=1∑Kq(t)(x=i)⋅Qij(2)
我们定义 q ( t + 1 ) q^{(t+1)} q(t+1)为一个行向量:
q ( t + 1 ) = ( q ( t + 1 ) ( x = 1 ) , q ( t + 1 ) ( x = 2 ) , . . . , q ( t + 1 ) ( x = K ) ) 1 × k (3) q^{(t+1)}=(q^{(t+1)}(x=1),q^{(t+1)}(x=2),...,q^{(t+1)}(x=K))_{1 \times k}\tag {3} q(t+1)=(q(t+1)(x=1),q(t+1)(x=2),...,q(t+1)(x=K))1×k(3)
将公式2代入到公式3中可得:
q ( t + 1 ) = ( ∑ i = 1 K q ( t ) ( x = i ) ⋅ Q i 1 , ∑ i = 1 K q ( t ) ( x = i ) ⋅ Q i 2 , . . . , ∑ i = 1 K q ( t ) ( x = i ) ⋅ Q i k ) = q t ⋅ Q (4) q^{(t+1)}=(\sum_{i=1}^{K}q^{(t)}(x=i)·Q_{i1},\sum_{i=1}^{K}q^{(t)}(x=i)·Q_{i2},...,\sum_{i=1}^{K}q^{(t)}(x=i)·Q_{ik})=q^t·Q\tag {4} q(t+1)=(i=1∑Kq(t)(x=i)⋅Qi1,i=1∑Kq(t)(x=i)⋅Qi2,...,i=1∑Kq(t)(x=i)⋅Qik)=qt⋅Q(4)
故我们可以得到一个状态转移公式:
q ( t + 1 ) = q t ⋅ Q = . . . = q ( 1 ) ⋅ Q t (5) q^{(t+1)}=q^t·Q=...=q^{(1)}·Q^t\tag {5} q(t+1)=qt⋅Q=...=q(1)⋅Qt(5) -
随机矩阵Q有一个性质:特征值的绝对值小于等于1
我们对随机矩阵Q进行特征值分解:
Q = A Λ A − 1 (6) Q=A\Lambda A^{-1}\tag{6} Q=AΛA−1(6)
我们假设特征值只有一个为1,其余值得绝对值均小于1:
Λ = ( λ 11 ⋮ 1 . . . λ k k ) ; ∣ λ i i ∣ ≤ 1 (7) \Lambda=\begin{pmatrix} \lambda_{11}&&\\&\vdots&&\\&&1\\&&...& \lambda_{kk}\end{pmatrix}; |\lambda_{ii}|\le 1\tag{7} Λ=⎝⎜⎜⎜⎛λ11⋮1...λkk⎠⎟⎟⎟⎞;∣λii∣≤1(7)
则可得:
q ( t + 1 ) = q ( 1 ) ⋅ { A Λ A − 1 } t = q ( 1 ) ⋅ A Λ t A − 1 (8) q^{(t+1)}=q^{(1)}·\{{A\Lambda A^{-1}\}}^t=q^{(1)}·A\Lambda^{t}A^{-1}\tag {8} q(t+1)=q(1)⋅{AΛA−1}t=q(1)⋅AΛtA−1(8)
由 随 机 矩 阵 性 质 可 得 , 当 t → ∞ 时 , Λ t = ( 0 ⋮ 1 . . . 0 ) ; 由随机矩阵性质可得,当 t \rightarrow∞时,\Lambda^{t}=\begin{pmatrix} 0&&\\&\vdots&&\\&&1\\&&...& 0\end{pmatrix}; 由随机矩阵性质可得,当t→∞时,Λt=⎝⎜⎜⎜⎛0⋮1...0⎠⎟⎟⎟⎞;
所以我们代入求得:
第 m+1 时刻的分布 q ( m + 1 ) q^{(m+1)} q(m+1)
q ( m + 1 ) = q ( 1 ) ⋅ A Λ m A − 1 q^{(m+1)}=q^{(1)}·A\Lambda^{m}A^{-1} q(m+1)=q(1)⋅AΛmA−1
第 m+1 时刻的分布 q ( m + 1 ) q^{(m+1)} q(m+1)
q ( m + 2 ) = q ( 1 ) ⋅ A Λ m A − 1 ⋅ A Λ A − 1 = q ( 1 ) ⋅ A Λ m + 1 A − 1 (9) q^{(m+2)}=q^{(1)}·A\Lambda^{m}A^{-1}·A\Lambda A^{-1}=q^{(1)}·A\Lambda^{m+1}A^{-1}\tag {9} q(m+2)=q(1)⋅AΛmA−1⋅AΛA−1=q(1)⋅AΛm+1A−1(9) -
因为 Λ m = Λ m + 1 \Lambda^{m}=\Lambda^{m+1} Λm=Λm+1
可得:
q ( m + 2 ) = q ( m + 1 ) (10) q^{(m+2)}=q^{(m+1)}\tag {10} q(m+2)=q(m+1)(10)
结 论 : 当 t ≥ m 结论:当 t \geq m 结论:当t≥m时,可得:
q ( m + 1 ) = q ( m + 2 ) = . . . = q ( ∞ ) (10) q^{(m+1)}=q^{(m+2)}=...=q^{(∞)}\tag {10} q(m+1)=q(m+2)=...=q(∞)(10)
故以上可以证明在第 m 时刻后 ,其分布为同一个概率分布,即趋近于平稳,故为平稳分布。
4. MCMC-采样方法
之前我们讲到的变分推断(Variational Inference),我们知道推断inference的意思是我们看到数据X,我们假设有隐变量Z,我们在隐变量先验P(Z)已知的情况下,求解后验P(Z|X)的过程称之为推断Inference.推断分类如下:
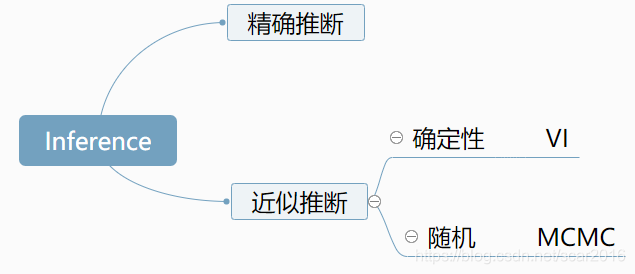
4.1 蒙特卡罗方法(Monte Carlo Method)
蒙特卡罗方法是一种基于采样的随机近似方法。主要用于做数值积分。我们的目标是为了求解后验概率P(Z|X),其中我们定义如下:
后 验 概 率 : P ( Z ∣ X ) (1) 后验概率:P(Z|X)\tag 1 后验概率:P(Z∣X)(1)
- Z:隐变量 latent data
- X:观测量 observed data
当我们知道分布P(z|x)时候,我们常见的做法是为了求在这个分布Z|X的背景下关于函数f(Z)的期望:
E Z ∣ X [ f ( Z ) ] = ∫ Z P ( Z ∣ X ) f ( Z ) d Z ≈ 1 N ∑ i = 1 N f ( z i ) (2) \mathbb{E}_{Z|X}[f(Z)]=\int_ZP(Z|X)f(Z)dZ≈\frac{1}{N}\sum_{i=1}^{N}f(z_i)\tag 2 EZ∣X[f(Z)]=∫ZP(Z∣X)f(Z)dZ≈N1i=1∑Nf(zi)(2) - 对于上式,我们问题在于怎样找到所需要的 z ( 1 ) , z ( 2 ) , . . . , z ( N ) ∼ P ( Z ∣ X ) z^{(1)},z^{(2)},...,z^{(N)}\sim P(Z|X) z(1),z(2),...,z(N)∼P(Z∣X),那么我们的就集中于如何在复杂分布P(Z|X)中进行采样。
三种基本采样方法:
- 概率分布采样
- 拒绝采样
- 重要性采样
4.2 概率分布采样
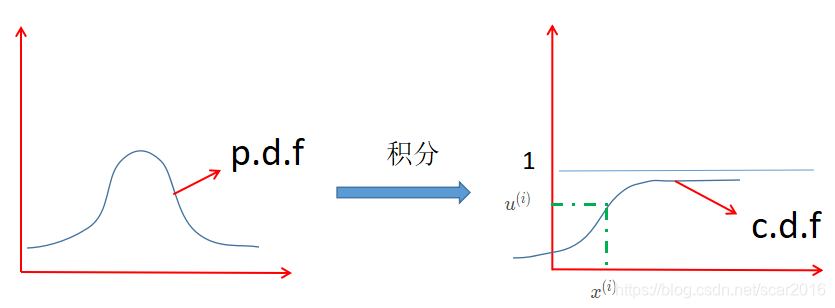
假设P(z)是我们要采样的概率分布,我们需要有一个均匀分布 U ∈ [ 0 , 1 ] U \in [0,1] U∈[0,1],用计算机的随机数来采集N个数据集 { u ( 1 ) , u ( 2 ) , . . . , u ( N ) } ∈ U = [ 0 , 1 ] , x ( i ) \{u^{(1)},u^{(2)},...,u^{(N)}\}\in U=[0,1],x^{(i)} {u(1),u(2),...,u(N)}∈U=[0,1],x(i),我们定义p.d.f为概率密度函数,c.d.f为概率分布函数;
-
概率分布采样步骤如下:

我们对于这种概率采样方法看起来非常的有用,但是我们发现,当我们的概率密度函数十分的复杂的时候,我们就没办法直接求得c.d.f,在用 u ( i ) u^{(i)} u(i)通过c.d.f反向求 x ( i ) x^{(i)} x(i)时出现问题,即:
x ( i ) = c . d . f ( − 1 ) ( u ( i ) ) (3) x^{(i)}=c.d.f^{(-1)}(u^{(i)})\tag 3 x(i)=c.d.f(−1)(u(i))(3) -
当我们c.d.f很复杂的时候,我们就没办法直接求得 x ( i ) x^{(i)} x(i)
4.3 拒绝采样 Rejection Sampling
由于对于目标分布p(z)十分的难估计和采样,所以我们假设一个简单的分布q(z),进行辅助采样,具体如下:
-
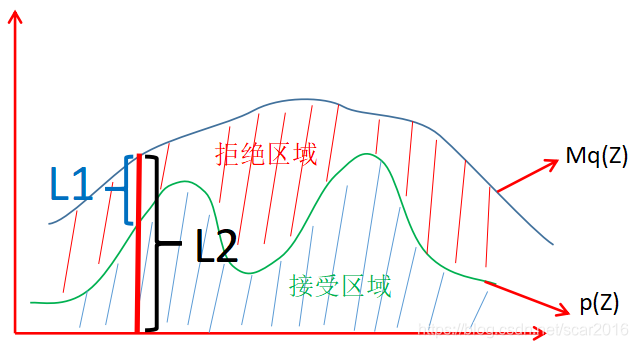
我们定义一个叫proposal distribution的分布为q(Z) ,对于任意 ∀ z i \forall z_i ∀zi,保证如下:
M ⋅ q ( z ( i ) ) ≥ p ( z ( i ) ) (4) M·q(z^{(i)})\geq p(z^{(i)})\tag 4 M⋅q(z(i))≥p(z(i))(4)
-
我们定义接受率为α=L1/L2: 0≤α≤1;
α = p ( z ( i ) ) M ⋅ q ( z ( i ) ) (5) \alpha=\frac{p(z^{(i)})}{M·q(z^{(i)})}\tag 5 α=M⋅q(z(i))p(z(i))(5)
采样步骤如下:
- 从q(z)分布中采样得到 z ( i ) 即 : z ( i ) ∼ q ( z ) z^{(i)}即:z^{(i)}\sim q(z) z(i)即:z(i)∼q(z)
- 从均匀分布U[0,1]从采样得到 u ( i ) u^{(i)} u(i)
- 如果 u ( i ) ≤ α u^{(i)} \leq \alpha u(i)≤α,那么我们就接受 z ( i ) z^{(i)} z(i),否则拒绝 z ( i ) z^{(i)} z(i).
综上所述,我们非常的依赖q(z)的形式,红色部分为我们拒绝区域,绿色部分为我们的拒绝区域。但这个分布又有很多的缺点,当M·q(z)远大于p(z)时,那么拒绝区域就非常的大,导致采样经常失败。就会导致采样率非常的低。所以这个采样方法非常的依赖于M·q(z)的选择,但实际上,我们发现p(z)十分的复杂,我们根本就没有办法来得到那么准确的结果,特别是采样 cost 非常高的话,经常性的采样失败带来的损失是很大的。
4.4 重要性采样
重要性采样并不是对概率进行采样,而是对概率分布的期望进行采样,即:
E p ( z ) [ f ( z ) ] = ∫ z p ( z ) ⋅ f ( z ) d z = ∫ z p ( z ) q ( z ) ⋅ q ( z ) f ( z ) d z (6) \mathbb{E}_{p(z)}[f(z)]=\int_zp(z)·f(z)dz=\int_z\frac{p(z)}{q(z)}·q(z)f(z)dz\tag 6 Ep(z)[f(z)]=∫zp(z)⋅f(z)dz=∫zq(z)p(z)⋅q(z)f(z)dz(6)
= ∫ z f ( z ) p ( z ) q ( z ) ⋅ q ( z ) d z = E q ( z ) [ f ( z ) p ( z ) q ( z ) ] ≈ 1 N ∑ i = 1 N [ f ( z ( i ) ) p ( z ( i ) ) q ( z ( i ) ) ] (7) =\int_zf(z)\frac{p(z)}{q(z)}·q(z)dz=\mathbb{E}_{q(z)}[f(z)\frac{p(z)}{q(z)}]≈\frac{1}{N}\sum_{i=1}^{N}[f(z^{(i)})\frac{p(z^{(i)})}{q(z^{(i)})}]\tag 7 =∫zf(z)q(z)p(z)⋅q(z)dz=Eq(z)[f(z)q(z)p(z)]≈N1i=1∑N[f(z(i))q(z(i))p(z(i))](7)
- 我们假设样本 z ( i ) z^{(i)} z(i)是在分布q(z)中进行采样的。即: z ( i ) ∼ q ( z ) , i = 1 , 2 , . . . , N z^{(i)}\sim q(z),i=1,2,...,N z(i)∼q(z),i=1,2,...,N
- 我们定义权重 w e i g h t = p ( z ( i ) ) q ( z ( i ) ) weight=\frac{p(z^{(i)})}{q(z^{(i)})} weight=q(z(i))p(z(i))
- 重要性采样也是严重的依赖于p(z)与q(z)的相似性程度。用来平衡不同的概率密度值之间的差距。同样重要性采样也可能
会出现一些问题,就是两个分布之间的差距太大了话,总是采样采不到重要的样本,采的可能都是实际分布概率值小的部分。也就是采样效率不均匀的问题。在这个基础上,我们进一步提出了 SamplingImportance Resampling。
4.5 采样重要性重采样
经过重要性采样后,我们得到了 N 个样本点,以及对应的权重。那么我用权重来作为采样的概率,重新测采样出 N 个样本。也就是如下图所示
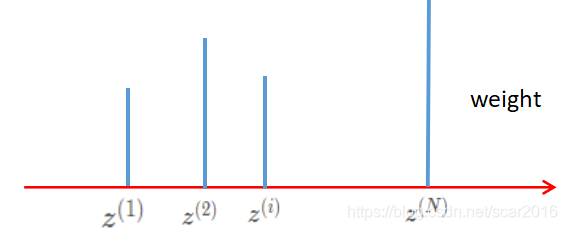
通过二次采样可以降低采样不平衡的问题。至于为什么呢?大家想一想,我在这里表达一下自己的看法。p(zi)/q(zi) 是 Weight,如果 Weight 比较大的话,说明 p(zi) 比较大而 q(zi) 比较的小,也就是我们通过 q(zi) 采出来的数量比较少。那么我们按权重再来采一次,就可以增加采到重要性样本的概率,成功的弥补了重要性采样带来的缺陷,有效的弥补采样不均衡的问题。
5. MCMC-马尔科夫链
我们知道蒙特卡罗方法[Monte Carlo Method]是一个基于随机采样的近似方法,我们定义马尔科夫链[Markov Chain]是时间和状态都是离散的链。随机过程就是研究对象是一个随机对象序列 { X 1 , X 2 , . . . , X N } , 而 不 是 一 个 单 独 的 随 机 变 量 X . \{X_1,X_2,...,X_N\},而不是一个单独的随机变量X. {X1,X2,...,XN},而不是一个单独的随机变量X.
5.1 马尔科夫性质
马氏链定义是它的随机变量序列满足马尔科夫性质;马尔科夫性质定义:当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态;换句话说,在给定现在状态时,它与过去状态(即该过程的历史路径)是条件独立的,那么此随机过程即具有马尔可夫性质。具有马尔可夫性质的过程通常称之为马尔可夫过程;简单来说:在给定当前状态下,未来只依赖于当前,未来跟过去无关,就是英雄不问出处,未来只取决于现在,跟过去没任何关系。
-
齐次(一阶)马尔科夫链的数学表达:
P ( X t + 1 = x ∣ X 1 , X 2 , . . . , X t ) = P ( X t + 1 = x ∣ X t ) (8) P(X_{t+1}=x|X_1,X_2,...,X_t)=P(X_{t+1}=x|X_t)\tag 8 P(Xt+1=x∣X1,X2,...,Xt)=P(Xt+1=x∣Xt)(8) -
转移矩阵 P , 每 一 个 转 移 矩 阵 为 [ P i j ] P,每一个转移矩阵为[P_{ij}] P,每一个转移矩阵为[Pij]
P i j = P ( X t + 1 = j ∣ X t = i ) (9) P_{ij}=P(X_{t+1}=j|X_{t}=i)\tag 9 Pij=P(Xt+1=j∣Xt=i)(9) -
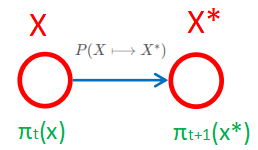
马尔科夫链图形化表达:

我们来局部分析概率从 X 到 X ∗ X到X^* X到X∗
-
假如存在一个向量 π = [ π ( 1 ) , π ( 2 ) , . . . , π ( N ) , . . . ] , 假 如 有 一 个 概 率 分 布 π 满 足 : ∑ i = 1 ∞ π ( i ) = 1 \pi=[\pi^{(1)},\pi^{(2)},...,\pi^{(N)},...],假如有一个概率分布\pi满足:\sum_{i=1}^{\infty}\pi^{(i)}=1 π=[π(1),π(2),...,π(N),...],假如有一个概率分布π满足:∑i=1∞π(i)=1,且满足如下公式:那么我们就称这个序列 { π ( k ) } \{\pi(k)\} {π(k)}为马氏链 X t X_t Xt的平稳分布。
π t + 1 ( X ∗ ) = ∫ π t ( X ) ⋅ P ( X ⟼ X ∗ ) d x (10) \pi _{t+1}(X^*)=\int \pi _{t}(X)·P(X\longmapsto X^*)dx\tag {10} πt+1(X∗)=∫πt(X)⋅P(X⟼X∗)dx(10) -
重点:我们引入平稳分布的目的是当我们要通过采样的方式来求出后验分布P(Z)时,如果我们把P(Z)看作平稳分布的 { π ( k ) } \{\pi(k)\} {π(k)},我们就可以构造一系列的 { X 1 , X 2 , . . . . , X N } \{X_1,X_2,....,X_N\} {X1,X2,....,XN}的马氏链,让这个马氏链的 { π ( k ) } \{\pi(k)\} {π(k)}来逼近于P(Z)。
-
细致平稳概念(detailed balance)
π ( X ) ⋅ P ( X ⟼ X ∗ ) = π ( X ∗ ) ⋅ P ( X ∗ ⟼ X ) (11) \pi(X)·P(X\longmapsto X^*)=\pi(X^*)·P(X^*\longmapsto X)\tag {11} π(X)⋅P(X⟼X∗)=π(X∗)⋅P(X∗⟼X)(11) -
detailed-balance是平稳分布的充分非必要条件。
-
P ( X ⟼ X ∗ ) : 表 示 条 件 概 率 , 相 当 于 P ( X ∣ X ∗ ) P(X\longmapsto X^*):表示条件概率,相当于P(X| X^*) P(X⟼X∗):表示条件概率,相当于P(X∣X∗)

5.2 细致分布证明平稳分布
∫ π ( X ) ⋅ P ( X ⟼ X ∗ ) d x \int\pi(X)·P(X\longmapsto X^*)dx ∫π(X)⋅P(X⟼X∗)dx
我们知道细致分布为: π ( X ) ⋅ P ( X ⟼ X ∗ ) = π ( X ∗ ) ⋅ P ( X ∗ ⟼ X ) \pi(X)·P(X\longmapsto X^*)=\pi(X^*)·P(X^*\longmapsto X) π(X)⋅P(X⟼X∗)=π(X∗)⋅P(X∗⟼X)
= ∫ π ( X ∗ ) ⋅ P ( X ∗ ⟼ X ) d x =\int\pi(X^*)·P(X^*\longmapsto X)dx =∫π(X∗)⋅P(X∗⟼X)dx
= π ( X ∗ ) ⋅ ∫ P ( X ∗ ⟼ X ) d x ⏟ = 1 =\pi(X^*)·\underbrace{\int P(X^*\longmapsto X)dx}_{=1} =π(X∗)⋅=1 ∫P(X∗⟼X)dx
= π ( X ∗ ) =\pi(X^*) =π(X∗)
结 论 : π ( X ∗ ) = ∫ π ( X ) ⋅ P ( X ⟼ X ∗ ) d x ; [ 平 稳 分 布 公 式 ] 结论:\pi(X^*)=\int\pi(X)·P(X\longmapsto X^*)dx;[平稳分布公式] 结论:π(X∗)=∫π(X)⋅P(X⟼X∗)dx;[平稳分布公式]
- 注:为了找到平稳分布,我们不方便用平稳分布公式来找,我们曲线救国的方式用细致分布公式来找到平稳分布。
6.MH算法(Metropolis-Hastings)
我们关心的是我们的后验概率P(Z),为了求关于后验概率相关函数的期望即:
E P ( Z ) [ f ( z ) ] = ∫ z f ( z ) ⋅ p ( z ) d z ≈ 1 N ∑ i = 1 N f ( z ( i ) ) (12) \mathbb{E}_{P(Z)}[f(z)]=\int_zf(z)·p(z)dz≈\frac{1}{N}\sum_{i=1}^{N}f(z^{(i)})\tag{12} EP(Z)[f(z)]=∫zf(z)⋅p(z)dz≈N1i=1∑Nf(z(i))(12)
- 我们在概率分布P(Z)中不断的采样,得到N个 z ( i ) ∼ p ( z ) z^{(i)}\sim p(z) z(i)∼p(z).但实际上我们从P(Z)中采样是十分的困难,所以我们就用MCMC法进行采样。
我们由细致分布公式可知: π ( X ) ⋅ P ( X ⟼ X ∗ ) = π ( X ∗ ) ⋅ P ( X ∗ ⟼ X ) \pi(X)·P(X\longmapsto X^*)=\pi(X^*)·P(X^*\longmapsto X) π(X)⋅P(X⟼X∗)=π(X∗)⋅P(X∗⟼X),我们所求最终的平稳分布为 π ( X ) \pi(X) π(X),所以我们把目标后验分布P(Z)看作平稳分布的 π ( X ) \pi(X) π(X),通过构造一个马氏链,让这个马氏链最终趋向于平稳分布P(Z);那么我们的问题转换为怎么找到detailed balance里的转移矩阵,使得这个马氏链趋向于平稳P(Z).
-
构造转移矩阵Q使得满足detailed-balance:
P ( Z ) ⋅ Q ( Z ⟼ Z ∗ ) ⋅ α ( z , z ∗ ) ⏟ P ( Z ⟼ Z ∗ ) = P ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) ⋅ α ( z ∗ , z ) ⏟ P ( Z ∗ ⟼ Z ) (13) P(Z)·\underbrace{Q(Z\longmapsto Z^*)·\alpha(z,z^*)}_{P(Z\longmapsto Z^*)}=P(Z^*)·\underbrace{Q(Z^*\longmapsto Z)·\alpha(z^*,z)}_{P(Z^*\longmapsto Z)}\tag{13} P(Z)⋅P(Z⟼Z∗) Q(Z⟼Z∗)⋅α(z,z∗)=P(Z∗)⋅P(Z∗⟼Z) Q(Z∗⟼Z)⋅α(z∗,z)(13) -
α ( z , z ∗ ) : \alpha(z,z^*): α(z,z∗):表示接受率。
α ( z , z ∗ ) = m i n ( 1 , p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) p ( Z ) ⋅ Q ( Z ⟼ Z ∗ ) ) (14) \alpha(z,z^*)=min( 1,\frac{p(Z^*)·Q(Z^*\longmapsto Z)}{p(Z)·Q(Z\longmapsto Z^*)})\tag{14} α(z,z∗)=min(1,p(Z)⋅Q(Z⟼Z∗)p(Z∗)⋅Q(Z∗⟼Z))(14) -
Q ( Z ∗ ⟼ Z ) = Q ( Z ∣ Z ∗ ) ; Q ( Z ⟼ Z ∗ ) = Q ( Z ∗ ∣ Z ) Q(Z^*\longmapsto Z)=Q(Z|Z^*);Q(Z\longmapsto Z^*)=Q(Z^*|Z) Q(Z∗⟼Z)=Q(Z∣Z∗);Q(Z⟼Z∗)=Q(Z∗∣Z)
P ( Z ) ⋅ P ( Z ⟼ Z ∗ ) = P ( Z ∗ ) ⋅ P ( Z ∗ ⟼ Z ) (15) P(Z)·{P(Z\longmapsto Z^*)}=P(Z^*)·{P(Z^*\longmapsto Z)}\tag{15} P(Z)⋅P(Z⟼Z∗)=P(Z∗)⋅P(Z∗⟼Z)(15)
证:
P ( Z ) Q ( Z ⟼ Z ∗ ) ⋅ α ( z , z ∗ ) = P ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) ⋅ α ( z ∗ , z ) (16) P(Z)Q(Z\longmapsto Z^*)·\alpha(z,z^*)=P(Z^*)·Q(Z^*\longmapsto Z)·\alpha(z^*,z)\tag{16} P(Z)Q(Z⟼Z∗)⋅α(z,z∗)=P(Z∗)⋅Q(Z∗⟼Z)⋅α(z∗,z)(16)
证明如下:
P ( Z ) Q ( Z ⟼ Z ∗ ) ⋅ α ( z , z ∗ ) P(Z)Q(Z\longmapsto Z^*)·\alpha(z,z^*) P(Z)Q(Z⟼Z∗)⋅α(z,z∗)
= P ( Z ) Q ( Z ⟼ Z ∗ ) ⋅ m i n ( 1 , p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) p ( Z ) ⋅ Q ( Z ⟼ Z ∗ ) ) =P(Z)Q(Z\longmapsto Z^*)·min( 1,\frac{p(Z^*)·Q(Z^*\longmapsto Z)}{p(Z)·Q(Z\longmapsto Z^*)}) =P(Z)Q(Z⟼Z∗)⋅min(1,p(Z)⋅Q(Z⟼Z∗)p(Z∗)⋅Q(Z∗⟼Z))
= ⋅ m i n ( P ( Z ) Q ( Z ⟼ Z ∗ ) , p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) ) =·min( P(Z)Q(Z\longmapsto Z^*),p(Z^*)·Q(Z^*\longmapsto Z)) =⋅min(P(Z)Q(Z⟼Z∗),p(Z∗)⋅Q(Z∗⟼Z))
= p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) ) ⋅ m i n ( p ( Z ) ⋅ Q ( Z ⟼ Z ∗ ) p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) , 1 ) =p(Z^*)·Q(Z^*\longmapsto Z))·min( \frac{p(Z)·Q(Z\longmapsto Z^*)}{p(Z^*)·Q(Z^*\longmapsto Z)},1) =p(Z∗)⋅Q(Z∗⟼Z))⋅min(p(Z∗)⋅Q(Z∗⟼Z)p(Z)⋅Q(Z⟼Z∗),1)
由于可得:
α ( z ∗ , z ) = m i n ( p ( Z ) ⋅ Q ( Z ⟼ Z ∗ ) p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) , 1 ) (17) \alpha(z^*,z)=min( \frac{p(Z)·Q(Z\longmapsto Z^*)}{p(Z^*)·Q(Z^*\longmapsto Z)},1)\tag{17} α(z∗,z)=min(p(Z∗)⋅Q(Z∗⟼Z)p(Z)⋅Q(Z⟼Z∗),1)(17)
所以原式可得:
P ( Z ) Q ( Z ⟼ Z ∗ ) ⋅ α ( z , z ∗ ) = p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) ) ⋅ α ( z ∗ , z ) (18) P(Z)Q(Z\longmapsto Z^*)·\alpha(z,z^*)=p(Z^*)·Q(Z^*\longmapsto Z))·\alpha(z^*,z)\tag{18} P(Z)Q(Z⟼Z∗)⋅α(z,z∗)=p(Z∗)⋅Q(Z∗⟼Z))⋅α(z∗,z)(18)
证毕,公式16成立!
结论:只要我们取接受率 α ( z ∗ , z ) \alpha(z^*,z) α(z∗,z),,那么马氏链就满足detailed-balance 的条件,从而得到平稳分布。
α ( z , z ∗ ) = m i n ( 1 , p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) p ( Z ) ⋅ Q ( Z ⟼ Z ∗ ) ) (19) \alpha(z,z^*)=min( 1,\frac{p(Z^*)·Q(Z^*\longmapsto Z)}{p(Z)·Q(Z\longmapsto Z^*)})\tag{19} α(z,z∗)=min(1,p(Z)⋅Q(Z⟼Z∗)p(Z∗)⋅Q(Z∗⟼Z))(19)
- P(Z) 在转移矩阵 Q(Z|Z∗)α(Z∗, Z) 下是一个平稳分布,也就是一个马尔可夫链,通过在这个马尔可夫链中采样就可以得到我们的相应的数据样本点了。实际上这就是大名鼎鼎的 MetropolisHastings 采样法。
Metropolis-Hastings Sampling (M.H算法具体采样步骤):
- 1 > 我们用计算机随机数从均匀分布U(0,1)中随机采样得到 u ( i ) , 即 可 得 : u ( i ) ∼ U ( 0 , 1 ) u^{(i)},即可得:u^{(i)}\sim U(0,1) u(i),即可得:u(i)∼U(0,1)
- 2 > 我们在分布 Q ( Z ∣ Z ( i − 1 ) ) Q(Z|Z^{(i-1)}) Q(Z∣Z(i−1))中采样得到样本 Z ∗ Z^* Z∗
- 3 > 我们定义 α ( z , z ∗ ) = m i n ( 1 , p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) p ( Z ) ⋅ Q ( Z ⟼ Z ∗ ) ) \alpha(z,z^*)=min( 1,\frac{p(Z^*)·Q(Z^*\longmapsto Z)}{p(Z)·Q(Z\longmapsto Z^*)}) α(z,z∗)=min(1,p(Z)⋅Q(Z⟼Z∗)p(Z∗)⋅Q(Z∗⟼Z))
- 4 > 如果 u ( i ) ≤ α 时 , 可 得 Z ( i ) = Z ∗ , 否 则 Z ( i ) = Z ( i − 1 ) u^{(i)}\leq \alpha时,可得Z^{(i)}=Z^*,否则 Z^{(i)}=Z^{(i-1)} u(i)≤α时,可得Z(i)=Z∗,否则Z(i)=Z(i−1),这样执行了 N 次,就可以得到 {Z(1), Z(2)
, · · · , Z(N)} 个样本点
注意:对于后验概率P(Z)来说,我们隐含了一个重要的条件,即:
P ( Z ) = p ^ ( Z ) Z p (20) P(Z)=\frac{\hat{p}(Z)}{Z_p}\tag{20} P(Z)=Zpp^(Z)(20)
- Z p : Z_p: Zp:表示归一化因子,是求不出来的,但在接受率上正好分子与分布约掉了,所以没影响接受率。Pˆ(Z) = likelihood × prior。所以这里的 P(Z) 和 P(Z∗) 就是 Pˆ(Z) 和 Pˆ(Z∗)。由于归一化因子被抵消了,干脆就直接写成了 P ( Z ) 和 P ( Z ∗ ) P(Z) 和 P(Z^∗) P(Z)和P(Z∗)。
7.吉布斯采样算法Gibbs
吉布斯算法采样本质上也是属于MH采样,不过是一种特殊的MH采样。Gibbs采样假设要采样的分布P(Z)维度非常的高。即:
P ( Z ) = P ( Z 1 , Z 2 , . . . , Z N ) (21) P(Z)=P(Z_1,Z_2,...,Z_N)\tag{21} P(Z)=P(Z1,Z2,...,ZN)(21)
- 采样第 i 维时,我们固定其他N-1个维度;即:
Z i ∼ P ( Z i ∣ Z 1 , 2 , . . . , i − 1 , i + 1 , . . . N ) (22) Z_i \sim P(Z_i|Z_{1,2,...,i-1,i+1,...N})\tag{22} Zi∼P(Zi∣Z1,2,...,i−1,i+1,...N)(22)
举例说明:假如 P ( Z ) = P ( Z 1 , Z 2 , Z 3 ) P(Z)=P(Z_1,Z_2,Z_3) P(Z)=P(Z1,Z2,Z3),三维数据分布 - 首先我们给定初始值 Z 1 ( 0 ) , Z 2 ( 0 ) , Z 3 ( 0 ) Z_1^{(0)},Z_2^{(0)},Z_3^{(0)} Z1(0),Z2(0),Z3(0)
- 在 t + 1 时刻采样
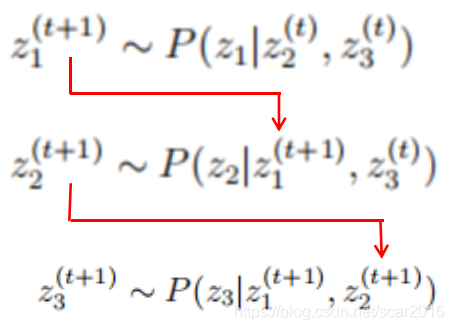
我们知道MH算法中的接受率α表示如下,我们现在可以用Gibbs算法来类比MH算法的接受率:
- MH 算法接受率α:
α ( z , z ∗ ) = m i n ( 1 , p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) p ( Z ) ⋅ Q ( Z ⟼ Z ∗ ) ) (23) \alpha(z,z^*)=min( 1,\frac{p(Z^*)·Q(Z^*\longmapsto Z)}{p(Z)·Q(Z\longmapsto Z^*)})\tag{23} α(z,z∗)=min(1,p(Z)⋅Q(Z⟼Z∗)p(Z∗)⋅Q(Z∗⟼Z))(23)
p ( Z ∗ ) ⋅ Q ( Z ∗ ⟼ Z ) p ( Z ) ⋅ Q ( Z ⟼ Z ∗ ) ) \frac{p(Z^*)·Q(Z^*\longmapsto Z)}{p(Z)·Q(Z\longmapsto Z^*)}) p(Z)⋅Q(Z⟼Z∗)p(Z∗)⋅Q(Z∗⟼Z))
- p ( Z ∗ ) = p ( Z ∗ ∣ Z − i ∗ ) P ( Z − i ∗ ) p(Z^*)=p(Z^*|Z_{-i}^*)P(Z_{-i}^*) p(Z∗)=p(Z∗∣Z−i∗)P(Z−i∗)概率拆分
- Q ( Z ∗ ⟼ Z ) = P ( Z ∣ Z ∗ ) Q(Z^*\longmapsto Z)=P(Z|Z^*) Q(Z∗⟼Z)=P(Z∣Z∗)条件概率
- P ( Z ) = P ( Z i ∣ Z − i ) ⋅ P ( Z − i ) P(Z)=P(Z_i|Z_{-i})·P(Z_{-i}) P(Z)=P(Zi∣Z−i)⋅P(Z−i)概率拆分
- Q ( Z ⟼ Z ∗ ) = P ( Z ∗ ∣ Z ) Q(Z\longmapsto Z^*)=P(Z^*|Z) Q(Z⟼Z∗)=P(Z∗∣Z)条件概率
= p ( Z ∗ ∣ Z − i ∗ ) P ( Z − i ∗ ) ⋅ P ( Z ∣ Z ∗ ) P ( Z i ∣ Z − i ) ⋅ P ( Z − i ) ⋅ P ( Z ∗ ∣ Z ) (24) =\frac{p(Z^*|Z_{-i}^*)P(Z_{-i}^*)·P(Z|Z^*)}{P(Z_i|Z_{-i})·P(Z_{-i})·P(Z^*|Z)}\tag{24} =P(Zi∣Z−i)⋅P(Z−i)⋅P(Z∗∣Z)p(Z∗∣Z−i∗)P(Z−i∗)⋅P(Z∣Z∗)(24) - P ( Z ∣ Z ∗ ) = P ( Z i ∣ Z − i ∗ ) P(Z|Z^*)=P(Z_i|Z_{-i}^*) P(Z∣Z∗)=P(Zi∣Z−i∗),对于Gibbs算法来说成立
- P ( Z ∗ ∣ Z ) = P ( Z i ∗ ∣ Z − i ) P(Z^*|Z)=P(Z_i^*|Z_{-i}) P(Z∗∣Z)=P(Zi∗∣Z−i),对于Gibbs算法来说成立
- P ( Z − i ∗ ) = P ( Z − i ) : 因 为 每 次 采 样 都 是 固 定 其 他 分 量 , 所 以 概 率 相 等 , 且 两 项 等 价 : Z − i ∗ = Z − i P(Z_{-i}^*)=P(Z_{-i}):因为每次采样都是固定其他分量,所以概率相等,且两项等价:Z_{-i}^*=Z_{-i} P(Z−i∗)=P(Z−i):因为每次采样都是固定其他分量,所以概率相等,且两项等价:Z−i∗=Z−i
= p ( Z ∗ ∣ Z − i ∗ ) P ( Z − i ∗ ) ⋅ P ( Z i ∣ Z − i ∗ ) P ( Z i ∣ Z − i ∗ ) ⋅ P ( Z − i ) ⋅ P ( Z i ∗ ∣ Z − i ∗ ) = 1 (25) =\frac{p(Z^*|Z_{-i}^*)P(Z_{-i}^*)·P(Z_i|Z_{-i}^*)}{P(Z_i|Z_{-i}^*)·P(Z_{-i})·P(Z_i^*|Z_{-i}^*)}=1\tag{25} =P(Zi∣Z−i∗)⋅P(Z−i)⋅P(Zi∗∣Z−i∗)p(Z∗∣Z−i∗)P(Z−i∗)⋅P(Zi∣Z−i∗)=1(25)
所以,对于吉布斯采样算法,其接受率为1,所以吉布斯采样就是特殊的MH算法,且接受率为1,每次从状态转移矩阵 Q ( Z ∣ Z ( t ) ) = P ( Z t ∗ ∣ Z − i ) Q(Z|Z^{(t)})=P(Z_t^*|Z_{-i}) Q(Z∣Z(t))=P(Zt∗∣Z−i)中采样得到 Z i ∗ Z_i^* Zi∗即可。这里我们需要额外提醒一下,使用 Gibbs Sampling 是有使用前提的,也就是固定其他维度后的一
维分布时方便进行采样的,如果固定其他维度的时候得到的一维分布仍然是非常难进行采样的,那么
使用 Gibbs Sampling 也是没有用的。
8.MCMC-回顾
8.1采样的动机
蒙特卡洛方法主要是为了做采样的。那我们采样的动机是什么?在机器学习中我们为什么要去采样。
- 采样的本身就是常见的任务
在我们的机器学习中,我们经常出现我们已经学出了一个模型P(X),这个模型是一堆数据,有一种任务是让你从概率分布模型中产生一些样本,这个就是采样的过程。例如,P(X)是一个生成模型,表示一堆图片,让你生成一堆新的图片,那这个其实就是当你把模型学好后就可以从这个分布中采样新的数据样本即可。 - 求和或求积分的简化
∫ x P ( X ) f ( x ) d x = E p ( x ) [ f ( x ) ] (26) \int_x P(X)f(x)dx=\mathbb{E}_{p(x)}[f(x)]\tag{26} ∫xP(X)f(x)dx=Ep(x)[f(x)](26)
从概率分布P(X)中采样出N个样本 { X ( 1 ) , X ( 2 ) , . . . X ( N ) , } ∈ P ( X ) \{X^{(1)},X^{(2)},...X^{(N)},\}\in P(X) {X(1),X(2),...X(N),}∈P(X),那么我们可以用如下公式代替期望:
E p ( x ) [ f ( x ) ] ≈ 1 N ∑ i = 1 N f ( X ( i ) ) (27) \mathbb{E}_{p(x)}[f(x)]≈\frac{1}{N}\sum_{i=1}^{N}f(X^{(i)})\tag{27} Ep(x)[f(x)]≈N1i=1∑Nf(X(i))(27)
8.2 好的样本定义
- 样本趋向于高概率区域
我们希望在分布P(X)中采样的分布都是在高概率区域,这样采样才有意义,比如,我们希望选取的人大代表应该始终代表最广大人民的根本利益,所以选择的应该是在大部人群中选取,而不是在总在那些富豪之间选取,毕竟富豪在整个人口分布中占据小部分。 - 样本与样本之间最好是相互独立的。
我们最好是在不同种类中选取相互独立的样本,这样才能更好的表达整体数据,而不是总选择相关的样本。
但在实际过程中,我们采样是十分困难的,比如无向图模型中的P(X)中,往往有一个归一化因子Z,满足如下:
P ( X ) = 1 ⋅ P ^ ( X ) Z (28) P(X)=\frac{1·\hat{P}(X)}{Z}\tag{28} P(X)=Z1⋅P^(X)(28)
- Z:划分函数:partition-function;归一化常数Z,当维度很大的时候,往往难计算出来 Z = ∫ x P ^ ( X ) d x Z=\int_x \hat{P}(X)dx Z=∫xP^(X)dx,那么我们就很难直接在P(X)中进行采样【详见概率分布采样】。
所以我们遇到的困难如下:
- 划分函数Z是十分难求出来的。
- 即使划分函数Z求出来了,也会因为高维数据遇到高维的维度诅咒问题。
比如: X ∈ { 1 , 2 , . . . , K } p , 那 么 总 的 状 态 空 间 : K P X\in\{1,2,...,K\}^p,那么总的状态空间:K^P X∈{1,2,...,K}p,那么总的状态空间:KP,这个维度就呈现指数级增长,那么我们就没办法遍历所有数据。
正因为我们发现直接采样P(X)十分的困难,所以我们才另辟蹊径采取了拒绝采样和重要性采样。借助简单的辅助分布q(X)来代替复杂的P(X)来进行采样,来绕过直接采样P(X);
MCMC的思想是试图构建一个马氏链去逼近最终的目标分布,比如MH算法采样和Gibbs算法采样。
9. MCMC的采样思路以及面临的困难
蒙特卡洛方法的马尔科夫链经过若干周期后会趋向于平稳分布,我们假设状态空间为离散 { 1 , 2 , . . . , K } \{1,2,...,K\} {1,2,...,K},定义状态转移矩阵为 Q = [ Q i j ] k × k Q=[Q_{ij}]_{k\times k} Q=[Qij]k×k,即假定到达m步后马氏链趋向于平稳分布。因此启发我们和采样方法结合起来产生MCMC。MCMC其实是一套方法论,我们常用的是MH算法采样和吉布斯算法采样。
- MCMC思路:
利用马尔科夫链收敛于平稳分布,我们需要设计转移矩阵Q,使得平稳分布q(X)近似等于目标分布P(X) - 对于MCMC来说,我们不需要显示的去寻找一个分布q(x),而是通过构造一个转移矩阵 Q = [ Q i j ] k × k Q=[Q_{ij}]_{k\times k} Q=[Qij]k×k和一个初始的样本 q ( 1 ) ( X ) q^{(1)}(X) q(1)(X),经过若干步骤后就达到平稳分布q(X),但我们不需要知道q(X)的形式.我们只需构造马氏链即可,马氏链必备转移矩阵Q和状态空间 { 1 , 2 , . . . , K } \{1,2,...,K\} {1,2,...,K},那么这个马氏链就可以了。
- 具体采样步骤如下:假定我们已知状态转移矩阵Q,它的状态空间为K个,那么初始的 q ( 1 ) ( X ) q^{(1)}(X) q(1)(X)是一个离散型的概率分布,这个分布我们可以任意给, q ( 1 ) ( X ) q^{(1)}(X) q(1)(X)可以是均匀分布,也可以从1~K中任意的选择一个状态,这是马氏链的本身的性质,
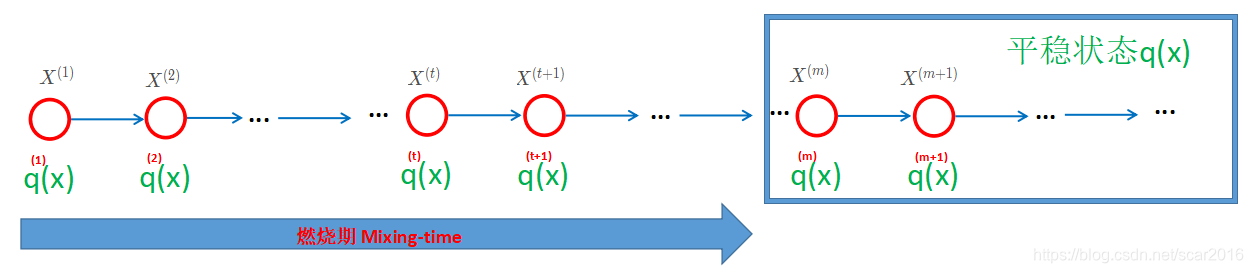
- 马氏链的性质:无论初始状态选择1~K中任意的一个状态,经过有限步骤后,分布会收敛到同一个平稳分布。平稳分布q(X)与状态转移矩阵相关,与初始状态无关
9.1 MCMC问题
- 理论只保证收敛性,但无法知道何时收敛
- 混合时间过长,难以收敛,导致发散;根本原因是P(X)太复杂,维度太高且维度之间有相关性。
- 在平稳分布以后的样本 X ( m ) X^{(m)} X(m)与 X ( m + 1 ) X^{(m+1)} X(m+1)是相关的,即样本之间有一定的相关性,为了解决上述问题,我们应该每隔几步采样。
举例说明:
对于混合高斯模型来说,会有一个什么问题呢?就是样本都趋向于一个峰值附近,很有可能会过不了低谷,导致样本都聚
集在一个峰值附近。这个问题出现的原因我们可以从能量的角度来解释这个问题。在无向图中,我们
常用下列公式来进行表示:
P ( X ) = 1 Z P ^ ( X ) = 1 Z e x p − E ( X ) (29) P(X)=\frac{1}{Z}\hat{P}(X)=\frac{1}{Z}exp^{-E(X)}\tag {29} P(X)=Z1P^(X)=Z1exp−E(X)(29)

实际上这里的 E(X) 指的就是能量函数,能量和概率是成反比的,概率越大意味着能量越低,能量越低,越难发生跳跃的现象。所以,采样很容易陷入到一个峰值附近。并且,多峰还可以分为均匀和陡峭,陡峭的情况中,能量差实在是太大了,就很难发生跳跃。就像孙悟空翻出如来佛祖的五指山一样,佛祖的维度很高,孙悟空在翻跟头的时候,一直在一个低维里面不同的打转,根本就跳不出来,就是来自佛祖的降维打击。所以,在高维情况下,很容易发生在一个峰值附近不停的采样,根本就跳不出来,导致采到的样本的多样性低,样本之间的关联性大,独立性低。
这篇关于23-MCMC-马尔科夫链蒙特卡洛的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!