R 贝叶斯输出分析和诊断MCMC：coda包

本文主要是介绍R 贝叶斯输出分析和诊断MCMC：coda包，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

描述

该文档介绍了R语言中的`coda`包，这是一个用于处理Markov Chain Monte Carlo (MCMC)模拟输出分析和诊断的工具。包提供了函数来总结、绘制MCMC结果，以及进行收敛性诊断测试。

函数总览

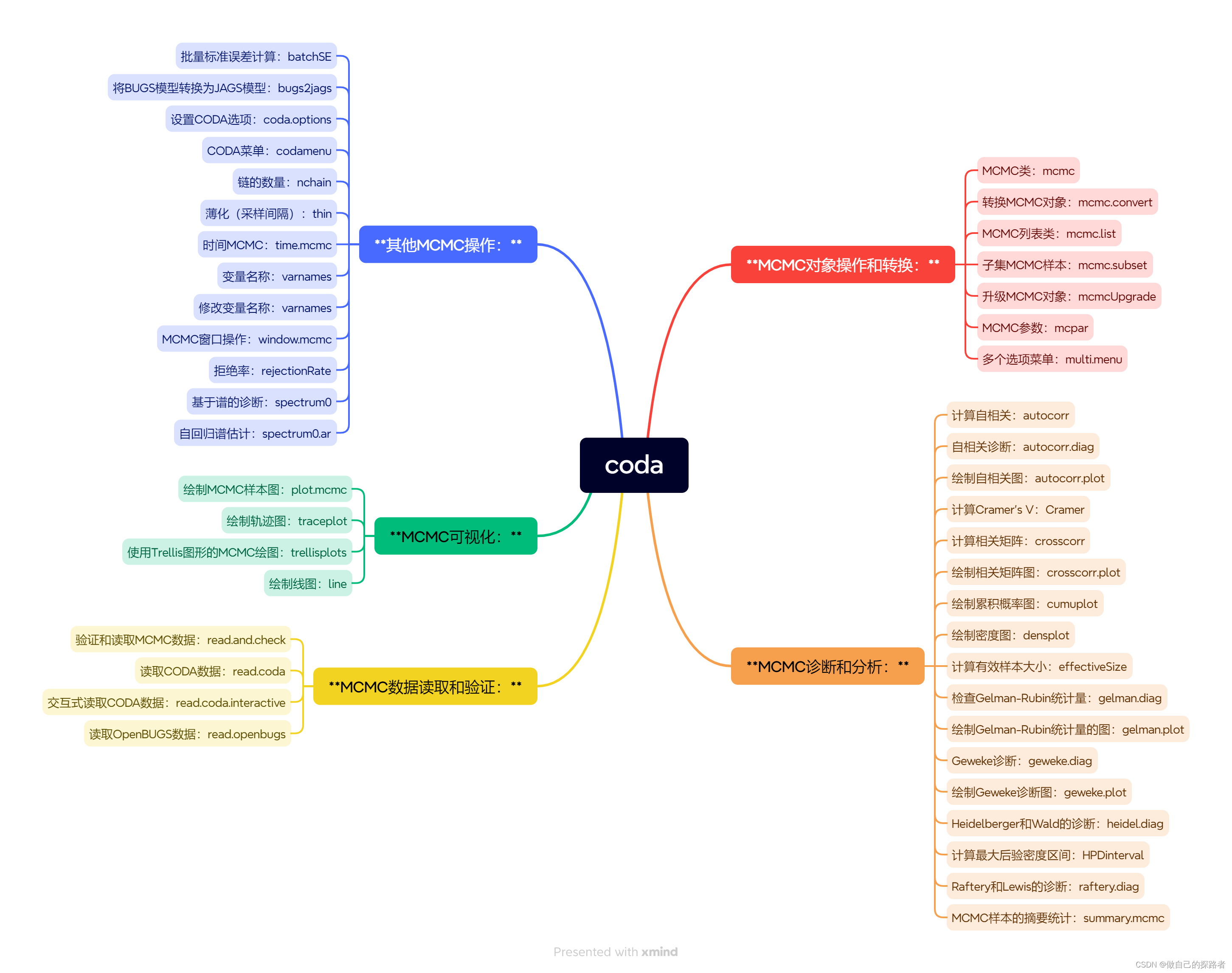数据输入与转换：

bugs2jags: 将BUGS格式的数据转换为JAGS格式。
- bugs2jags(infile, outfile)
read.coda: 读取CODA格式的MCMC输出文件。
- 读取以 OpenBUGS 和 JAGS 生成的 CODA 格式马尔可夫链蒙特卡罗的输出。
- ```
read.coda(output.file, index.file, start, end, thin, quiet=FALSE)read.jags(file = "jags.out", start, end, thin, quiet=FALSE)
```
- 参数：
  - start： First iteration of chain"指的是马尔科夫链中的第一个步骤或循环。在进行Markov链Monte Carlo(MCMC)模拟时，初始的迭代可能没有达到平稳分布，即所谓的“收敛”。Geweke.diag检验用于判断样本的开始部分和结束部分是否来自相同的分布。如果Geweke的Z-score显示不一致，可能需要丢弃开始的若干迭代以检查剩余链是否已收敛。因此，“first iteration of chain”在这里是指可能需要被丢弃的、用于warm-up或适应阶段的初期迭代。
  - end：考虑收敛性时，马尔可夫链中的最终或剩下的一个观测点。
  - thin：链条稀疏间隔（Thinning interval）是指在马尔可夫链蒙特卡洛（MCMC）模拟中，从连续的采样值中选择一个子集时所使用的步长。它决定了在存储或分析结果时，忽略多少个样本点，只保留每`thin`个样本中的一个。例如，`thin=2`意味着保留每个偶数迭代的样本，而丢弃奇数迭代的样本，以此来减少数据量并可能减少样本间的相关性。在R的`mcmc`对象中，`thin`属性给出了两个连续采样值之间的这个间隔。
read.coda.interactive: 交互式读取CODA格式的MCMC输出
- 不需要任何参数。相反，系统会提示用户输入所需的信息

read.openbugs: 读取OpenBUGS的输出文件。

read.openbugs(stem="", start, end, thin, quiet=FALSE)# "<stem>CODAindex.txt", "<stem>CODAchain1.txt", "<stem>CODAchain2.txt",

as.ts.mcmc: 将MCMC对象转换为时间序列格式。

MCMC处理与分析：

mcmc: 创建MCMC对象。
mcmc.list: 创建MCMC列表对象。
mcmc.convert: 转换MCMC对象格式。
mcmc.subset: 子集选择MCMC样本。
mcmcUpgrade: 升级MCMC对象。
thin: 选择MCMC样本的子集（薄化）。
effectiveSize: 用于估计平均值的有效样本量
- 根据自相关调整样本大小。
- 在MCMC模拟中，样本大小通常需要考虑自相关性来估计参数的均值。当时间序列数据存在自相关时，标准误差的计算会受到高估，因为自相关降低了独立观测的数量。调整样本大小（effective sample size）是为了准确估计统计量的不确定性，如均值的标准误差。在存在自相关的情况下，简单地将观测值数量除以方差会导致对估计精度的过高估计。通过调整样本大小，可以更好地反映由于自相关导致的信息损失，从而提供更准确的统计推断。

统计诊断与可视化：

autocorr: 计算自相关。
- 马尔可夫链的自相关函数
- 在 lags 给出的滞后处计算马尔可夫链 mcmc.obj 的自相关函数。
- `relative` 是一个逻辑标志
  - 如果设置为 `TRUE`，则`lags` 参数表示的是相对于马尔科夫链的稀疏间隔的自相关计算。
  - 如果设置为 `FALSE`，`lags` 表示的是迭代次数之间的绝对差异。
autocorr.diag: 自相关图的诊断。
- 与 autocorr 不同，如果 mcmc.obj 有许多参数，它仅计算与其自身的自相关，而不计算互相关。如果 autocorr 返回矩阵，则此函数返回矩阵的对角线。因此，它对于具有许多参数的链更有用，但对于发现参数可能没有那么帮助。
- 如果 mcmc.obj 属于 mcmc.list 类，则返回的向量是所有链的平均自相关
autocorr.plot: 绘制自相关图。
- 绘制马尔可夫链的自相关图
- ```
autocorr.plot(x, lag.max, auto.layout = TRUE, ask, ...)
```
- 参数
  - `x` 是一个马尔可夫链（Markov Chain）对象，通常在统计分析或模拟过程中使用，尤其是贝叶斯分析中。它代表了一组按照马尔可夫性质生成的序列数据。
  - `lag.max` 是一个参数，用于指定计算自相关函数（autocorrelation function, ACF）的最大滞后值。这决定了在图表上显示的自相关性范围，即分析序列中两个点之间最大时间差的自相关。
  - `auto.layout` 是一个布尔参数，如果设置为 `TRUE`，则会为绘图设置自己的布局；否则，将使用现有的布局。这
  - `ask` 参数决定是否在显示每个绘图页之前提示用户。默认情况下，在 R 中，如果 `dev.interactive()` 返回 `TRUE`，或者在 S-PLUS 中，如果 `interactive()` 返回 `TRUE`，那么将会询问用户。这允许用户在查看多页图形时有更多的控制。
batchSE: 批次标准误差计算。
- 总体的有效标准差可产生正确的标准误差。
- ```
batchSE(x, batchSize=100)
```
- 参数
  - x: mcmc 或 mcmc.list 对象
  - batchSize: 每个批次中包含的观测值数量。
gelman.diag: Gelman-Rubin统计量诊断。
gelman.plot: 绘制Gelman-Rubin统计量的图。
geweke.diag: Geweke统计量诊断。
geweke.plot: 绘制Geweke统计量的图。
heidel.diag: Heidelberger和Welch的诊断。
HPDinterval: 计算最高后验密度区间（HPD）
- ```
HPDinterval(obj, prob = 0.95, ...)
```
- prob : 区间 (0,1) 中的数字标量，给出区间的目标概率内容。间隔的标称概率内容是最接近 prob 的 1/nrow(obj) 的倍数。
crosscorr: 计算变量间的交叉相关性。
- crosscorr 计算马尔可夫链蒙特卡罗输出中变量之间的互相关。如果 x 是 mcmc.list，则在计算相关性之前将 x 中的所有链组合起来。
crosscorr.plot: 绘制交叉相关性图。
cumuplot: 累积分布图。
densplot: 密度图。
density: 计算密度。
densityplot.mcmc: 使用Lattice包绘制MCMC的密度图。
- 显示 x 中每个变量的密度估计值图，由密度函数计算得出。对于离散值变量，会生成直方图
plot.mcmc: 绘制MCMC轨迹图。
traceplot: 轨迹图。
spectrum: 计算谱密度。
spectrum0: 估计零时的谱密度
- 通过将 glm 拟合到周期图的低频端来估计频率零处的谱密度。 spectrum0(x)/length(x) 估计平均值(x) 的方差
spectrum0.ar: 使用AR模型估计谱密度。
- 通过拟合自回归模型来估计频率零处的谱密度。 spectrum0(x)/length(x) 估计平均值(x) 的方差。
raftery.diag: Raftery和Lewis的诊断
- raftery.diag 是基于分位数 q 估计精度标准的游程控制诊断。它旨在用于马尔可夫链的短期试运行。计算以概率 p 估计分位数 q 至 +/- r 精度范围内所需的迭代次数。对每个链中的每个变量进行单独的计算。如果数据迭代次数太小，则会打印一条错误消息，指示试运行的最小长度。最小长度是连续样本之间不存在相关性的链所需的样本大小。正自相关会将所需的样本量增加到该最小值以上。还提供了自相关夸大所需样本量的程度的估计值 I（“依赖因子”）。 I 值大于 5 表示自相关性较强，这可能是由于起始值选择不当、后验相关性较高或 MCMC 算法的“粘性”所致。还计算了在链的开头要丢弃的“烧入”迭代的数量。
summary.mcmc: MCMC样本的摘要统计。

其他辅助函数：

coda.options: 设置CODA包的选项。
codamenu: 显示CODA包的菜单
varnames: 获取或设置MCMC变量的名称。
mcpar: 设置MCMC参数。
multi.menu: 多个菜单选项。
nchain: 查看MCMC链的数量。
niter: 通过nchain获取迭代次数。
nvar: 通过nchain获取变量数量。
options: 设置R的全局选项。
print: 打印MCMC对象。
read.and.check: 读取并检查MCMC数据。
- 输入以交互方式读取，并根据参数what、lower、upper 和answer.in 指定的条件进行检查。如果输入不满足所有条件，则会生成相应的错误消息并提示用户提供输入。重复此过程直到输入有效的输入值
rejectionRate: 计算拒绝率。
start: 设置MCMC的起始值。
start.mcmc: 通过time.mcmc设置MCMC的起始时间。
thin.mcmc: 通过time.mcmc进行时间选择的薄化。
time: 获取MCMC运行时间。
time.mcmc: 时间相关的MCMC函数。
window: 窗口选择。
window.mcmc: MCMC对象的窗口选择。
xyplot: 基于Lattice包的散点图。
xyplot.mcmc: 绘制MCMC的散点图。

图形绘制

levelplot.mcmc 即 trellisplots : 使用Lattice包绘制MCMC的水平图，mcmc 对象的网格图
- 这些方法使用在lattice包中实现的Trellis框架来从“mcmc”和“mcmc.list”对象生成节省空间的诊断图。 xyplot 方法生成轨迹图。密度图方法和 qqmath 方法可生成经验密度图和概率图。 levelplot 方法描述了序列的相关性。 acfplot 方法绘制序列中的自相关性。
qqmath.mcmc 即 trellisplots : 绘制MCMC的QQ图。
panel.densityplot: Lattice包中的密度图面板函数。
panel.xyplot: Lattice包中的散点图面板函数。