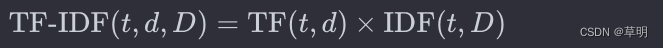inverse专题
CVPR2021-PhySG: Inverse Rendering with Spherical Gaussians for Physics-based Material Editing and Re
作者:Zhang kai + Prof. Noah Snavely Cornell University, Department of Computer Science 光照:natural, static illumination 对象:specular objects 视点:multi-view 相机类型:RGB 时间:no 问题:multi-view inverse render
TF-IDF(Term Frequency-Inverse Document Frequency)
TF-IDF(Term Frequency-Inverse Document Frequency)是一种常用于信息检索和文本挖掘的统计方法,用以评估一个词语对于一个文件集或一个语料库中的其中一份文件的重要程度。它的重要性随着词语在文本中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。TF-IDF算法主要应用于关键词抽取、文档相似度计算和文本挖掘等领域。 以下是TF-IDF算法的
TF-IDF(Term Frequency-Inverse Document Frequency)算法
TF-IDF(Term Frequency-Inverse Document Frequency)是一种用于文本挖掘和信息检索的统计方法,主要用于评估一个单词在一个文档或一组文档中的重要性。它结合了词频(TF)和逆文档频率(IDF)两个指标。以下是详细解释: 1. 词频(TF,Term Frequency) 词频表示一个单词在一个文档中出现的频率。假设我们有一个单词 ( t ) 和一个文档 (
ZOJ 3609 Modular Inverse
Description The modular modular multiplicative inverse of an integer a modulo m is an integer x such that a-1≡x (mod m). This is equivalent toax≡1 (mod m). Input There are multiple test case
Hibernate中cascade和inverse的作用
Inverse和cascade是Hibernate映射中最难掌握的两个属性。两者都在对象的关联操作中发挥作用。1.明确inverse和cascade的作用inverse 决定是否把对对象中集合的改动反映到数据库中,所以inverse只对集合起作用,也就是只对one-to-many或many-to-many有效(因 为只有这两种关联关系包含集合,而one-to-one和many-to-one只含
hibernate进阶之一对多和inverse属性
dept.java package cn.itcast.b_one2Many;import java.util.HashSet;import java.util.Set;public class Dept {private int deptId;private String deptName;// 【一对多】 部门对应的多个员工private Set<Employee> emps = ne
hibernate中cascade与inverse讲解
这两个属性都用于一多对或者多对多的关系中。而inverse特别是用于双向关系,在单向关系中我们并不需要。 Cascade代表是否执行级联操作,Inverse代表是否由己方维护关系。 Cascade: Cascade属性的可能值有 all: 所有情况下均进行关联操作,即save-update和delete。 none: 所有情况下均不进行关联操作。这是默认
Modular Multiplicative Inverse(模乘逆元)
计算模乘逆元原理上有四种方法: 1.暴力算法 2.扩展欧几里得算法 3.费尔马小定理 4.欧拉定理 模乘逆元定义:满足 ab≡1(mod m),称b为a模乘逆元。以下是有关概念以及四种方法及程序。 文章出处:Modular Multiplicative Inverse The modular multiplicative inverse of an integer a modu
CCD IK (Inverse Kinematics) 的说明
http://www.ryanjuckett.com/programming/animation/21-cyclic-coordinate-descent-in-2d
NHibernate之 inverse
(原文链接 http://ddbiz.com/?p=219)NHibernate中的集合(collections)描述了不同的关联映射方式,如one-to-many, many-to-one, many-to-many等, collections的 hbm定义中, inverse="true|false" 表明了变化的信息由哪一端来保存
C#,数值计算,矩阵的行列式(Determinant)、伴随矩阵(Adjoint)与逆矩阵(Inverse)的算法与源代码
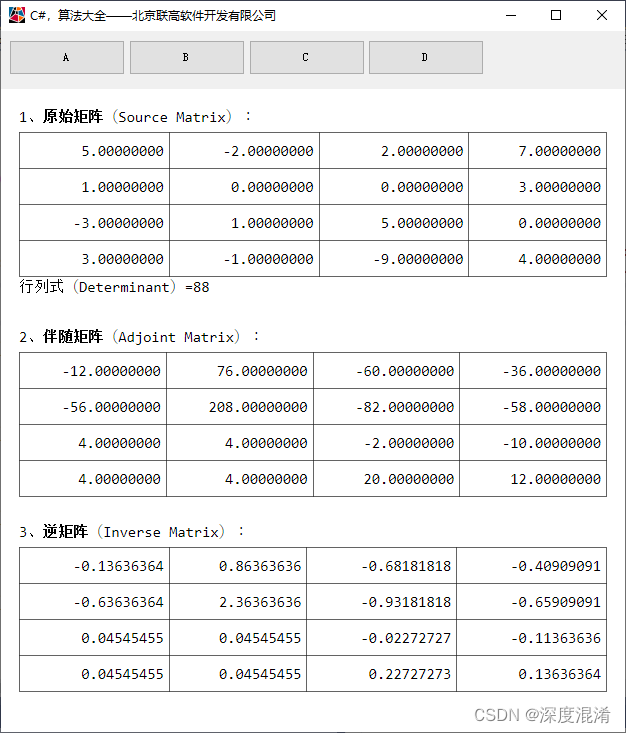
本文发布矩阵(Matrix)的一些初级算法。 一、矩阵的行列式(Determinant) 矩阵行列式是指矩阵的全部元素构成的行列式,设A=(a)是数域P上的一个n阶矩阵,则所有A=(a)中的元素组成的行列式称为矩阵A的行列式,记为|A|或det(A)。若A,B是数域P上的两个n阶矩阵,k是P中的任一个数,则|AB|=|A||B|,|kA|=kⁿ|A|,|A*|=|A|,其中A*是A
poj 2429 GCD LCM Inverse
http://poj.org/problem?id=2429 这题能1A感觉很好!Pollard_Rho 很神奇呀,能把这么大的数分解成素因子,然后dfs 找到其 ,lcm/gcd 的所有的因子就行了,取最优的答案 #include<iostream>#include<cstdio>#include<ctime>#include<cstring>#include<cstdlib>
Inverse Optimization: Theory and Applications
一、介绍逆优化问题基本概念 传统优化问题是给定目标函数和约束,求最优决策。而逆优化问题是给定一组决策,求使这组决策成为最优决策的目标函数和/或约束条件。两类问题的思路正好相反。 传统优化问题由下述组成: 决策变量空间X目标函数f(x),用于衡量不同决策的优劣约束集g(x)≤0,限制决策选择范围目标是求解min f(x),使其满足约束条件得到最优决策x* 而逆优化问题给出的是一个组决策{xi
线性代数学习笔记二:可逆矩阵inverse matrix
逆矩阵(方阵) 如果存在使得,则A是可逆的、非奇异的,且使得=。 逆矩阵的概念类似于数学中的导数,5*(1/5)=1,,矩阵A的“倒数”是它的逆矩阵。 逆矩阵产生的原因: 用来实现矩阵的除法。比如有矩阵X,A,B,其中X*A = B,我们要求X矩阵的值。本能
TF-IDF(Term Frequency-Inverse Document Frequency)算法 简介
TF-IDF(Term Frequency-Inverse Document Frequency)是一种用于信息检索和文本挖掘的常用算法。它用于评估一个词对于一个文档集合中某个文档的重要性。 这个算法的基本思想是:如果一个词在一个文档中频繁出现,并且在整个文档集合中很少出现,那么这个词对于这个文档的重要性较高。TF-IDF的计算涉及两个部分:词频(TF)和逆文档频率(IDF)。 1. 词频(T
Hibernate关系关联中inverse(反转)和cascade(级联)操作
http://c.biancheng.net/view/4207.html(源网址) 在 Hibernate 的关联关系中,可以使用单向关联关系,也可以使用双向关联关系,在双向关联关系中,Hibernate 会同时控制双方的关系,这样在程序操作时,很容易出现重复操作的问题。 为了解决这一问题,Hibernate 提供了反转操作,同时,为了在操作多表时,主表(主控方)操作后的数据能与关联表的数据保
Hibernate集合映射中的inverse属性以及cascade级联
Inverse属性 Inverse属性,是在维护关联关系的时候起作用的。 表示控制权是否转移。(在一的一方起作用) Inverse , 控制反转。 Inverse = false 不反转; 当前方有控制权 True 控制反转; 当前方没有控制权 只在集合映射中才能使用。 注意:<one-to-many /> 和<many-to-one
MATLAB - 机器人逆运动学设计器(Inverse Kinematics Designer APP)
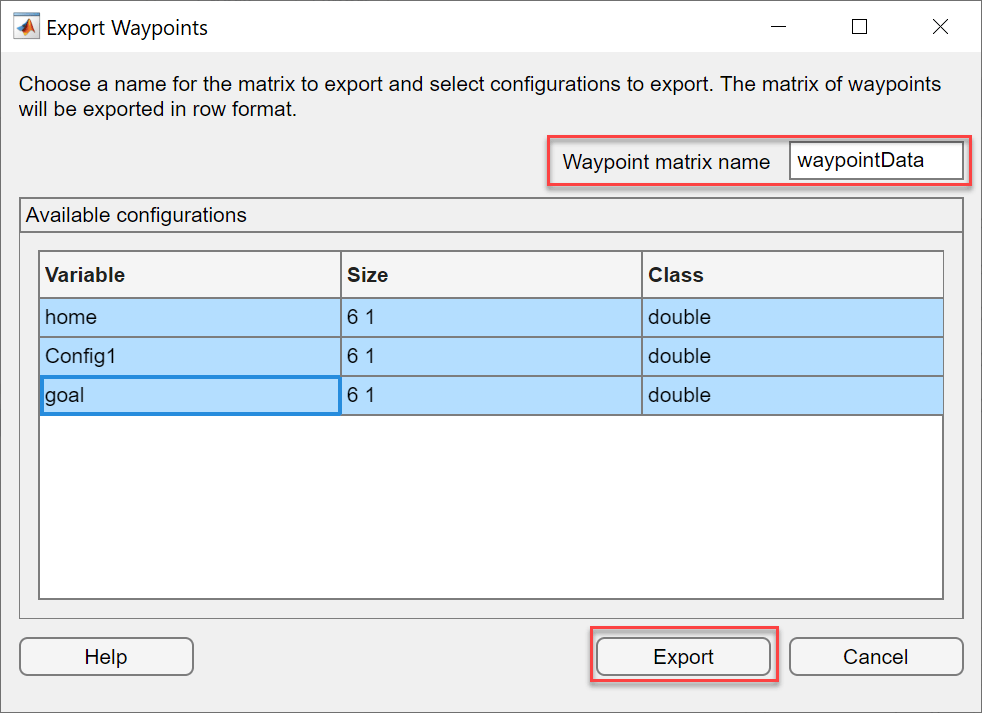
系列文章目录 前言 一、简介 通过逆运动学设计器,您可以为 URDF 机器人模型设计逆运动学求解器。您可以调整逆运动学求解器并添加约束条件,以实现所需的行为。使用该程序,您可以 从 URDF 文件或 MATLAB 工作区导入 URDF 机器人模型。调整逆运动学求解器和约束条件。创建关节配置并导出航点。将求解器设置、约束和关节配置导出到 MATLAB® 工作区。 二、打
MATLAB - 机器人逆运动学设计器(Inverse Kinematics Designer APP)
系列文章目录 前言 一、简介 通过逆运动学设计器,您可以为 URDF 机器人模型设计逆运动学求解器。您可以调整逆运动学求解器并添加约束条件,以实现所需的行为。使用该程序,您可以 从 URDF 文件或 MATLAB 工作区导入 URDF 机器人模型。调整逆运动学求解器和约束条件。创建关节配置并导出航点。将求解器设置、约束和关节配置导出到 MATLAB® 工作区。 二、打
创宇区块链|Inverse Finance 安全事件分析
前言 北京时间 2022 年 4 月 2 日晚,Inverse Finance 借贷协议遭到攻击,损失约 1560 万美元。知道创宇区块链安全实验室第一时间跟踪本次事件并分析。 分析 基础信息 攻击tx1:0x20a6dcff06a791a7f8be9f423053ce8caee3f9eecc31df32445fc98d4ccd8365 攻击tx2:0x600373f67521324c8
【刷题】Modular Multiplicative Inverse 模逆元
模逆元 定义 整数 a a a的模逆元是满足 a ⋅ x a\cdot x a⋅x模一个模数 m m m等于1。也就是找到一个数 x x x: a ⋅ x ≡ 1 mod m. a \cdot x \equiv 1 \text{ ~~~~mod m.} a⋅x≡1 mod m. 也可以把 x x x表示为 a − 1 a^{-1} a−1 需要注意模逆并不是总是存在。例如, m =
Parallel Diffusion Models of Operator and Image for Blind Inverse Problems
盲逆问题算子和图像的并行扩散模型 论文链接:https://arxiv.org/abs/2211.10656 项目链接:https://github.com/BlindDPS/blind-dps Abstract 在正向算子已知的情况下(即非盲),基于扩散模型的逆问题求解器已经展示了最先进的性能。然而,该方法对盲逆问题的适用性还有待探索。 在这项工作中,我们证明我们确实可以通过为前向算
在hibernate中一对多关联时会经常用到inverse和cascade属性
原文网址:http://hi.baidu.com/icehua521/blog/item/eb6b5099a98271006e068cbf.html 在hibernate中一对多关联时会经常用到inverse和cascade属性 , inverse 有两个值 true ,false,默认值是false ;如果设置为true 则表示对象的状态变化不会同步到数据库 ;设置false就相反拉;
TF-IDF Term frequency - inverse document frequency
关键字提取算法之TF-IDF扫盲 TF-IDF(term frequency–inverse document frequency)是一种用于资讯检索与资讯探勘的常用加权技术。TF-IDF是一种统计方法,用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随著它在文件中出现的次数成正比增加,但同时会随著它在语料库中出现的频率成反比下降。TF-IDF加权的
浅谈hibernate(cascade,lazy,inverse,fetch)
1.cascade是否执行级联操作 <set name="children" lazy="true" cascade="all"> 在保存主表的时候,如果没有保存从表信息,会抛出异常,如果设置了级联关系,可以自动先保存从表,在保存主表 all: 所有情况下均进行关联操作,即save-update和delete。 none: 所有
Inverse Factorial
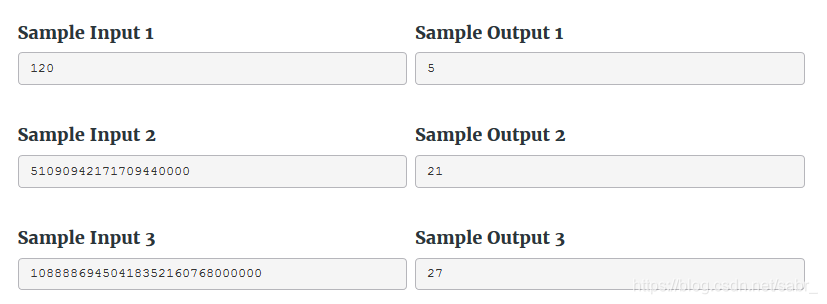
题目意思就是已知n的阶乘,求n。 当输入的阶乘小于10位数的时候,我们可以用long long将字符串转化成数字,直接计算。 而当输入的阶乘很大的时候,我们就可以利用位数去大概的估计n。 #include <bits/stdc++.h>using namespace std;typedef long long ll;ll n, m, num, res, ans, len;strin