Inverse Factorial

本文主要是介绍Inverse Factorial，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

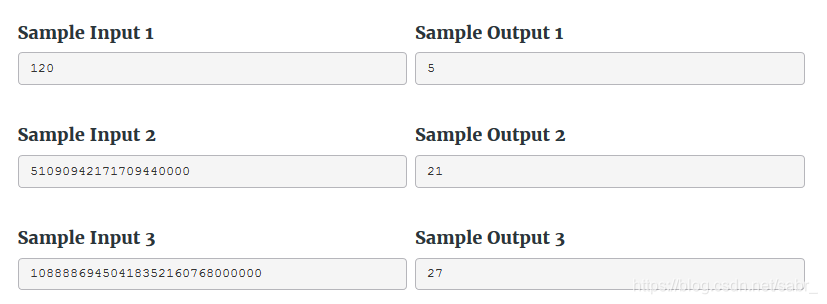
题目意思就是已知n的阶乘，求n。

当输入的阶乘小于10位数的时候，我们可以用long long将字符串转化成数字，直接计算。

而当输入的阶乘很大的时候，我们就可以利用位数去大概的估计n。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n, m, num, res, ans, len;string str;
void input() {cin >> str;len = str.size();if( len < 10 ) {ll i = 1;ll ans = 1;while( true ) {ans *= i;if( ans == atoi(str.c_str()) ) {cout << i;break;}i ++;}} else {ll i = 1;double ans = 1;while( true ) {ans += log10(i);if( floor(ans)==len ) {cout << i;break;}i ++;}}
}int main(){input();return 0;
}

转载于：https://www.cnblogs.com/Asimple/p/6768496.html

这篇关于Inverse Factorial的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---