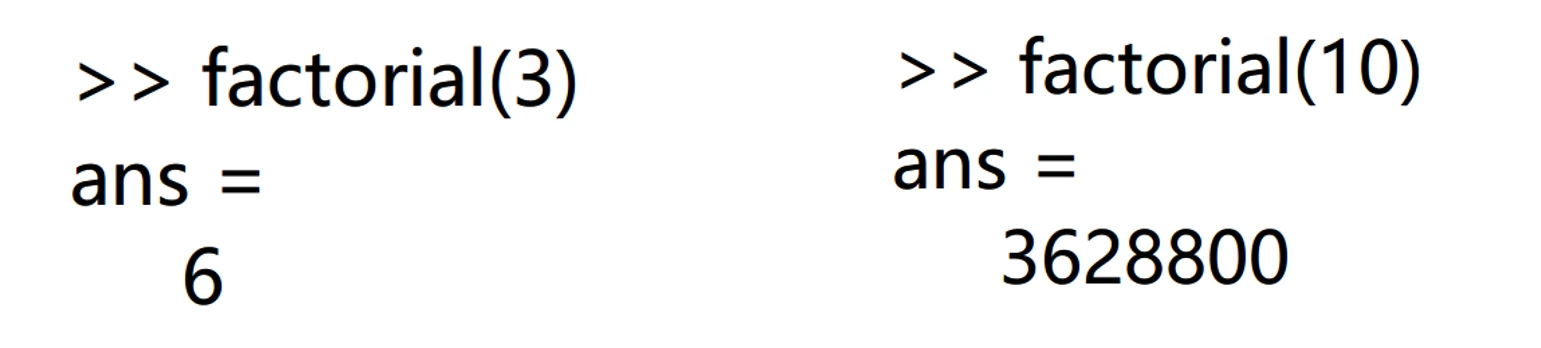factorial专题
【数学】 HDU 1124 Factorial
链接:XXXXX 题目看起来 好长 涉及题意的就是那么几句话。。。有必要酱子么。 #include <iostream>#include <cstdio>#include <cstring>#include <algorithm>#include <cmath>using namespace std;int main(){int st[] = {5,25,125,625,312
zoj 4745 Factorial Problem in Base K
题目链接:点击打开链接 题目的意思就是:给一个k进制的数s,求s!在10 进制下的末尾0个数。 思路: 先把s转化为10进制下的数。 把n!分解质因数。 把k分解质因数。 求所有的k的质因数中,除以n!的相同质因数中最小的。就是answer。 例如: 看这组数据:10 10. s本来就是10进制下的。所以不用转化。 10!=2^8*3^4*5^2*7 10=2*5; 看10
[LeetCode] 172. Factorial Trailing Zeroes
题目内容 给定一个整数 n,返回 n! 结果尾数中零的数量。 示例 1:输入: 3输出: 0解释: 3! = 6, 尾数中没有零。示例 2:输入: 5输出: 1解释: 5! = 120, 尾数中有 1 个零. 题目思路 需要思考一下,到底什么情况下会出现0。那么根据经验,只要碰到包含因子5的数字,就会出现0.(包含5然后包含偶数,而且偶数的数量大于5的个数)。比如5!包含1个
《leetCode》:Factorial Trailing Zeroes
题目 Given an integer n, return the number of trailing zeroes in n!.Note: Your solution should be in logarithmic time complexity. 思路一:不能AC 思路,统计2和5的个数 ,时间复杂度为O(n) int min(int a,int b){return a<b?a:
LeetCode(31)-Factorial Trailing Zeroes
题目: Given an integer n, return the number of trailing zeroes in n!.Note: Your solution should be in logarithmic time complexity. 思路: 题意是要求一个数字的阶乘,末尾有多少个0要求是对数级别的时间,所以考虑用递归分析一下,产生一个10,后面加0,找到所有的2*5,
LeetCode--172. Factorial Trailing Zeroes
Problem: Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. Analysis: 对n!做质因数分解n!=2x*3y*5z*… 显然0的个数等于min(x,z),并且min(x,z
解决使用statsmodels导包时报ImportError: cannot import name 'factorial'的问题。
在使用的过程中,发现使用 import statsmodels.api as sm时,会报找不到factorial模块的问题。 可以看得出是依赖了scipy这个库的一个misc模块,但是由于最新版本的scipy中,scipy.misc 已经迁移到 scipy.special 里面了。目前我用的python版本是3.6。其中statsmodels(0.9.0)和 scipy(1.3.0)
LeetCode题解——Factorial Trailing Zeroes
Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. 出现0的情况是,出现5和2的倍数。 [n/k]代表1~n中能被k整除的个数,而能被2整除的个数多余能被5整除的个数,故只要知
Project Euler_Problem 160_Factorial Trailing Digits_费马小定理,威尔逊定理,左右互搏
原题目: 题目大意:1e12的阶乘,不算末尾的0,后5位数字为多少 解题思路: 暴力运算也能算,就是有点慢,优化过后可能也得算个几十分钟 这里考虑使用威尔逊定理+费马小定理 用这个方法我们就可以得到对于任何一个小于p的数n,p为素数,n!在模p下的结果, 对于本题: 则我们要找的答案应该是512628437919+k*39的最后几位有效数字,当k>100000时,显然末尾数字就
Project Euler 题解 #20 Factorial digit sum
题目:Factorial digit sum n! means n (n 1) ... 3 2 1 For example, 10! = 10 9 ... 3 2 1 = 3628800, and the sum of the digits in the number 10! is 3 + 6 + 2 + 8 + 8 + 0 + 0 = 27. Find the sum of the di
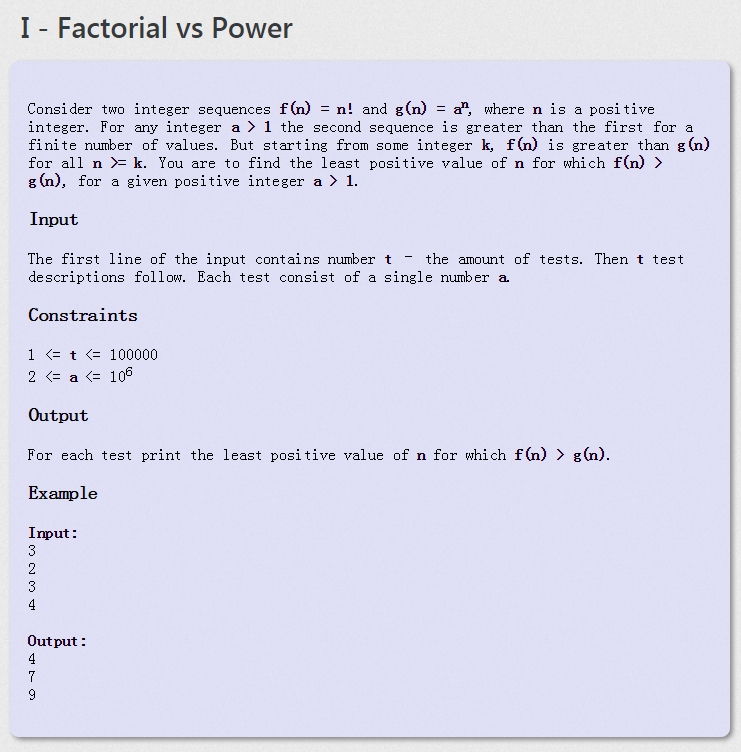
ACM 斯特林公式 Factorial vs Power
斯特林公式(Stirling's approximation)是一条用来取n的阶乘的近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特林公式十分好用,而且,即使在n很小的时候,斯特林公式的取值已经十分准确。 SPOJ Factorial vs Power 题目大意:对于给定的a,求满足的 n! > an 最小的n。 思路:利用斯特林公式,可以代替到n!
LeetCode Factorial Trailing Zeroes数学方法详解
Given an integer n, return the number of trailing zeroes in n!. 题目的意思是要求一个整数的阶乘末尾有多少个0; 1.需要注意的是后缀0是由2,5相乘得来,因此只需看有多少个2,5即可 n = 5: 5!的质因子中 (2 * 2 * 2 * 3 * 5)包含一个5和三个2。因而后缀0的个数是1。 n = 11: 11!的质因子中
【HDU】 1124 Factorial
Factorial 题目链接 Factorial 题目大意 题目扯了一大堆没用的,最后说让你求 N! N!末尾有多少零。 题解 末尾想产生零只有可能是2*5,所以我们找出min(num2,num5)就行了。 然而很明显2的数量肯定比5多,所以我们这里只用求5的数量就行了,所以我们用N整除5,25,125….最后加进答案中就行了。 代码 #
[LeetCode]172.Factorial Trailing Zeroes
题目 Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. 分析 朴素解法: 首先求出n!,然后计算末尾0的个数。(重复÷10,直到余数非0) 该解法在输入的数字稍大时就会导致阶乘得数溢出,
[Leetcode]172. Factorial Trailing Zeroes
Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. 我们对n!分解质因子,n!=2^x+3^y+5^z+...,结尾的0一定是1个2和1个5相乘得到的。很显然,这里因子5的个数小于因子2的个
MATLAB知识点:factorial函数(★★★☆☆)计算阶乘
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。 MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili 节选自第3章:课后习题讲解中拓展的函数 在讲解第三章课后习题的过程中,我给大家拓展了一些讲义中没有介绍的新函数: (5)factorial函数(★★★☆☆) factorial函数用于计算阶乘
洛谷10月月赛R1T1-SAC E#1 - 一道中档题 Factorial(pollard-rho质因数分解)
传送门 小数据做法(改了之后):http://blog.csdn.net/stone41123/article/details/78172763 大数据做法(没改之前的数据范围): 我们沿用之前的做法,只是质因数分解如果再用 O(n√) O(\sqrt n)的,那么就会TLE 我们可以使用pollard-rho质因数分解,听说时间是 O(n14) O(n^{\frac 1 4})的,我自己
洛谷10月月赛R1-T1-一道中档题 Factorial
传送门 首先,我们可以这样分解阶乘质因数: cnt(p)=∑i=1∞⌊npi⌋ cnt(p)=\sum_{i=1}^{\infty} \big\lfloor {\frac n {p^i}}\big\rfloor 也就是枚举质数一直除,具体原理可以自己想,我不多说。 对于这个题,大家应该有些人做过这个题的简单版本吧: 求n!末尾0的个数。 这个题的做法还是很简单的,用
light-1045 - Digits of Factorial【思维】(数学)
题目链接:点击打开链接 1045 - Digits of Factorial PDF (English)StatisticsForum Time Limit: 2 second(s)Memory Limit: 32 MB Factorial of an integer is defined by the following function f(0) = 1
整数的阶乘(英语:factorial)是所有小于及等于
整数的阶乘(英语:factorial)是所有小于及等于该数的正整数的积,0的阶乘为1。即:n!=1×2×3×...×n。 实例 #!/usr/bin/python3 # Filename : test.py # author by : www.dida100.com # 通过用户输入数字计算阶乘 # 获取用户输入的数字 num = int(input("请输入一
Leetcode#172. Factorial Trailing Zeroes
题目描述:给定一个整数 n,计算 n! 末尾有多少个0 解题思路:虽然代码只有短短几行,但问题的解决是需要技巧的。 首先明确一个问题,n! 末尾若有0出现,那么一定是 2 * 5得来的,所以如果我们知道了 n! 中有多少个 2 * 5,那么就知道了末尾有多少个0;接下来,我们就想一想n! 中有多少个 2 * 5?有一个事实,在 n! 中,2的个数一定是大于5的个数的,有博主给出了证明,如下:
ZOJ Monthly, June 2012 - K Factorial Problem in Base K - zoj 3621
本场比赛,相对最好做的一题,看出本质,就容易了。 问题简化下,比如给你十进制数 s, 问 s! 末尾有几个0。我们一般都是直接找有多少个 2,5。因为2*5 = 10 那么 现在是 k进制数 s, 同理,就是找 s! 里面,有多少个因子的能够组成 k,最多组成 ans 个 k, ans 就是答案。 这个 自己可以简单证明下。后面好处理。 View Code 1 #include<cs
leetcode 172. Factorial Trailing Zeroes求后面0的个数
Given an integer n, return the number of trailing zeroes in n!. Example 1: Input: 3Output: 0Explanation: 3! = 6, no trailing zero. Example 2: Input: 5Output: 1Explanation: 5! = 120, one traili
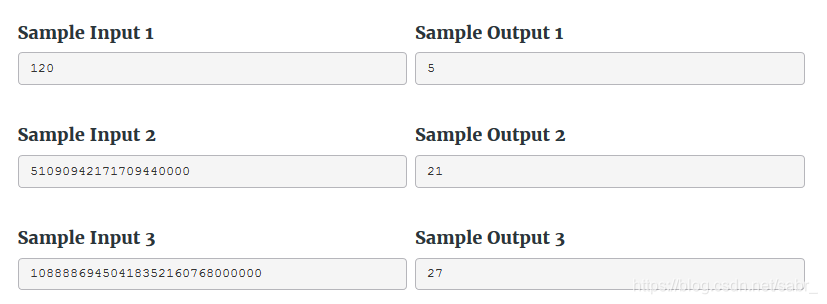
Inverse Factorial
题目意思就是已知n的阶乘,求n。 当输入的阶乘小于10位数的时候,我们可以用long long将字符串转化成数字,直接计算。 而当输入的阶乘很大的时候,我们就可以利用位数去大概的估计n。 #include <bits/stdc++.h>using namespace std;typedef long long ll;ll n, m, num, res, ans, len;strin
【E:Faulty Factorial】(数论,循环节)
**链接**:http://sua2018.contest.codeforces.com/group/J1GbXiu37w/contest/227105 **题意**:在1*2*3*......*n中改变一个数为比它小的数,使得%p等于r.输出任意一个解 2<=n&&n<=1e18 2<=p&&p<1e7 **分析**:n很大,从p入手,考虑循环节。但是真的很暴力 看代码: #prag




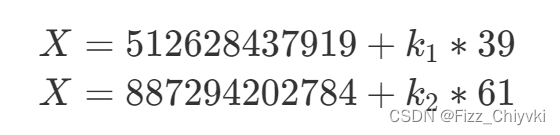

![[LeetCode]172.Factorial Trailing Zeroes](https://img-blog.csdn.net/20150207203556051)