hanoi专题
Codeforces 392B Tower of Hanoi(递归+记忆化搜索)
题目链接:Codeforces 392B Tower of Hanoi 题目大意:给出一个3*3的矩阵,表示从i移动到j的代价,现在给出n,表示有n个碟子在1柱,需要移动到3柱,要求给出最小的花费。 解题思路:dp[l][r][n],表示的是从l移动n个碟子到r的最小花费,然后总共有两种移动方式: ans1 = solve(l, x, n-1) + solve(x, r, n-1
Codeforces Round #230 (Div. 2) C. Blocked Points D. Tower of Hanoi
C. Blocked Points 题意:A点和B点是4-connected,的条件是 the Euclidean distance between A and B is one unit and neither A nor B is blocked; or there is some integral point C, such that A is 4-connected with C,
poj1920 Towers of Hanoi
关于汉诺塔的递归,记住一个结论是,转移n个盘子至少需要2^n-1步 #include<iostream>#include<cstdio>#include<cmath>#include<cstring>#include<algorithm>#include<string>using namespace std;int two[100005],pos[100005];int m
227.Mock Hanoi Tower by Stacks-用栈模拟汉诺塔问题(容易题)
用栈模拟汉诺塔问题 题目 在经典的汉诺塔问题中,有 3 个塔和 N 个可用来堆砌成塔的不同大小的盘子。要求盘子必须按照从小到大的顺序从上往下堆 (如,任意一个盘子,其必须堆在比它大的盘子上面)。同时,你必须满足以下限制条件: (1) 每次只能移动一个盘子。 (2) 每个盘子从堆的顶部被移动后,只能置放于下一个堆中。 (3) 每个盘子只能放在比它大的盘子上面。 请写一段程序,实现将第一个堆
【2016-2017 ACM-ICPC (ECNA 2016) G】That's One Hanoi-ed Teacher(思维)
题目链接:http://codeforces.com/gym/101196 题目大意:询问当前状态是否是最优方案中的一种,若是输出剩下还需多少步 题目思路: 汉诺塔的递归函数的写法是 dfs(a,c,b) dfs(b,a,c) 分别是在a以c为辅助去b,在b以a为辅助去c 所以其实它呈现出的是一个二叉树的结构 首先根据汉诺塔的性质,最大的环要么在第一个柱子,要么在第三个
递归学习简单的小例子之hanoi塔问题
汉诺塔大家早就很熟悉了,今天重新学习一下是出于加深递归思想的目的,之前接触递归的时候老师都是以斐波那契数列或者阶乘、汉诺塔问题来说明讲解的,但是这样形式化的讲解却不见得真的能明白递归的思想,我就是一个例子,到现在做题的时候才意识到弄明白这个思想多重要,现在重新学习也希望为时不晚,好了不说这些了,下面是简单的实现: #!usr/bin/env python#encoding:u
汉诺塔问题(Hanoi问题)的递归算法与非递归算法详解
递归算法分析如下, 设A上有n个盘子。 如果n=1,则将圆盘从A直接移动到C。如果n=2,则:(1)将A上的n-1(等于1)个圆盘移到B上;(2)再将A上的一个圆盘移到C上;(3)最后将B上的n-1(等于1)个圆盘移到C上。如果n=3,则:A)将A上的n-1(等于2,令其为n`)个圆盘移到B(借助于C),步骤如下:(1)将A上的n`-1(等于1)个圆盘移到C上。(2)将A上的一个圆盘移到B
c语言10个盘子,汉诺塔问题,当盘子个数为10时,hanoi函数一共被调用了几次?...
满意答案 指为武义人民 2020.04.09 采纳率:56% 等级:7 已帮助:259人 1023 可以设一个计数器 代码: #include "stdafx.h" #include using namespace std; int pp = 0; void move(char src, char dest) { cout << src << "-->" << dest << end
SSL-ZYC Hanoi双塔问题
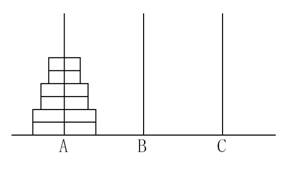
题目大意: 给定A,B,C三根足够长的细柱,在A柱上放有2n个中间有空的圆盘,共有n个不同的尺寸,每个尺寸都有两个相同的圆盘,注意这两个圆盘是不加区分的(下图为n=3的情形)。现要将 这些国盘移到C柱上,在移动过程中可放在B柱上暂存。要求: (1)每次只能移动一个圆盘; (2) A、B、C三根细柱上的圆盘都要保持上小下大的顺序; 任务:设An为2n个圆盘完成上述任务所需的最少移动次数,
【动态规划】POJ_1958 Strange Towers of Hanoi
题意 输出n个盘子在4个塔的汉诺塔问题最少要多少步。 思路 我们设f[n]为n个盘子在4塔的汉诺塔问题下需要的最少步数,d[i]为i个盘子在3塔的汉诺塔问题下需要的最少步数,可以得出动态转移方程: f[n]=min(2∗f[i]+d[n−i]) f [ n ] = m i n ( 2 ∗ f [ i ] + d [ n − i ] ) f[n]=min(2*f[i]+d[n-i])
实验一:求整数和、铺地板和Hanoi塔等问题的求解
实验一:求整数和、铺地板和Hanoi塔等问题的求解 一、问题描述 整数求和: 从1到n之间的整数相加,和是多少? 用C语言实现函数,输入n,返回和;铺地板问题: 在2×n的矩形中铺入1×2大小的地板,求其有多少种铺法;Hanoi塔问题: 一次只能移动一层,大的不能放在小的上面。可以使用临时场所 暂存中间结果。移动n层的塔,总的移动次数是多少?; 二、实验描述 用C语言编程实现求整数平方和、
Tower of Hanoi
一本日文数据结构书上看到的 用了递归 代码如下‘ #include <stdio.h>void TowerOfHanoi(int disk, char from, char via, char to){if (disk==1){printf("円盤: %d を%cから%cへ移動する\n", disk, from, to);}else{TowerOfHanoi(disk-1, from,
汉诺塔实现(含数组修改)Implement of hanoi
汉诺塔的实现,包含伪代码,以及输出流程版本和修改数组版本。 #include <iostream>using namespace std;void hanoiPseudocode(int n, char A, char B, char C){如果是一个盘子直接将盘子从A移到C;否则将 n-1个盘子借助C移到B;直接将盘子从A移到C;将B上的n-1个盘子借助A移到C;}void hano
Hanoi 双塔问题
Hanoi 双塔问题 \operatorname{Hanoi\ 双塔问题} Hanoi 双塔问题 题目链接: luogu P1096 \operatorname{luogu\ P1096} luogu P1096 题目 给定 A A A 、 B B B 、 C C C 三根足够长的细柱,在 A A A 柱上放有 2 n 2n 2n 个中间有孔的圆盘,共有 n n n 个
常见算法-汉诺塔(Hanoi)
常见算法-汉诺塔(Hanoi) 1、说明 河内之塔(Towers of Hanoi)是法国人M.Claus(Lucas)于1883年从泰国带至法国的,河内为越战时北越的首都,即现在的胡志明市;1883年法国数学家 Edouard Lucas曾提及这个故事,据说创世纪时Benares有一座波罗教塔,是由三支钻石棒(Pag)所支撑,开始时神在第一根棒上放置64个由上至下依由小 至大排列的金盘(D