Hanoi 双塔问题

$$\mathrm{H}\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{i}双塔问题$$

题目链接：$\mathrm{l}\mathrm{u}\mathrm{o}\mathrm{g}\mathrm{u}\mathrm{P}1096$

题目

给定 $A$ 、 $B$ 、 $C$ 三根足够长的细柱，在 $A$ 柱上放有 $2n$ 个中间有孔的圆盘，共有 $n$ 个不同的尺寸，每个尺寸都有两个相同的圆盘，注意这两个圆盘是不加区分的（下图为 $n=3$ 的情形）。

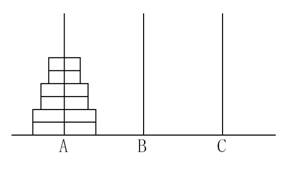
现要将这些圆盘移到 $C$ 柱上，在移动过程中可放在 $B$ 柱上暂存。要求：

（1）每次只能移动一个圆盘；

（2） $A$ 、 $B$ 、 $C$ 三根细柱上的圆盘都要保持上小下大的顺序；

任务：设 $A_n$ 为 $2n$ 个圆盘完成上述任务所需的最少移动次数，对于输入的 $n$ ，输出 $A_n$ 。

输入

一个正整数 $n$ ，表示在 $A$ 柱上放有 $2n$ 个圆盘。

输出

一个正整数, 为完成上述任务所需的最少移动次数 $A_n$ 。

样例输入1

1

样例输出1

2

样例输入2

2

样例输出2

6

数据范围

对于 $50\%$ 的数据， $1\le n\le 25$

对于 $100\%$ 的数据， $1\le n\le 200$

提示

设法建立 $A_n$ 与 $A_{n-1}$ 的递推关系式。

思路

这道题就是普通 dp 加普通高精。

我们可以知道，汉诺塔就是 $f[i]=f[i-1]\ast 2+1$ ，那每个地方多了一个相同的圆盘，那其实可以把这两个圆盘看成一个，然后原来的移动一次就是这里的移动两次。（因为两个盘子都要移动）
那就是在输出之前在把答案乘二再输出。

（不会吧不会吧，不会真有人不知道要用高精吧）

代码

#include<cstdio>
#define ll long longusing namespace std;ll n, f[201][10001], ans[10001];int main() {scanf("%lld", &n);//读入f[1][0] = 1;//初始化f[1][1] = 1;for (int i = 2; i <= n; i++) {f[i][0] = f[i - 1][0];//高精乘2for (int j = 1; j <= f[i][0]; j++)f[i][j] = f[i - 1][j] * 2;f[i][1]++;//加上1for (int j = 1; j <= f[i][0]; j++) {f[i][j + 1] += f[i][j] / 10;f[i][j] %= 10;}while (f[i][f[i][0] + 1]) {f[i][0]++;f[i][f[i][0] + 1] += f[i][f[i][0]] / 10;f[i][f[i][0]] %= 10;}}ans[0] = f[n][0];//高精乘2for (int j = 1; j <= ans[0]; j++)ans[j] = f[n][j] * 2;for (int j = 1; j <= ans[0]; j++) {ans[j + 1] += ans[j] / 10;ans[j] %= 10;}while (ans[ans[0] + 1]) {ans[0]++;ans[ans[0] + 1] += ans[ans[0]] / 10;ans[ans[0]] %= 10;}for (int i = ans[0]; i >= 1; i--)//输出printf("%d", ans[i]);return 0;
}