实验一：求整数和、铺地板和Hanoi塔等问题的求解

实验一：求整数和、铺地板和Hanoi塔等问题的求解

一、问题描述

1. 整数求和： 从1到n之间的整数相加，和是多少？ 用C语言实现函数，输入n，返回和；
2. 铺地板问题： 在2×n的矩形中铺入1×2大小的地板，求其有多少种铺法；
3. Hanoi塔问题： 一次只能移动一层，大的不能放在小的上面。可以使用临时场所 暂存中间结果。移动n层的塔，总的移动次数是多少？；

二、实验描述

1. 用C语言编程实现求整数平方和、铺地板和Hanoi等问题的求解；
2. 在程序中加入clock()来计算求解时间；
3. 使用不同的输入值得到对应的时间值；
4. 分析算法的时间复杂度并与测量结果比较；
5. 如果存在差异，分析原因；

三、实验设计

1. 求整数平方和问题：
   迭代：
   1） 定义函数sum(int n),利用for循环迭代求解前n项整数平方和
   2） 在main函数中定义int型变量j，通过for循环，以j*100作为参数调用sum函数，让j递增，依次计算前1000、2000、3000，…10000的平方和
   3） 定义clock_t类型变量start_time和end_time，调用clock()函数来记录函数开始和结束的执行时间
   4） 打印(double)(end_time-start_time)
   5） 重复5次实验，取平均值
   6） 记录实验数据并绘制Excel图表
2. 铺地板问题：
   1） 定义函数flour(int n),设定n=1与n=2时的基准情形(flour(1)=1,flour(2)=2)，利用递归式flour(n)=flour(n-1)+flour(n-2)求解铺地板的铺法
   2）在main函数中定义int型变量j，通过for循环，以j作为参数调用flour函数，让j递增，依次计算n为30、40、50，…39的铺法
   3）定义clock_t类型变量start_time和end_time，调用clock()函数来记录函数开始和结束的执行时间
   4）打印(double)(end_time-start_time)
   5）重复5次实验，取平均值
   6）记录实验数据并绘制图表
   3．Hanoi塔问题：
   1）定义函数HanoiTower(int n,char source,char, temp,char target)，设定n=1时为基准情形,利用递归式S(n)=2*S(n-1)+1求解n层塔的移动次数（S(n)为n层塔的移动次数）
   2）在main函数中定义int型变量n并通过scanf()操作得到值作为求Hanoi塔层数的函数参数
   3）定义clock_t类型变量start_time和end_time，调用clock()函数来记录函数开始和结束的执行时间
   4）打印(double)(end_time-start_time)
   5）重复5次实验，取平均值
   6）记录实验数据并绘制图表

四、实验实现过程

1. 求整数平方和问题：
   迭代：
   1） 定义函数sum(int n),利用for循环迭代求解前n项整数平方和
   2） 在main函数中定义int型变量j，通过for循环，以j*100作为参数调用sum函数，让j递增，依次计算前1000、2000、3000，…10000的平方和
   3） 定义clock_t类型变量start_time和end_time，调用clock()函数来记录函数开始和结束的执行时间
   4） 打印(double)(end_time-start_time)
   5） 重复5次实验，取平均值
   6） 记录实验数据并绘制Excel图表

#include<stdio.h>
#include<math.h>
#include<time.h>
#include<stdlib.h>void sum(int n){int res = 0;for(int i=1;i<=n;i++){res = res+i*i;}
}
int main()
{clock_t start_time,end_time;for(int j=1;j<=10;j++){start_time=clock();for(int k=0;k<10000;k++){sum(j*1000);}end_time=clock();printf("%f\n",(double)(end_time-start_time));}return 0;
}

2. 铺地板问题
   1） 定义函数flour(int n),设定n=1与n=2时的基准情形(flour(1)=1,flour(2)=2)，利用递归式flour(n)=flour(n-1)+flour(n-2)求解铺地板的铺法
   2）在main函数中定义int型变量j，通过for循环，以j作为参数调用flour函数，让j递增，依次计算n为30、40、50，…39的铺法
   3）定义clock_t类型变量start_time和end_time，调用clock()函数来记录函数开始和结束的执行时间
   4）打印(double)(end_time-start_time)
   5）重复5次实验，取平均值
   6）记录实验数据并绘制图表

#include<stdio.h>
#include<math.h>
#include<time.h>
#include<stdlib.h>int flour(int n){if((n==1)||(n==2)){return 1;}else{return (flour(n-1)+flour(n-2));}
}
int main()
{clock_t start_time,end_time;for(int j=30;j<40;j++){start_time=clock();flour(j);end_time=clock();printf("%f\n",(double)(end_time-start_time));}return 0;
}

3．Hanoi塔问题：
1）定义函数HanoiTower(int n,char source,char, temp,char target)，设定n=1时为基准情形,利用递归式S(n)=2*S(n-1)+1求解n层塔的移动次数（S(n)为n层塔的移动次数）
2）在main函数中定义int型变量n并通过scanf()操作得到值作为求Hanoi塔层数的函数参数
3）定义clock_t类型变量start_time和end_time，调用clock()函数来记录函数开始和结束的执行时间
4）打印(double)(end_time-start_time)
5）重复5次实验，取平均值
6）记录实验数据并绘制图表

#include<stdio.h>
#include<math.h>
#include<time.h>
#include<stdlib.h>//int i=0;
void HanoiTower(int n,char source,char temp,char target){if(n==1){printf("%c->%c\n",source,target);//i++;}else{HanoiTower(n-1,source,target,temp);printf("%c->%c\n",source,target);//i++;HanoiTower(n-1,temp,source,target);}
}
int main()
{int n;clock_t start_time,end_time;char source='A',temp='B',target='C';scanf("%d",&n);start_time=clock();HanoiTower(n,source,temp,target);end_time=clock();printf("%f",(double)(end_time-start_time));//printf("总移动次数为：%d\n",i);return 0;
}

五、实验结果

1. 求整数平方和问题图表
   
   
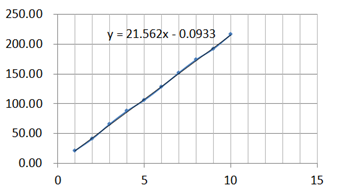
2. 铺地板问题
   
   
   
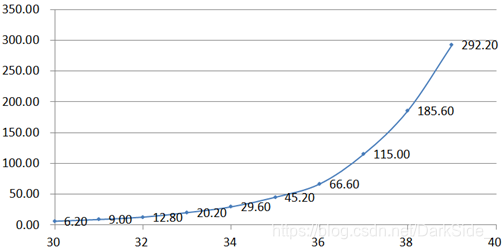
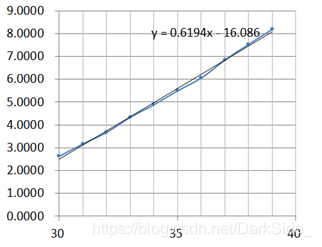
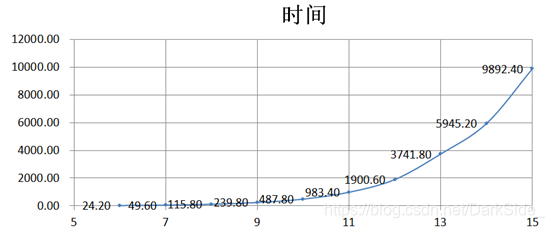
3. Hanoi问题
   
   
   

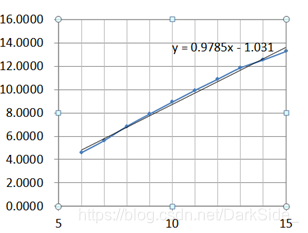
六、实验结论

1. 算法时间复杂度的分析
   对于迭代法求前n个整数的平方和，其时间复杂度T(n)=O(n);对于递归法求铺地板，其时间复杂度T(n)=T(n-1)+T(n-2),T(1)=T(2)=1,T(n)=O(2ⁿ); 对于Hanoi塔问题使用递归，有T(n)=2×T(n-1)+1,T(1)=1,消去系数和常量可得T(n)=O(2ⁿ);

2. 与测量结果进行比对
   求前n个整数的平方和问题得到的结果曲线为一条直线，说明n与时间t成线性关系，与算法的时间复杂度分析所得的T(n)=O(n)吻合；铺地板问题和Hanoi塔问题的结果曲线中，n与log(t)大致成线性关系，与时间复杂度分析吻合。曲线存在误差可能与CPU的内存分配与运行速度有关，n呈指数形式增长，递归占用的内存也迅速增加，大到一定规模时，必将影响运行时间