gmm专题
高斯混合模型(GMM)的EM算法实现
在 聚类算法K-Means, K-Medoids, GMM, Spectral clustering,Ncut一文中我们给出了GMM算法的基本模型与似然函数,在EM算法原理中对EM算法的实现与收敛性证明进行了详细说明。本文主要针对如何用EM算法在混合高斯模型下进行聚类进行代码上的分析说明。 GMM模型: 每个 GMM 由 K 个 Gaussian 分布组成,每个 Gaussian 称为一个“C
GMM与EM算法(一)
EM是我一直想深入学习的算法之一,第一次听说是在NLP课中的HMM那一节,为了解决HMM的参数估计问题,使用了EM算法。在之后的MT中的词对齐中也用到了。在Mitchell的书中也提到EM可以用于贝叶斯网络中。 下面主要介绍EM的整个推导过程。 1. Jensen不等式 回顾优化理论中的一些概念。设f是定义域为实数的函数,如果对于所有的实数x,,那么f是凸函数。当x是向量
前景检测算法_3(GMM)
因为监控发展的需求,目前前景检测的研究还是很多的,也出现了很多新的方法和思路。个人了解的大概概括为以下一些: 帧差、背景减除(GMM、CodeBook、 SOBS、 SACON、 VIBE、 W4、多帧平均……)、光流(稀疏光流、稠密光流)、运动竞争(Motion Competition)、运动模版(运动历史图像)、时间熵……等等。如果加上他们的改进版,那就是很大的一个家族了。
【机器学习】高斯混合模型GMM和EM算法
百度百科:高斯混合模型就是用高斯概率密度函数(正态分布曲线)精确地量化事物,它是一个将事物分解为若干的基于高斯概率密度函数(正态分布曲线)形成的模型。 高斯混合模型(GMM),顾名思义,就是数据可以看作是从数个单高斯分布(GSM)中生成出来的。虽然我们可以用不同的分布来随意地构造 XX Mixture Model ,但是 GMM最为流行。另外,Mixture
【聚类】基于位置(kmeans)层次(agglomerative\birch)基于密度(DBSCAN)基于模型(GMM)
原博文: 一、聚类算法简介 聚类是无监督学习的典型算法,不需要标记结果。试图探索和发现一定的模式,用于发现共同的群体,按照内在相似性将数据划分为多个类别使得内内相似性大,内间相似性小。有时候作为监督学习中稀疏特征的预处理(类似于降维,变成K类后,假设有6类,则每一行都可以表示为类似于000100、010000)。有时候可以作为异常值检测(反欺诈中有用)。 应用场景:新闻聚类、用户购买模式(交
Python数据科学 | Python 离群点检测算法 -- GMM
本文来源公众号“Python数据科学”,仅用于学术分享,侵权删,干货满满。 原文链接:Python 离群点检测算法 -- GMM 星星在天空中聚集或分散,呈现出自然的分布。在统计学中,K-均值法是一种著名的聚类技术,可以识别出不同的聚类。而高斯混合模型(GMM)则提供了另一种视角,假设星星可能遵循多个不同的高斯分布。与 K-均值法相比,GMM 更具灵活性,因为 K-均值法只是 GMM 的一种
聚类算法之GMM聚类算法
上一次我们谈到了用 k-means 进行聚类的方法,这次我们来说一下另一个很流行的算法:Gaussian Mixture Model (GMM)。事实上,GMM 和 k-means 很像,不过 GMM 是学习出一些概率密度函数来(所以 GMM 除了用在 clustering 上之外,还经常被用于 density estimation ),简单地说,k-means 的结果是每个数据点被 as
GMM聚类算法(公式证明分析)
高斯分布 p ( x ∣ μ , σ 2 ) = 1 2 π σ e x p ( − ( x − μ ) 2 2 σ 2 ) p(x|\mu, \sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2}) p(x∣μ,σ2)=2π σ1exp(−2σ2(x−μ)2) d维多元高斯分布 p ( x ∣
KMeans、高斯混合模型(GMM)、分水岭变换、Grabcut等算法基本原理与在图像分割中的应用
KMeans聚类分割: 基本原理 KMeans算法是MacQueen在1967年提出的,是最简单与最常见的数据分类方法之一。它做为一种常见数据分析技术在机器学习、数据挖掘、模式识别、图像分析等领域都有应用。如果从分类角度看,KMeans属于硬分类即需要人为指定分类数目,而MeanSift分类方法则可以根据收敛条件自动决定分类数目。从学习方法上来说,KMeans属于非监督学习方法即整个学习过程中不
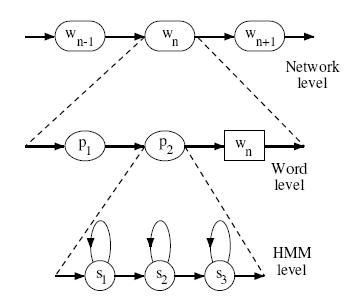
GMM-HMM在语音中的应用常识
本人正在攻读计算机博士学位,目前一直再学习各种模型啊算法之类的。所以一直想把自己的学习过程总结一下,所以就开通了这个博客。 这两天一直再看语音识别方面的知识,想把自己的理解总结一下,希望对其他学习的人有所帮助。 提前需要掌握的知识: 语音信号基础:语音信号的表示形式、分帧、特征(MFCC)、音素等等HMM模型:离散隐马尔科夫模型级3个问题的求解方法GMM:混合高斯模型,用于连续隐马尔科夫模型
【Halcon】Halcon颜色识别之classify_fuses_gmm_based_lut.hdev
* In this example five different color fuses are segmented with* a look-up table classifier (LUT) based on a Gaussian Mixture* Model (GMM).* **把程序窗口、变量窗口、显示窗体变为off状态dev_update_off ()*关闭窗
gmm 背景建模 matlab,GMM混合高斯背景建模C++结合Opencv实现(内附Matlab实现)
最近在做视频流检测方面的工作,一般情况下这种视频流检测是较复杂的场景,比如交通监控,或者各种监控摄像头,场景比较复杂,因此需要构建背景图像,然后去检测场景中每一帧动态变化的前景部分,GMM高斯模型是建模的一种方法,关于高斯建模的介绍有很多博客了,大家可以去找一找,本篇博客主要依赖于上一个老兄,他用matlab实现了GMM模型,我在其基础上利用C++和OpenCV进行了重写,下面会给出C++代码,
GMM/DNN-HMM语音识别:从0讲解HMM类算法原理?看这一篇就够了
摘要 | Abstract 这是一篇对语音识别中的一种热门技术——GMM/DNN-HMM混合系统原理的透彻介绍。 当前网上对HMM类语音识别模型的讲解要么过于简单缺乏深度,要么知识点过于细化零碎分散。而本文旨在为语音识别方面知识储备较少的读者,从头开始深入解读GMM-HMM模型和DNN-HMM模型。 在本文里,我们: 讨论了语音识别里的两个重
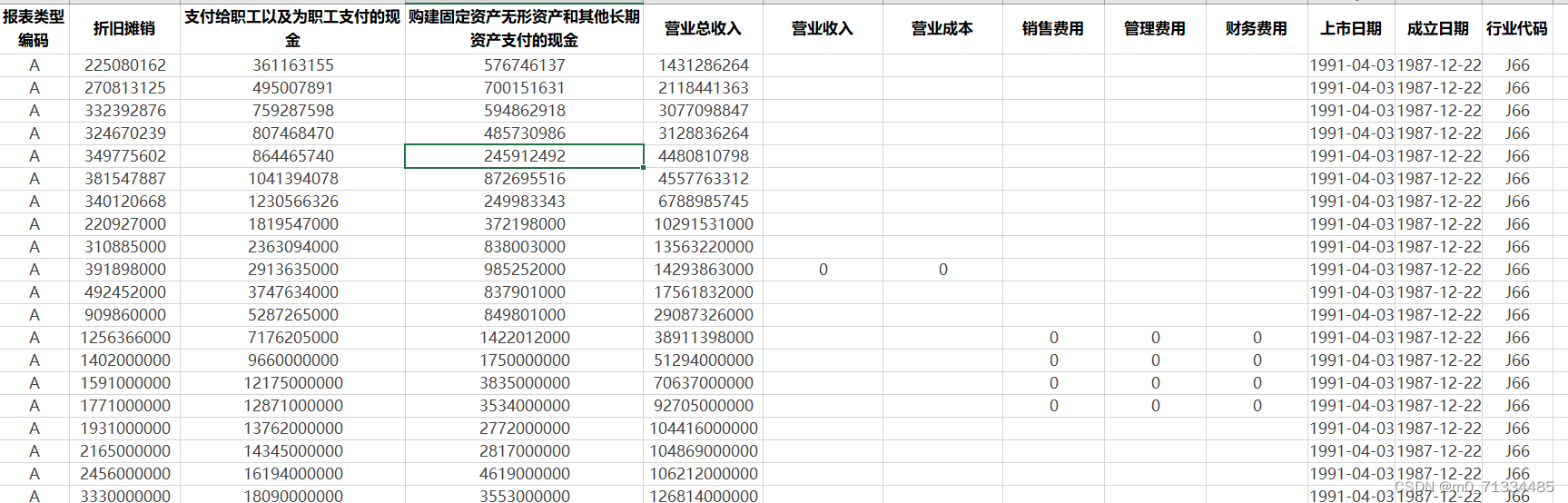
2000-2022年上市公司全要素生产率测算数据合计(原始数据+计算代码+结果)(LP法+OLS法+GMM法+固定效应法)
2000-2022年上市公司全要素生产率测算数据合计(原始数据+计算代码+结果)(LP法+OLS法+GMM法+固定效应法) 1、时间:2000-2022年 2、范围:上市公司 3、指标:证券代码、证券简称、统计截止日期、固定资产净额、year、股票简称、报表类型编码、折旧摊销、支付给职工以及为职工支付的现金、购建固定资产无形资产和其他长期资产支付的现金、营业总收入、营业收入、营业成本、销售费
从EM算法理解k-means与GMM的关系
EM(期望最大化)算法解决的是在概率模型中含有无法观测的隐含变量情况下的参数估计问题,EM算法只保证收敛到局部最优解。EM算法是在最大化目标函数时, 先固定一个变量使整体函数变为凸优化函数, 求导得到最值, 然后利用最优参数更新被固定的变 量, 进入下一个循环。 k-means:E过程,根据固定的各个簇的中心点,对每个样本就近分配所属的簇;M过程,根据样本划分好的簇,重新计算簇的中心点,更新E过
前景检测算法_4(opencv自带GMM)
前面已经有3篇博文介绍了背景减图方面相关知识(见下面的链接),在第3篇博文中自己也实现了gmm简单算法,但效果不是很好,下面来体验下opencv自带2个gmm算法。 opencv实现背景减图法1(codebook和平均背景法) http://www.cnblogs.com/tornadomeet/archive/2012/04/08/2438158.html openc
高斯混合模型(GMM)先验的推断
GMM先验的优化方程 假设图像降质模型为: Y = A X + N Y=AX+N Y=AX+N,我们希望恢复 X X X通过解决一个最大后验问题。 max X P ( X ∣ Y ) = max X P ( Y ∣ X ) P ( X ) = min X − log P ( Y ∣ X ) − log P ( X ) \begin{aligned}\max\limits_
【CV系列】图像算法之九:混合高斯模型GMM
一、 原理 混合高斯背景建模是基于像素样本统计信息的背景表示方法,利用像素在较长时间内大量样本值的概率密度等统计信息(如模式数量、每个模式的均值和标准差)表示背景,然后使用统计差分(如3σ原则)进行目标像素判断,可以对复杂动态背景进行建模,计算量较大。 在混合高斯背景模型中,认为像素之间的颜色信息互不相关,对各像素点的处理都是相互独立的。对于视频图像中的每一个像素点
(二) 三维点云课程---GMM
三维点云课程---GMM 1.前言2.GMM原理2.1E步推导2.2.M步推导2.2.1固定 π k , Σ k \pi_k,\Sigma_k πk,Σk,求解 μ k \mu_k μk2.2.2固定 π k , μ k \pi_k,\mu_k πk,μk,求解 Σ k \Sigma_k Σk2.2.3固定 μ k , Σ k \mu_k,\Sigma_k μk,Σk,求解
机器学习-GMM心得体会
这次又看了两天的GMM,之前看过一次,没看的太明白。这次在前段时间补了一阵子概率论外加昨天学习状态好,把GMM看的明白透彻了。本想用python实现下,却发现,那matlab代码让我看得着实头疼,还得在python和matlab之间寻找各种功能相似的代码,郁闷之下,还是没有完成这个程序。各种数学公式,python中找那些函数,搞的我异常的烦躁。 不浪费时间了,我其实就是想理解清楚这个算法嘛,干嘛
十大机器学习算法(五)——无监督聚类算法 EM 聚类算法(以及GMM)
无监督聚类学习 EM 主要流程:初始化参数 —>> 观察预期结果 —>> 存在误差?重新估计参数 极大似然估计 最大似然估计是假设在总体满足某种分布的情况下 求解满足似然函数(概率密度函数乘积)的最大值的参数 。 目的:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。 原理:“模型已定,参数未知” 情况下,通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本
RBF、GMM、FUZZY
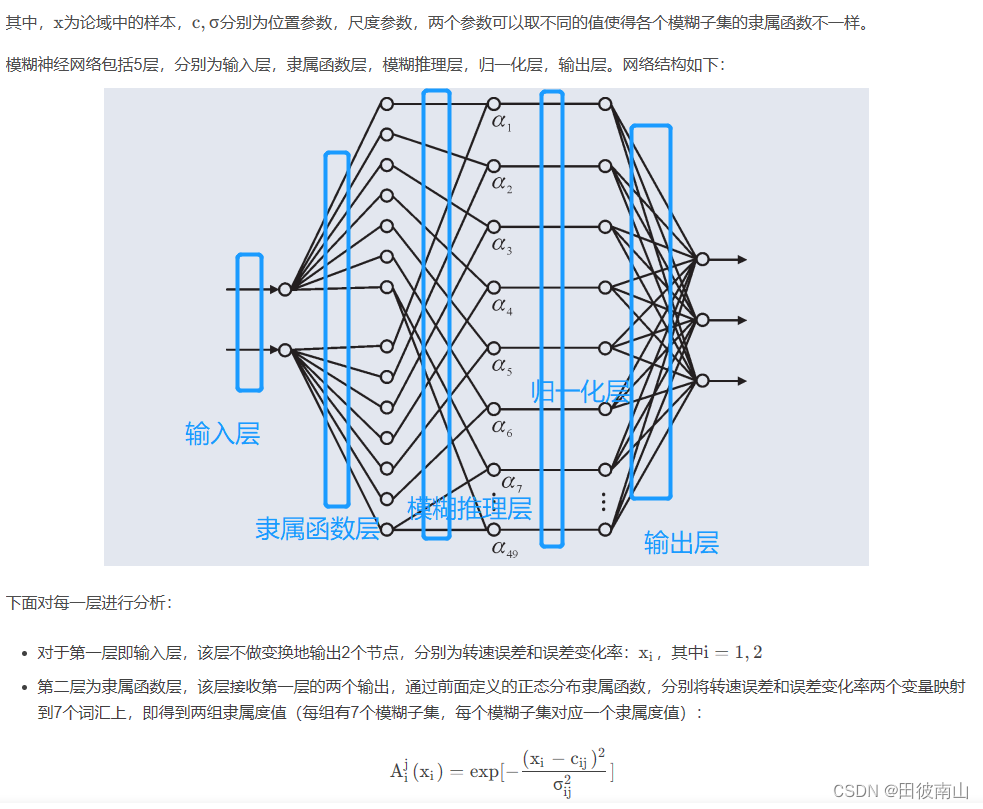
感觉这三种方法有联系,RBF用多个加权高斯拟合值函数,GMM用多个加权高斯拟合联合分布函数,GMM的加权相比于概率更像FUZZY里的隶属度,并且FUZZY的不同规则实现的就是一定程度的聚类。 一、RBF 资料:https://blog.csdn.net/weixin_40802676/article/details/100805545 1、模型描述 总共分为三层,第一层是输入层,第二层隐
HMM+GMM语音识别技术详解级PMTK3中的实例
本人正在攻读计算机博士学位,目前一直再学习各种模型啊算法之类的。所以一直想把自己的学习过程总结一下,所以就开通了这个博客。 这两天一直再看语音识别方面的知识,想把自己的理解总结一下,希望对其他学习的人有所帮助。 提前需要掌握的知识: 语音信号基础:语音信号的表示形式、分帧、特征(MFCC)、音素等等HMM模型:离散隐马尔科夫模型级3个问题的求解方法GMM:混合高斯模
21-高斯混合模型-GMM(Gaussian Mixture Model)
文章目录 1.高斯混合模型GMM的定义1.1高斯混合模型GMM的几何表示1.2高斯混合模型GMM的模型表示2.高斯混合模型的极大似然估计2.1 数据样本的定义 3.高斯混合模型GMM(EM期望最大算法求解)3.1 EM算法(E-Step)3.2 EM算法(E-Step-高斯混合模型代入)3.2 EM算法(M-Step) 1.高斯混合模型GMM的定义 高斯混合模型中的高斯就是指的
EM算法,高斯混合模型(GMM)
目录 1.EM算法 2、高斯混合模型(GMM) 3.GMM和k-means 1.EM算法 具体流程如下: 输入:观测变量数据Y,隐变量数据Z,联合分布P(Y, Z|θ),条件分布P(Z|Y, θ) 输出:模型参数θ 1)选择参数θ的初始值θ(0),开始迭代 2)E步: 记θ(i)次迭代参数为θ的估计值,在第i+1次迭代的E步,计算(基于当前求得的模
gmm中隐变量是什么的_机器学习(十):EM算法与GMM算法原理及案例分析
一、简介 EM算法 最大期望算法(Expectation-maximization algorithm,简称EM,又译期望最大化算法)在统计中被用于寻找依赖于不可观察的隐性变量的概率模型中,参数的最大似然估计。在统计计算中,最大期望(EM)算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。最大期望算法经常用在机器学习和计算机视觉得数据聚类领域。E