本文主要是介绍Python数据科学 | Python 离群点检测算法 -- GMM,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文来源公众号“Python数据科学”,仅用于学术分享,侵权删,干货满满。
原文链接:Python 离群点检测算法 -- GMM
星星在天空中聚集或分散,呈现出自然的分布。在统计学中,K-均值法是一种著名的聚类技术,可以识别出不同的聚类。而高斯混合模型(GMM)则提供了另一种视角,假设星星可能遵循多个不同的高斯分布。与 K-均值法相比,GMM 更具灵活性,因为 K-均值法只是 GMM 的一种特例。
GMM 是由杜达和哈特在 1973 年的论文中提出的无监督学习算法。如今,GMM 已被广泛应用于异常检测、信号处理、语言识别以及音频片段分类等领域。在接下来的章节中,我会首先解释 GMM 及其与 K-均值法的关系,并介绍 GMM 如何定义异常值。然后,我会演示如何使用 GMM 进行建模。
1 什么是高斯混合模型(GMM)
数据点分为四组,分别展示在图 (1) 中。有多种方法可以用来解释这些数据。K-means 方法假设固定数量的聚类,本例中为四个聚类,并将每个数据点分配到其中。而 GMM 方法则假设具有不同均值和标准差的固定数量的高斯分布。
我会将图 (1) 和 (2) 纵向对齐,以比较 GMM 和 K-means。GMM 使用四种分布的概率来描述数据点,而 K-means 将数据点识别到一个聚类中。假设一个数据点位于最左端。K-means 会说它属于聚类 1,而 GMM 可能会说它有 90% 的概率来自红色分布,9% 的概率来自橙色分布,0.9% 的概率来自蓝色分布,0.1% 的概率来自绿色分布,或者 [90%, 9%, 0.9%, 0.1%] 的概率来自 [红色、橙色、蓝色、绿色] 分布。K-means 可以看作是 GMM 的一种特例,因为一个数据点属于一个聚类的概率是 1,而其他所有概率都是 0,或者我们可以说 K-means 进行的是硬分类,而高斯进行的是软分类。

图(1)
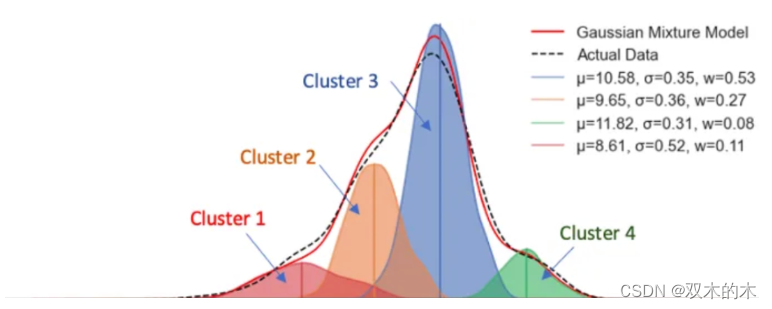
图(2)
2 与 K-means 相比,GMM 有哪些优势?
K-means 是一种简单快速的聚类方法,但可能会强制将数据点归入一个聚类,无法捕捉到数据的模式。相比之下,GMM 能更直观地描述潜在的数据模式,例如对于明天天气的预测,我们会更谨慎地表达预测结果。
3 从高斯到 GMM
GMM的另一个原因是实例的分布是多模态的,即数据分布中存在不止一个"峰值"。多模态分布看起来像单模态分布的混合物。高斯分布是单模态分布,并具有许多良好的特性,因此是混合模型的理想选择。
4 我们试图解决的问题

5 利用贝叶斯定理提供帮助

6 GMM 如何获得参数估计?
三组未知参数需要估计:z、µ、σ。估计标准高斯分布中的µ和σ时,可以使用最大对数似然估计法(MLE)。在线性回归中可能学习过MLE。现在加入一个未知参数z,在应用MLE估算µ和σ之前,可以先猜测z的任意值。然后将θ=(µ, σ)返回计算并更新z。这个迭代过程称为期望最大化算法。
6.1 最大对数似然估计(MLE)

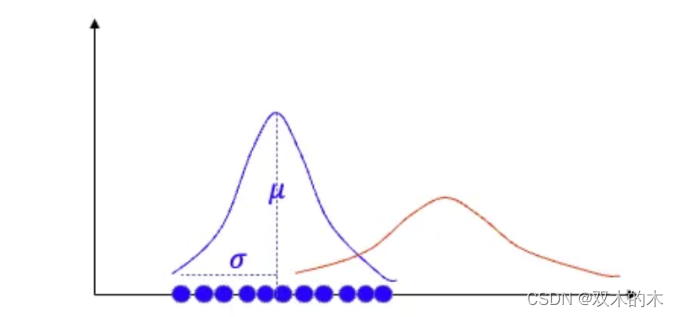
最大对数相似估计
第二个等式表明,由于i.i.d.属性,联合密度概率可以表示为单个密度函数的乘积。i.i.d.属性的假设使得许多优化问题变得容易解决,因为它意味着抽取的样本xi与其他样本无关。在许多应用中,这一假设都不无道理。
最后,我们可以通过分别对(µ, σ)求导并令每个导数为零来求解(µ, σ)的值。
6.2 期望最大化
如果数据点来自多个分布中的不同分布时,估计工作变得更加复杂。但即使如此,我们仍然可以使用期望最大化(E-M)算法来推导参数。该算法利用贝叶斯统计,并包括以下两个步骤(E-M)。

7 GMM 如何定义离群点得分?
GMM输出数据点的概率分布,并以此定义离群值的方法。当拟合值非常低时,数据点被视为离群值。为了保持一致性,低拟合值会被反转为高拟合值,作为离群值分数。
7.1 建模流程
为了离群点分数,需要选择一个阈值,以将离群点分数较高的异常观测值与正常观测值区分开来。如果先验知识表明异常值的百分比不应超过1%,则可以选择一个使异常值约为1%的阈值。
描述性统计(如均值和标准差)对于解释模型的合理性非常重要。如果预期异常组的特征平均值高于正常组,而结果恰恰相反,就需要调查、修改或放弃该特征并重新建模。
7.2 第 1 步 - 建立模型
我将使用 PyOD 的generate_data()函数生成10%的离群值。数据生成过程 (DGP) 将模拟六个变量。尽管模拟数据集有目标变量 Y,但无监督模型只使用 X 变量,而 Y 变量仅用于验证。异常值的百分比被设置为5%,即"contamination=0.05"。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pyod.utils.data import generate_data
contamination = 0.05 # percentage of outliers
n_train = 500 # number of training points
n_test = 500 # number of testing points
n_features = 6 # number of features
X_train, X_test, y_train, y_test = generate_data(n_train=n_train, n_test=n_test, n_features= n_features, contamination=contamination, random_state=123)X_train_pd = pd.DataFrame(X_train)
X_train_pd.head()结果:
把前两个变量绘制成散点图。散点图中的黄色点是百分之十的异常值。紫色点为正常观测值。
# Plot
plt.scatter(X_train_pd[0], X_train_pd[1], c=y_train, alpha=0.8)
plt.title('Scatter plot')
plt.xlabel('x0')
plt.ylabel('x1')
plt.show()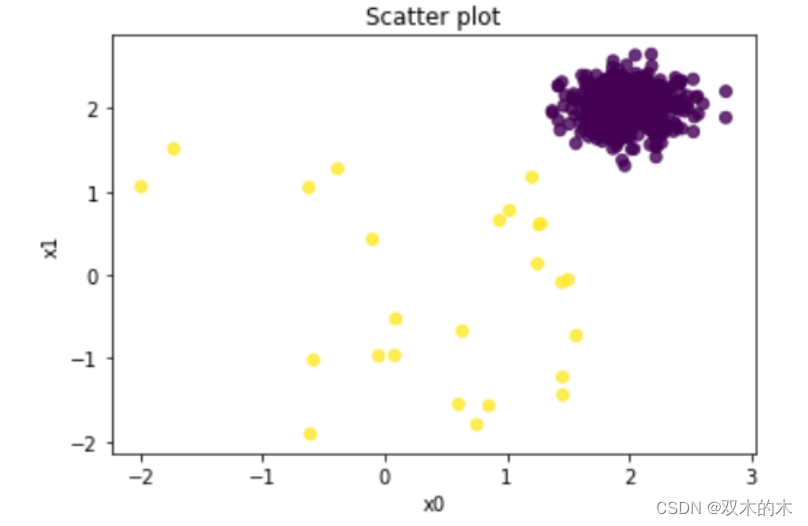
PyOD的统一应用程序接口使建立模型变得非常容易。首先我们声明并拟合模型,然后使用decision_functions()函数生成训练数据和测试数据的离群值。
参数contamination=0.05表示污染率为5%。这个参数代表异常值的百分比。通常情况下,我们无法得知离群值的百分比,因此需要根据先验知识指定一个值。PyOD默认将污染率设为10%。尽管该参数不影响离群值分数的计算,但PyOD会用它来推导离群值的阈值,并应用predict()函数来分配标签(1或0)。我创建了一个简短的函数count_stat()来显示预测值为"1"和"0"的计数。语法.threshold_显示了指定污染率的阈值。任何高于阈值的离群值都被视为离群值。
from pyod.models.gmm import GMM
gmm = GMM(n_components=4, contamination=0.05)
gmm.fit(X_train)# Training data
y_train_scores = gmm.decision_function(X_train)
y_train_pred = gmm.predict(X_train)# Test data
y_test_scores = gmm.decision_function(X_test)
y_test_pred = gmm.predict(X_test) # outlier labels (0 or 1)def count_stat(vector):# Because it is '0' and '1', we can run a count statistic. unique, counts = np.unique(vector, return_counts=True)return dict(zip(unique, counts))print("The training data:", count_stat(y_train_pred))
print("The training data:", count_stat(y_test_pred))
# Threshold for the defined comtanimation rate
print("The threshold for the defined comtanimation rate:" , gmm.threshold_)
The training data: {0: 475, 1: 25}
The training data: {0: 466, 1: 34}
The threshold for the defined comtanimation rate:
4.321327580839012
gmm.get_params()
{'contamination': 0.05,'covariance_type': 'full','init_params': 'kmeans','max_iter': 100,'means_init': None,'n_components': 4,'n_init': 1,'precisions_init': None,'random_state': None,'reg_covar': 1e-06,'tol': 0.001,'warm_start': False,'weights_init': None}
7.3 步骤 2 - 确定合理的阈值
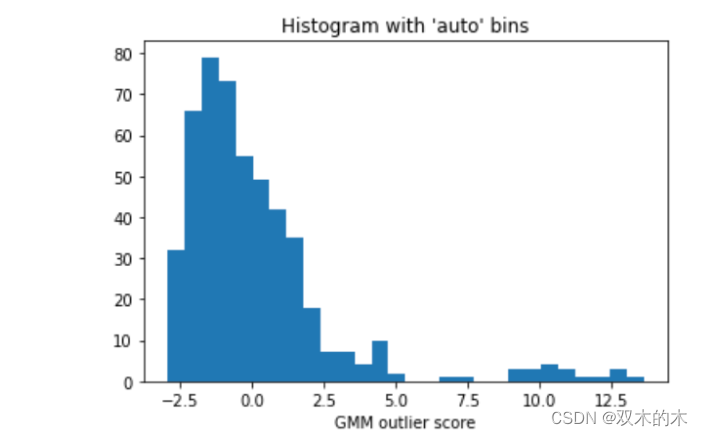
在大多数情况下,我们并不知道异常值的百分比。可以利用离群值的直方图来选择一个合理的阈值,阈值决定异常组的大小。如果先验知识表明异常值的百分比不应超过 1%,可以选择一个导致约 1%异常值的阈值。图 (H.2) 显示了离群值的直方图,我们似乎可以将阈值设置为 200.0,因为直方图中存在一个自然切点。选择较低的阈值会导致较高数量的异常值,反之亦然。
import matplotlib.pyplot as plt
plt.hist(y_train_scores, bins='auto') # arguments are passed to np.histogram
plt.title("Histogram with 'auto' bins")
plt.xlabel('GMM outlier score')
plt.show()
7.4 步骤 3 - 显示正常组和异常组的汇总统计数据
根据第1章所述,两组特征的描述性统计(如均值和标准差)对于证明模型的合理性非常关键。我已经编写了一个简短的函数descriptive_stat_threshold(),用于显示基于阈值的正常组和异常组特征的大小和描述性统计。在接下来的内容中,我将阈值简单设置为5%。您可以测试不同的阈值来确定合理的离群值组大小。
threshold = gmm.threshold_ # Or other value from the above histogramdef descriptive_stat_threshold(df,pred_score, threshold):# Let's see how many '0's and '1's.df = pd.DataFrame(df)df['Anomaly_Score'] = pred_scoredf['Group'] = np.where(df['Anomaly_Score']< threshold, 'Normal', 'Outlier')# Now let's show the summary statistics:cnt = df.groupby('Group')['Anomaly_Score'].count().reset_index().rename(columns={'Anomaly_Score':'Count'})cnt['Count %'] = (cnt['Count'] / cnt['Count'].sum()) * 100 # The count and count %stat = df.groupby('Group').mean().round(2).reset_index() # The avg.stat = cnt.merge(stat, left_on='Group',right_on='Group') # Put the count and the avg. togetherreturn (stat)descriptive_stat_threshold(X_train,y_train_scores, threshold)

上表显示了正常组和异常组的特征。它显示了正常组和异常组的计数和计数百分比。异常分数 "是平均异常分数。提醒您用特征名称标注特征,以便有效展示。该表告诉我们几个重要结果:
-
异常值组的大小: 离群值大约占5%。离群组的大小取决于阈值。如果选择较高的阈值,就会缩小异常值。
-
平均异常值: 异常值组的平均异常值远高于正常组(9.63>-0.37)。不需要对分数做太多解释。
-
各组的特征统计: 离群组的特征均值小于正常组。离群组中特征的均值应该更高还是更低,取决于业务应用。重要的是,所有均值都应与领域知识保持一致。
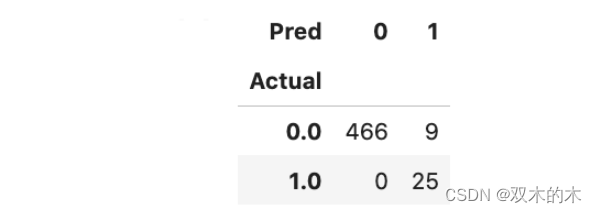
由于我们在数据生成过程中掌握了基本事实,因此可以生成混淆矩阵来了解模型的性能。该模型能够识别所有 25 个离群值。
Actual_pred = pd.DataFrame({'Actual': y_test, 'Anomaly_Score': y_test_scores})
Actual_pred['Pred'] = np.where(Actual_pred['Anomaly_Score']< threshold,0,1)
pd.crosstab(Actual_pred['Actual'],Actual_pred['Pred'])
7.5 通过聚合多个模型实现模型稳定性
分布方法容易受训练数据过拟合和噪声影响。GMM试图学习特定分布的参数,如果分布不准确,会产生异常值。过多的基本高斯分布会导致过度拟合数据。
过度拟合模型会导致不稳定的结果,解决方法是使用一系列超参数训练模型,然后汇总得分,以降低过拟合的几率,并提高预测准确率。
为避免假设大量混合成分,创建了七个不同聚类的GMM模型,并汇总平均预测值作为最终模型预测值。
from pyod.models.combination import aom, moa, average, maximization
from pyod.utils.utility import standardizer
from pyod.models.gmm import GMM# Standardize data
X_train_norm, X_test_norm = standardizer(X_train, X_test)
# Test a range of clusters from 2 to 8. There will be 7 models.
n_clf = 7
k_list = [2, 3, 4, 5, 6, 7, 8]
# Just prepare data frames so we can store the model results
train_scores = np.zeros([X_train.shape[0], n_clf])
test_scores = np.zeros([X_test.shape[0], n_clf])
train_scores.shape
# Modeling
for i in range(n_clf):k = k_list[i]gmm = GMM(n_components = k) gmm.fit(X_train_norm)# Store the results in each column:test_scores[:, i] = gmm.decision_function(X_test_norm)
# Decision scores have to be normalized before combination
train_scores_norm, test_scores_norm = standardizer(train_scores,test_scores)
预测结果被归一化并存储在数据帧 "train_scores_norm "中。PyOD 模块提供了四种聚合方法,您只需使用一种方法即可得出结果。
# Combination by average
# The test_scores_norm is 500 x 7. The "average" function will take the average of the 7 columns.
# The result "y_by_average" is a single column:
y_train_by_average = average(train_scores_norm)
y_test_by_average = average(test_scores_norm)
import matplotlib.pyplot as plt
plt.hist(y_train_by_average, bins='auto') # arguments are passed to np.histogram
plt.title("Combination by average")
plt.show()
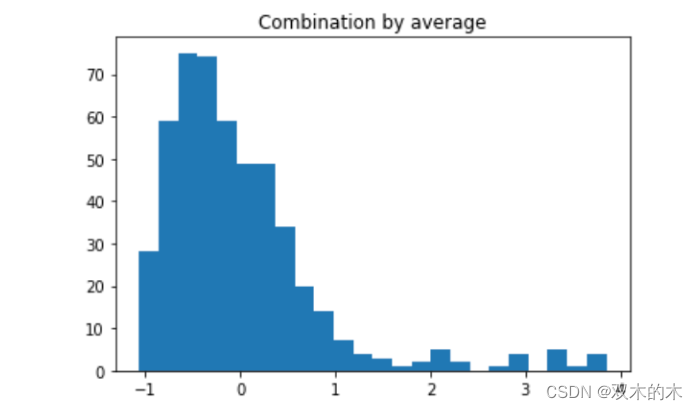
训练数据平均预测值直方图
上图描绘了离群值的直方图,建议将 2.0 作为阈值。接着,表中的描述性统计表,确定了 22 个数据点为离群值。
descriptive_stat_threshold(X_train,y_train_by_average, 2.0)

image
8 GMM 算法概述
-
GMM使用不同分布的概率来描述数据点,而K-means将数据点识别到一个聚类中。
-
条件概率p(z|x)可理解为"给定数据点x,它属于z的概率为p(z|x)",利用贝叶斯定理可得后验概率p(z|x)。
-
GMM使用期望最大化法找出后验概率p(z|x)的最佳值。E步为数据点属于某一分布的概率指定一个初始"猜测",然后计算出MLE。M步是估计参数的标准MLE。新参数输入E步,再次分配后验概率。E步和M步将反复进行,直到收敛。
-
与基本高斯分布拟合值较低的数据点被视为异常值。
THE END !
文章结束,感谢阅读。您的点赞,收藏,评论是我继续更新的动力。大家有推荐的公众号可以评论区留言,共同学习,一起进步。
这篇关于Python数据科学 | Python 离群点检测算法 -- GMM的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!