本文主要是介绍21-高斯混合模型-GMM(Gaussian Mixture Model),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1.高斯混合模型GMM的定义
- 1.1高斯混合模型GMM的几何表示
- 1.2高斯混合模型GMM的模型表示
- 2.高斯混合模型的极大似然估计
- 2.1 数据样本的定义
- 3.高斯混合模型GMM(EM期望最大算法求解)
- 3.1 EM算法(E-Step)
- 3.2 EM算法(E-Step-高斯混合模型代入)
- 3.2 EM算法(M-Step)
1.高斯混合模型GMM的定义
高斯混合模型中的高斯就是指的是高斯分布,顾名思义,就是多个高斯分布组成的混合模型。由中心极限定理可得,把数据看作成高斯分布是比较合理的做法。高斯混合模型的产生是因为数据在非常复杂的情况下,我们无法通过单个高斯模型进行拟合,只能够通过通过多个高斯进行不同权重的拟合才行。这样就产生了高斯混合模型
1.1高斯混合模型GMM的几何表示

从几何角度来看是比较简单的,当数据由高斯分布N1和高斯分布N2组成的,那么高斯分布N3可以看作是两个高斯分布加权平均来组成的。
P ( x ) = ∑ k = 1 K α k N ( μ k , Σ k ) , ∑ k = 1 K α k = 1 (1) P(x)=\sum_{k=1}^K\alpha_kN(\mu_k,\Sigma_k),\sum_{k=1}^K\alpha_k=1\tag1 P(x)=k=1∑KαkN(μk,Σk),k=1∑Kαk=1(1)
- α k : 表 示 每 个 高 斯 分 布 在 整 个 高 斯 分 布 的 权 重 \alpha_k:表示每个高斯分布在整个高斯分布的权重 αk:表示每个高斯分布在整个高斯分布的权重
1.2高斯混合模型GMM的模型表示
我们知道当数据两维以上时,那么数据的概率密度函数就是一个高斯曲面,无法用曲线表示,所以我们只能用等高线来表示相关数据。那么对于下图来说,样本 X k X_k Xk既属于N1,也属于N2,只是我们看起来属于N1的概率更大。

我们定义样本数据如下:
-
X:observed data 观测数据;
-
Z:latent data 隐变量数据;表示对应的样本X是属于哪一个高斯分布的;
我们引入的Z是为了表示数据X属于哪一个分布,所以可知Z是离散型随机变量。且假设Z满足如下分布:
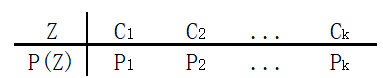
-
∑ k = 1 K P k = 1 \sum_{k=1}^KP_k=1 ∑k=1KPk=1
那么对于样本数据X来说,我们可以引入一个变量Z,那么数据生成可以用两步来表示: -
用Z分布来表示该样本属于哪一个高斯分布 C k C_k Ck
-
当选定了第 C k C_k Ck高斯分布后,再在高斯分布中采样数据X;
具体形象描述为:
假设我们有一个骰子,这个骰子的K个面被不同比例的油漆涂上,我们随机投掷骰子,那么我们就有K个高斯分布,我们每次投一个骰子时,就会出现第K个面,然后我们在第K个面中采样数据X。这样就可以通过两个步骤来进行合成数据X;这个过程重复N次就是高斯混合模型的生成方式。 -
概率图:

-
参数P用实心点表示
2.高斯混合模型的极大似然估计
2.1 数据样本的定义
为了方便后续的表示,我们定义如下参数:
- X:observed data 观测数据 X = ( x 1 , x 2 , . . . , x N ) X=(x_1,x_2,...,x_N) X=(x1,x2,...,xN)
- Z:latent data 隐变量 Z = ( z 1 , z 2 , . . . , z N ) Z=(z_1,z_2,...,z_N) Z=(z1,z2,...,zN)
- (X,Z):complete data 完整数据 ( X , Z ) = { ( x 1 , z 1 ) , ( x 2 , z 2 ) , . . . , ( x N , z N ) , } (X,Z)=\{(x_1,z_1),(x_2,z_2),...,(x_N,z_N),\} (X,Z)={(x1,z1),(x2,z2),...,(xN,zN),}
- θ : p a r a m e t e r 参 数 : θ = { P 1 , P 2 , . . . , P k , μ 1 , μ 2 , . . . , μ k , Σ 1 , Σ 2 , . . . , Σ k } \theta:parameter 参数:\theta=\{P_1,P_2,...,P_k,\mu_1,\mu_2,...,\mu_k,\Sigma_1,\Sigma_2,...,\Sigma_k\} θ:parameter参数:θ={P1,P2,...,Pk,μ1,μ2,...,μk,Σ1,Σ2,...,Σk}
对于已知数据X,为了搞清楚高斯混合模型的相关参数,我们首先想到的是极大似然估计法MLE。我们的目标是为了找到一组参数 θ \theta θ,使得参数 θ \theta θ能够让 log P ( X ∣ θ ) \log P(X|\theta) logP(X∣θ)取得最大值;
θ ^ = arg max θ log P ( X ∣ θ ) (2) \hat{\theta}=\mathop{\arg\max}\limits_{\theta}\log P(X|\theta) \tag 2 θ^=θargmaxlogP(X∣θ)(2)
由边缘概率P(X)和联合概率P(X,Z)的关系可得:
P ( X ) = ∑ Z P ( X , Z ) = ∑ k = 1 K P ( X , Z = C k ) = ∑ k = 1 K P ( Z = C k ) ⋅ P ( X ∣ Z = C k ) (3) P(X)=\sum_{Z}P(X,Z)=\sum_{k=1}^{K}P(X,Z=C_k)=\sum_{k=1}^{K}P(Z=C_k)·P(X|Z=C_k)\tag 3 P(X)=Z∑P(X,Z)=k=1∑KP(X,Z=Ck)=k=1∑KP(Z=Ck)⋅P(X∣Z=Ck)(3)
- Z 是 满 足 离 散 概 率 分 布 , 即 : P ( Z = C k ) = P k Z是满足离散概率分布,即:P(Z=C_k)=P_k Z是满足离散概率分布,即:P(Z=Ck)=Pk
- P ( X ∣ Z = C k ) 满 足 高 斯 分 布 , 即 : P ( X ∣ Z = C k ) = N ( x i ∣ μ k , Σ k ) P(X|Z=C_k)满足高斯分布,即:P(X|Z=C_k)=N(x_i|\mu_k,\Sigma_k) P(X∣Z=Ck)满足高斯分布,即:P(X∣Z=Ck)=N(xi∣μk,Σk)
P ( X ) = ∑ k = 1 K P k ⋅ N ( x i ∣ μ k , Σ k ) (4) P(X)=\sum_{k=1}^{K}P_k·N(x_i|\mu_k,\Sigma_k)\tag 4 P(X)=k=1∑KPk⋅N(xi∣μk,Σk)(4)
所以目标函数可以表示如下:
θ ^ M L E = arg max θ log P ( X ∣ θ ) = arg max θ log ∏ i = 1 N P ( x i ∣ θ ) = arg max θ ∑ i = 1 N log P ( x i ∣ θ ) (5) \hat{\theta}_{MLE}=\mathop{\arg\max}\limits_{\theta}\log P(X|\theta)=\mathop{\arg\max}\limits_{\theta}\log \prod_{i=1}^{N}P(x_i|\theta)=\mathop{\arg\max}\limits_{\theta} \sum_{i=1}^{N}\log P(x_i|\theta)\tag 5 θ^MLE=θargmaxlogP(X∣θ)=θargmaxlogi=1∏NP(xi∣θ)=θargmaxi=1∑NlogP(xi∣θ)(5)
θ ^ M L E = arg max θ ∑ i = 1 N log [ ∑ k = 1 K P k ⋅ N ( x i ∣ μ k , Σ k ) ] (6) \hat{\theta}_{MLE}=\mathop{\arg\max}\limits_{\theta} \sum_{i=1}^{N}\log [\sum_{k=1}^{K}P_k·N(x_i|\mu_k,\Sigma_k)]\tag 6 θ^MLE=θargmaxi=1∑Nlog[k=1∑KPk⋅N(xi∣μk,Σk)](6) - θ : p a r a m e t e r 参 数 : θ = { P 1 , P 2 , . . . , P k , μ 1 , μ 2 , . . . , μ k , Σ 1 , Σ 2 , . . . , Σ k } \theta:parameter 参数:\theta=\{P_1,P_2,...,P_k,\mu_1,\mu_2,...,\mu_k,\Sigma_1,\Sigma_2,...,\Sigma_k\} θ:parameter参数:θ={P1,P2,...,Pk,μ1,μ2,...,μk,Σ1,Σ2,...,Σk}
之前我们在求高斯分布的极大似然估计的时候,因为单个的高斯分布概率密度函数是:
log P ( x i ∣ θ ) = log [ 1 2 π σ ⋅ e x p ( − ( x − μ ) 2 2 σ 2 ) ] (7) \log P(x_i|\theta)=\log [\frac{1}{\sqrt{2\pi}\sigma}·exp^{(-\frac{(x-\mu)^2}{2\sigma^2})} ]\tag 7 logP(xi∣θ)=log[2πσ1⋅exp(−2σ2(x−μ)2)](7)
由上式可以看出,当我们使用对数函数时,因为单个高斯分布里面是一个乘积的形式,那么我们取对数后可以变成两个式子的和,所以可以把上述公式进行分割求导,简化运算。但是对于高斯混合模型来说公式<6>,发现属于如下求和形式:
θ ^ M L E = arg max θ ∑ i = 1 N log [ △ 1 + △ 2 , . . . , △ N ] (8) \hat{\theta}_{MLE}=\mathop{\arg\max}\limits_{\theta} \sum_{i=1}^{N}\log [\triangle_1+\triangle_2,...,\triangle_N]\tag 8 θ^MLE=θargmaxi=1∑Nlog[△1+△2,...,△N](8)
那么就无法进行分割上述公式,所以我们直接对高斯混合模型来说,直接用极大似然估计是行不通的,没法进行下去了。为了解决这个问题,我们引入之前的EM期望最大算法来求解高斯混合模型GMM。EM算法的目的不就是为了求期望最大嘛,所以这里用EM算法就情理之中了。
3.高斯混合模型GMM(EM期望最大算法求解)
3.1 EM算法(E-Step)
我们发现用极大似然估计法无法求得数据X的参数 θ \theta θ,所以我们用之前讲解的EM期望最大算法进行迭代求解参数 θ \theta θ:
EM算法公式如下:
θ ( t + 1 ) = arg max θ E Z ∼ { Z ∣ X , θ ( t ) } log P ( X , Z ∣ θ ) (9) \theta^{(t+1)}=\mathop{\arg\max}\limits_{\theta}\mathbb{E}_{Z\sim \{Z|X,\theta^{(t)}\}}\log P(X,Z|\theta)\tag{9} θ(t+1)=θargmaxEZ∼{Z∣X,θ(t)}logP(X,Z∣θ)(9)
- 我 们 定 义 : Q ( θ , θ ( t ) ) = E Z ∼ { Z ∣ X , θ ( t ) } log P ( X , Z ∣ θ ) 我们定义:Q(\theta,\theta^{(t)})=\mathbb{E}_{Z\sim \{Z|X,\theta^{(t)}\}}\log P(X,Z|\theta) 我们定义:Q(θ,θ(t))=EZ∼{Z∣X,θ(t)}logP(X,Z∣θ)
首先我们对 Q ( θ , θ ( t ) ) Q(\theta,\theta^{(t)}) Q(θ,θ(t))进行展开表达:
Q ( θ , θ ( t ) ) = E Z ∼ { Z ∣ X , θ ( t ) } log P ( X , Z ∣ θ ) Q(\theta,\theta^{(t)})=\mathbb{E}_{Z\sim \{Z|X,\theta^{(t)}\}}\log P(X,Z|\theta) Q(θ,θ(t))=EZ∼{Z∣X,θ(t)}logP(X,Z∣θ)
将期望转换成积分形式可得:
= ∫ Z log P ( X , Z ∣ θ ) ⋅ P ( Z ∣ X , θ ( t ) ) d Z \quad=\int_Z \log P(X,Z|\theta)·P(Z|X,\theta^{(t)})dZ =∫ZlogP(X,Z∣θ)⋅P(Z∣X,θ(t))dZ
由于数据X之间是独立同分布的,所以可变成如下:
= ∫ Z log ∏ i = 1 N P ( x i , z i ∣ θ ) ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) d Z \quad=\int_Z \log \prod_{i=1}^{N}P(x_i,z_i|\theta)·\prod_{i=1}^{N} P(z_i|x_i,\theta^{(t)})dZ =∫Zlog∏i=1NP(xi,zi∣θ)⋅∏i=1NP(zi∣xi,θ(t))dZ
展开后可得:
= ∫ Z [ log P ( x 1 , z 1 ∣ θ ) + . . + log P ( x i , z i ∣ θ ) ] ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) d Z \quad=\int_Z [ \log P(x_1,z_1|\theta)+..+\log P(x_i,z_i|\theta)]·\prod_{i=1}^{N}P(z_i|x_i,\theta^{(t)})dZ =∫Z[logP(x1,z1∣θ)+..+logP(xi,zi∣θ)]⋅∏i=1NP(zi∣xi,θ(t))dZ
为了简化上述公式,我们首先对其中一项式子进行简化:
∫ Z [ log P ( x 1 , z 1 ∣ θ ) ] ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) d Z \quad\int_Z [ \log P(x_1,z_1|\theta)]·\prod_{i=1}^{N}P(z_i|x_i,\theta^{(t)})dZ ∫Z[logP(x1,z1∣θ)]⋅∏i=1NP(zi∣xi,θ(t))dZ
将Z分解成 Z 1 , Z 2 , . . . , Z N Z_1,Z_2,...,Z_N Z1,Z2,...,ZN
∫ Z 1 , Z 2 , . . . , Z N [ log P ( x 1 , z 1 ∣ θ ) ] ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) d Z \quad\int_{Z_1,Z_2,...,Z_N} [ \log P(x_1,z_1|\theta)]·\prod_{i=1}^{N}P(z_i|x_i,\theta^{(t)})dZ ∫Z1,Z2,...,ZN[logP(x1,z1∣θ)]⋅∏i=1NP(zi∣xi,θ(t))dZ
= ∫ Z 1 [ log P ( x 1 , z 1 ∣ θ ) ] ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) d Z 1 ⋅ ∫ Z 2 P ( z 2 ∣ x 2 , θ ( t ) ) d Z 2 ⏟ = 1 ⋅ . . . ∫ Z N P ( z N ∣ x N , θ ( t ) ) d Z N ⏟ = 1 \quad=\int_{Z_1} [ \log P(x_1,z_1|\theta)]·P(z_1|x_1,\theta^{(t)})dZ_1·\underbrace{\int_{Z_2}P(z_2|x_2,\theta^{(t)}) dZ_2}_{=1}·...\underbrace{\int_{Z_N}P(z_N|x_N,\theta^{(t)}) dZ_N}_{=1} =∫Z1[logP(x1,z1∣θ)]⋅P(z1∣x1,θ(t))dZ1⋅=1 ∫Z2P(z2∣x2,θ(t))dZ2⋅...=1 ∫ZNP(zN∣xN,θ(t))dZN
= ∫ Z 1 [ log P ( x 1 , z 1 ∣ θ ) ] ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) d Z 1 \quad=\int_{Z_1} [ \log P(x_1,z_1|\theta)]·P(z_1|x_1,\theta^{(t)})dZ_1 =∫Z1[logP(x1,z1∣θ)]⋅P(z1∣x1,θ(t))dZ1
因为Z为离散型变量,故积分可转换成如下:
= ∑ Z 1 [ log P ( x 1 , z 1 ∣ θ ) ] ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) \quad=\sum_{Z_1} [ \log P(x_1,z_1|\theta)]·P(z_1|x_1,\theta^{(t)}) =∑Z1[logP(x1,z1∣θ)]⋅P(z1∣x1,θ(t))
所以:
Q ( θ , θ ( t ) ) = ∑ Z 1 [ log P ( x 1 , z 1 ∣ θ ) ] ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) + . . . + ∑ Z N [ log P ( x N , z N ∣ θ ) ] ⋅ P ( z N ∣ x N , θ ( t ) ) Q(\theta,\theta^{(t)})=\sum_{Z_1} [ \log P(x_1,z_1|\theta)]·P(z_1|x_1,\theta^{(t)})+...+\sum_{Z_N} [ \log P(x_N,z_N|\theta)]·P(z_N|x_N,\theta^{(t)}) Q(θ,θ(t))=∑Z1[logP(x1,z1∣θ)]⋅P(z1∣x1,θ(t))+...+∑ZN[logP(xN,zN∣θ)]⋅P(zN∣xN,θ(t))
整理上式公式可得:
Q ( θ , θ ( t ) ) = ∑ i = 1 N ∑ Z i [ log P ( x i , z i ∣ θ ) ] ⋅ P ( z i ∣ x i , θ ( t ) ) (10) Q(\theta,\theta^{(t)})=\sum_{i=1}^{N}\sum_{Z_i} [ \log P(x_i,z_i|\theta)]·P(z_i|x_i,\theta^{(t)})\tag{10} Q(θ,θ(t))=i=1∑NZi∑[logP(xi,zi∣θ)]⋅P(zi∣xi,θ(t))(10)
那么我们接下来的步骤是将高斯混合模型嵌入到上式EM算法中。即将上述公式的 log P ( x i , z i ∣ θ ) 和 P ( z i ∣ x i , θ ( t ) ) \log P(x_i,z_i|\theta)和P(z_i|x_i,\theta^{(t)}) logP(xi,zi∣θ)和P(zi∣xi,θ(t))用高斯混合模型的相关概率进行表示即可
3.2 EM算法(E-Step-高斯混合模型代入)
对于高斯混合模型来说:我们定义如下参数:
- X:observed data 观测数据 X = ( x 1 , x 2 , . . . , x N ) X=(x_1,x_2,...,x_N) X=(x1,x2,...,xN)
- Z:latent data 隐变量 Z = ( z 1 , z 2 , . . . , z N ) Z=(z_1,z_2,...,z_N) Z=(z1,z2,...,zN)
- (X,Z):complete data 完整数据 ( X , Z ) = { ( x 1 , z 1 ) , ( x 2 , z 2 ) , . . . , ( x N , z N ) , } (X,Z)=\{(x_1,z_1),(x_2,z_2),...,(x_N,z_N),\} (X,Z)={(x1,z1),(x2,z2),...,(xN,zN),}
- θ : p a r a m e t e r 参 数 : θ = { P 1 , P 2 , . . . , P k , μ 1 , μ 2 , . . . , μ k , Σ 1 , Σ 2 , . . . , Σ k } \theta:parameter 参数:\theta=\{P_1,P_2,...,P_k,\mu_1,\mu_2,...,\mu_k,\Sigma_1,\Sigma_2,...,\Sigma_k\} θ:parameter参数:θ={P1,P2,...,Pk,μ1,μ2,...,μk,Σ1,Σ2,...,Σk}
我们在上面已经得出如下结论:
P ( X ) = ∑ k = 1 K P k ⋅ N ( x i ∣ μ k , Σ k ) (11) P(X)=\sum_{k=1}^{K}P_k·N(x_i|\mu_k,\Sigma_k)\tag {11} P(X)=k=1∑KPk⋅N(xi∣μk,Σk)(11)
又由于贝叶斯公式 { P ( X , Z ) = P ( Z ) ⋅ P ( X ∣ Z ) } \{P(X,Z)=P(Z)·P(X|Z)\} {P(X,Z)=P(Z)⋅P(X∣Z)},且: P ( Z ) = P z ; P ( X ∣ Z ) = N ( X ∣ μ z , Σ k ) P(Z)=P_z;P(X|Z)=N(X|\mu_z,\Sigma_k) P(Z)=Pz;P(X∣Z)=N(X∣μz,Σk)故:
P ( X , Z ) = P Z ⋅ N ( X ∣ μ z , Σ k ) (12) P(X,Z)=P_Z·N(X|\mu_z,\Sigma_k)\tag {12} P(X,Z)=PZ⋅N(X∣μz,Σk)(12)
因 为 贝 叶 斯 公 式 可 得 : P ( Z ∣ X ) = P ( X , Z ) / P ( X ) , 代 入 上 式 可 得 : 因为贝叶斯公式可得: P(Z|X)=P(X,Z)/P(X),代入上式可得: 因为贝叶斯公式可得:P(Z∣X)=P(X,Z)/P(X),代入上式可得:
P ( Z ∣ X , θ ( t ) ) = P ( X , Z , θ ( t ) ) P ( X , θ ( t ) ) = ⋅ P Z i θ ( t ) ⋅ N ( x i ∣ μ Z i θ ( t ) , Σ Z i θ ( t ) ) ∑ k = 1 K P k θ ( t ) ⋅ N ( x i ∣ μ k θ ( t ) , Σ k θ ( t ) ) (13) P(Z|X,\theta^{(t)})=\frac{P(X,Z,\theta^{(t)})}{P(X,\theta^{(t)})}=·\frac{P_{Z_i}^{\theta^{(t)}}·N(x_i|\mu_{Z_i}^{\theta^{(t)}},\Sigma_{Z_i}^{\theta^{(t)}})}{\sum_{k=1}^{K}P_k^{\theta^{(t)}}·N(x_i|\mu_k^{\theta^{(t)}},\Sigma_k^{\theta^{(t)}})}\tag {13} P(Z∣X,θ(t))=P(X,θ(t))P(X,Z,θ(t))=⋅∑k=1KPkθ(t)⋅N(xi∣μkθ(t),Σkθ(t))PZiθ(t)⋅N(xi∣μZiθ(t),ΣZiθ(t))(13)
将此时算出来的 P ( Z ∣ X ) 和 P ( X , Z ) 代 入 到 之 前 公 式 Q ( θ , θ ( t ) ) 中 可 得 : P(Z|X)和P(X,Z)代入到之前公式Q(\theta,\theta^{(t)})中可得: P(Z∣X)和P(X,Z)代入到之前公式Q(θ,θ(t))中可得:
Q ( θ , θ ( t ) ) = ∑ i = 1 N ∑ Z i log [ P Z i ⋅ N ( x i ∣ μ z , Σ k ) ] ⋅ P Z i θ ( t ) ⋅ N ( x i ∣ μ Z i θ ( t ) , Σ Z i θ ( t ) ) ∑ k = 1 K P k θ ( t ) ⋅ N ( x i ∣ μ k θ ( t ) , Σ k θ ( t ) ) (14) Q(\theta,\theta^{(t)})=\sum_{i=1}^{N}\sum_{Z_i} \log [P_{Z_i}·N(x_i|\mu_z,\Sigma_k)]·\frac{P_{Z_i}^{\theta^{(t)}}·N(x_i|\mu_{Z_i}^{\theta^{(t)}},\Sigma_{Z_i}^{\theta^{(t)}})}{\sum_{k=1}^{K}P_k^{\theta^{(t)}}·N(x_i|\mu_k^{\theta^{(t)}},\Sigma_k^{\theta^{(t)}})}\tag{14} Q(θ,θ(t))=i=1∑NZi∑log[PZi⋅N(xi∣μz,Σk)]⋅∑k=1KPkθ(t)⋅N(xi∣μkθ(t),Σkθ(t))PZiθ(t)⋅N(xi∣μZiθ(t),ΣZiθ(t))(14)
3.2 EM算法(M-Step)
我们已经求得了EM算法中的E-Step 得到 Q ( θ , θ ( t ) ) Q(\theta,\theta^{(t)}) Q(θ,θ(t)),现在只要求最大值即可:
θ ( t + 1 ) = arg max θ E Z ∼ { Z ∣ X , θ ( t ) } log P ( X , Z ∣ θ ) = arg max θ Q ( θ , θ ( t ) ) (15) \theta^{(t+1)}=\mathop{\arg\max}\limits_{\theta}\mathbb{E}_{Z\sim \{Z|X,\theta^{(t)}\}}\log P(X,Z|\theta)=\mathop{\arg\max}\limits_{\theta}Q(\theta,\theta^{(t)})\tag{15} θ(t+1)=θargmaxEZ∼{Z∣X,θ(t)}logP(X,Z∣θ)=θargmaxQ(θ,θ(t))(15)
整理上式可得:
θ ( t + 1 ) = arg max θ ∑ i = 1 N ∑ Z i log [ P Z i ⋅ N ( x i ∣ μ z , Σ k ) ] ⋅ P Z i θ ( t ) ⋅ N ( x i ∣ μ Z i θ ( t ) , Σ Z i θ ( t ) ) ∑ k = 1 K P k θ ( t ) ⋅ N ( x i ∣ μ k θ ( t ) , Σ k θ ( t ) ) ⏟ P ( Z i ∣ X i , θ ( t ) ) (16) \theta^{(t+1)}=\mathop{\arg\max}\limits_{\theta}\sum_{i=1}^{N}\sum_{Z_i} \log [P_{Z_i}·N(x_i|\mu_z,\Sigma_k)]·\underbrace{\frac{P_{Z_i}^{\theta^{(t)}}·N(x_i|\mu_{Z_i}^{\theta^{(t)}},\Sigma_{Z_i}^{\theta^{(t)}})}{\sum_{k=1}^{K}P_k^{\theta^{(t)}}·N(x_i|\mu_k^{\theta^{(t)}},\Sigma_k^{\theta^{(t)}})}}_{P(Z_i|X_i,\theta^{(t)})}\tag{16} θ(t+1)=θargmaxi=1∑NZi∑log[PZi⋅N(xi∣μz,Σk)]⋅P(Zi∣Xi,θ(t)) ∑k=1KPkθ(t)⋅N(xi∣μkθ(t),Σkθ(t))PZiθ(t)⋅N(xi∣μZiθ(t),ΣZiθ(t))(16)
θ ( t + 1 ) = arg max θ ∑ i = 1 N ∑ Z i log [ P Z i ⋅ N ( x i ∣ μ z , Σ k ) ] ⋅ P ( Z i ∣ X i , θ ( t ) ) (17) \theta^{(t+1)}=\mathop{\arg\max}\limits_{\theta}\sum_{i=1}^{N}\sum_{Z_i} \log [P_{Z_i}·N(x_i|\mu_z,\Sigma_k)]·{P(Z_i|X_i,\theta^{(t)})}\tag{17} θ(t+1)=θargmaxi=1∑NZi∑log[PZi⋅N(xi∣μz,Σk)]⋅P(Zi∣Xi,θ(t))(17)
求和符号交换位置
= arg max θ ∑ Z i ∑ i = 1 N log [ P Z i ⋅ N ( x i ∣ μ z , Σ k ) ] ⋅ P ( Z i ∣ X i , θ ( t ) ) (18) =\mathop{\arg\max}\limits_{\theta}\sum_{Z_i}\sum_{i=1}^{N} \log [P_{Z_i}·N(x_i|\mu_z,\Sigma_k)]·{P(Z_i|X_i,\theta^{(t)})} \tag{18} =θargmaxZi∑i=1∑Nlog[PZi⋅N(xi∣μz,Σk)]⋅P(Zi∣Xi,θ(t))(18)
将 ∑ Z i 分 解 \sum_{Z_i}分解 ∑Zi分解
θ ( t + 1 ) = arg max θ ∑ k = 1 K ∑ i = 1 N log [ P k ⋅ N ( x i ∣ μ z , Σ k ) ] ⋅ P ( Z i = C k ∣ X i , θ ( t ) ) (19) \theta^{(t+1)}=\mathop{\arg\max}\limits_{\theta}\sum_{k=1}^K\sum_{i=1}^{N} \log [P_{k}·N(x_i|\mu_z,\Sigma_k)]·{P(Z_i=C_k|X_i,\theta^{(t)})} \tag{19} θ(t+1)=θargmaxk=1∑Ki=1∑Nlog[Pk⋅N(xi∣μz,Σk)]⋅P(Zi=Ck∣Xi,θ(t))(19)
θ ( t + 1 ) = arg max θ ∑ k = 1 K ∑ i = 1 N [ log P k + log N ( x i ∣ μ z , Σ k ) ] ⋅ P ( Z i = C k ∣ X i , θ ( t ) ) (20) \theta^{(t+1)}=\mathop{\arg\max}\limits_{\theta}\sum_{k=1}^K\sum_{i=1}^{N} [\log P_{k}+\log N(x_i|\mu_z,\Sigma_k)]·{P(Z_i=C_k|X_i,\theta^{(t)})} \tag{20} θ(t+1)=θargmaxk=1∑Ki=1∑N[logPk+logN(xi∣μz,Σk)]⋅P(Zi=Ck∣Xi,θ(t))(20)
我们求解的方式是通过不断地迭代求解相关参数:
θ ( t + 1 ) = { P 1 ( t + 1 ) , P 2 ( t + 1 ) , . . . , P k ( t + 1 ) , μ 1 ( t + 1 ) , μ 2 ( t + 1 ) , . . . , μ k ( t + 1 ) , Σ 1 ( t + 1 ) , Σ 2 ( t + 1 ) , . . . , Σ k ( t + 1 ) } (21) \theta^{(t+1)}=\{P_1^{(t+1)},P_2^{(t+1)},...,P_k^{(t+1)},\mu_1^{(t+1)},\mu_2^{(t+1)},...,\mu_k^{(t+1)},\Sigma_1^{(t+1)},\Sigma_2^{(t+1)},...,\Sigma_k^{(t+1)}\}\tag{21} θ(t+1)={P1(t+1),P2(t+1),...,Pk(t+1),μ1(t+1),μ2(t+1),...,μk(t+1),Σ1(t+1),Σ2(t+1),...,Σk(t+1)}(21)
对于公式(20)来说,当我们求解 P k ( t + 1 ) P_k^{(t+1)} Pk(t+1)时,我们可以把 log N ( x i ∣ μ z , Σ k ) \log N(x_i|\mu_z,\Sigma_k) logN(xi∣μz,Σk)看作无关项,可以忽略它。
P k ( t + 1 ) = arg max P k ∑ k = 1 K ∑ i = 1 N [ log P k ] ⋅ P ( Z i = C k ∣ X i , θ ( t ) ) (22) P_k^{(t+1)}=\mathop{\arg\max}\limits_{P_k}\sum_{k=1}^K\sum_{i=1}^{N} [\log P_{k}]·{P(Z_i=C_k|X_i,\theta^{(t)})} \tag{22} Pk(t+1)=Pkargmaxk=1∑Ki=1∑N[logPk]⋅P(Zi=Ck∣Xi,θ(t))(22)
s . t : ∑ k = 1 K P k = 1 (22) s.t: \sum_{k=1}^K P_k=1\tag{22} s.t:k=1∑KPk=1(22)
将上述带约束的最值问题转换成拉格朗日函数:
P ( L , λ ) = ∑ k = 1 K ∑ i = 1 N [ log P k ] ⋅ P ( Z i = C k ∣ X i , θ ( t ) ) + λ ( ∑ k = 1 K P k − 1 ) (23) P(L,\lambda)=\sum_{k=1}^K\sum_{i=1}^{N} [\log P_{k}]·{P(Z_i=C_k|X_i,\theta^{(t)})}+\lambda( \sum_{k=1}^K P_k-1)\tag{23} P(L,λ)=k=1∑Ki=1∑N[logPk]⋅P(Zi=Ck∣Xi,θ(t))+λ(k=1∑KPk−1)(23)
∂ P ( L , λ ) ∂ P k = ∑ i = 1 N 1 P k ⋅ P ( Z i = C k ∣ X i , θ ( t ) ) + λ = 0 (24) \frac{\partial P(L,\lambda)}{\partial P_k}=\sum_{i=1}^{N}\frac{1}{P_k}·{P(Z_i=C_k|X_i,\theta^{(t)})}+\lambda=0\tag{24} ∂Pk∂P(L,λ)=i=1∑NPk1⋅P(Zi=Ck∣Xi,θ(t))+λ=0(24)
∑ i = 1 N P ( Z i = C k ∣ X i , θ ( t ) ) + λ P k = 0 (25) \sum_{i=1}^{N}{P(Z_i=C_k|X_i,\theta^{(t)})}+\lambda P_k=0\tag{25} i=1∑NP(Zi=Ck∣Xi,θ(t))+λPk=0(25)
将 k=1,2,…K组成的等式进行求和可得:
∑ i = 1 N ∑ i = 1 K P ( Z i = C k ∣ X i , θ ( t ) ) ⏟ = 1 + λ ∑ i = 1 K P k ⏟ = 1 = 0 (26) \sum_{i=1}^{N}\underbrace{\sum_{i=1}^{K}{P(Z_i=C_k|X_i,\theta^{(t)})}}_{=1}+\lambda\underbrace{\sum_{i=1}^{K} P_k}_{=1}=0\tag{26} i=1∑N=1 i=1∑KP(Zi=Ck∣Xi,θ(t))+λ=1 i=1∑KPk=0(26)
N + λ = 0 → λ = − N (27) N+\lambda=0\rightarrow \lambda=-N\tag{27} N+λ=0→λ=−N(27)
将求得的 λ \lambda λ代入到公式25中可得:
∑ i = 1 N P ( Z i = C k ∣ X i , θ ( t ) ) − N P k = 0 (28) \sum_{i=1}^{N}{P(Z_i=C_k|X_i,\theta^{(t)})}-N P_k=0\tag{28} i=1∑NP(Zi=Ck∣Xi,θ(t))−NPk=0(28)
P k ( t + 1 ) = 1 N ∑ i = 1 N P ( Z i = C k ∣ X i , θ ( t ) ) (29) P_k^{(t+1)}=\frac{1}{N}\sum_{i=1}^{N}{P(Z_i=C_k|X_i,\theta^{(t)})}\tag{29} Pk(t+1)=N1i=1∑NP(Zi=Ck∣Xi,θ(t))(29)
所以我们能估算参数:
P k ( t + 1 ) = { P 1 ( t + 1 ) , P 2 ( t + 1 ) , . . . , P K ( t + 1 ) } (30) P_k^{(t+1)}=\{P_1^{(t+1)},P_2^{(t+1)},...,P_K^{(t+1)}\}\tag{30} Pk(t+1)={P1(t+1),P2(t+1),...,PK(t+1)}(30)
同理,我们只需要按照上述方式即可求得其他参数的估计值;后面再补充吧。
这篇关于21-高斯混合模型-GMM(Gaussian Mixture Model)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






