(二) 三维点云课程---GMM

1.前言

单变量高斯分布
$$\mathcal{N}\left(x\mid \mu ,{\sigma }^2\right)=\frac{1}{{\left(2\pi {\sigma }^2\right)}^{1/2}}\exp \left\{-\frac{1}{2{\sigma }^2}(x-\mu {)}^2\right\}$$

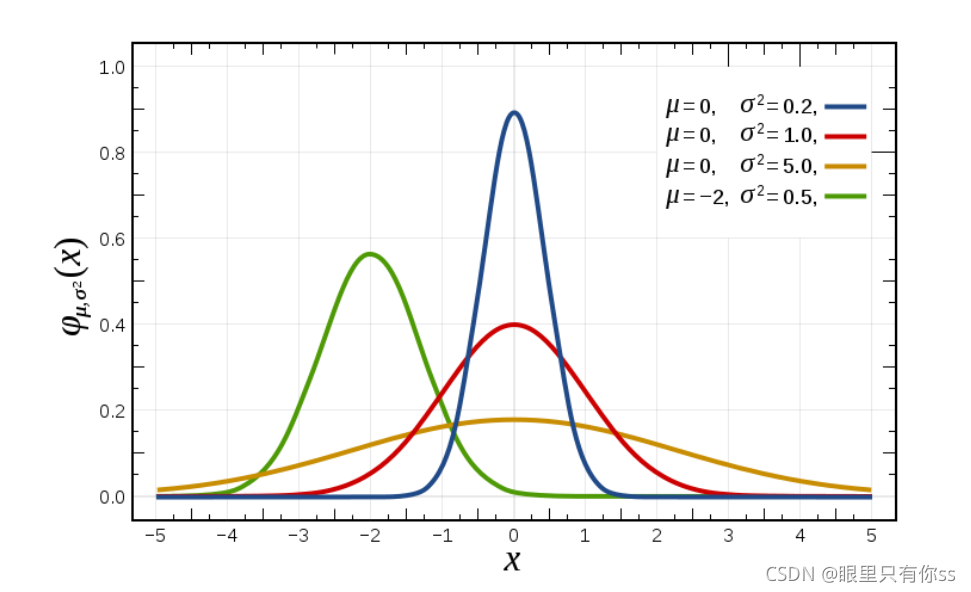
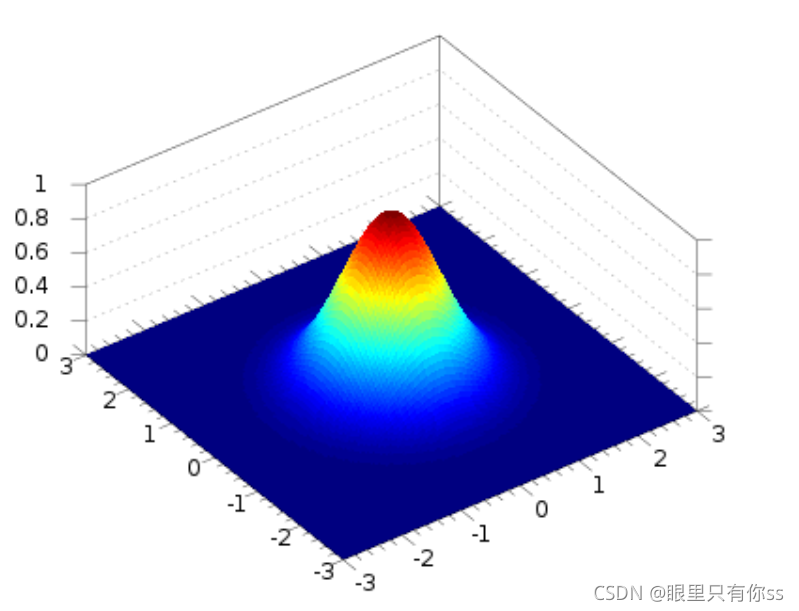
多变量的高斯分布，D是维数
$$\mathcal{N}(\mathbf{x}\mid \mathbf{\mu },\mathbf{\Sigma })=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\mathbf{\Sigma }{|}^{1/2}}\exp \left\{-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathbf{\mu })\right\}$$

2.GMM原理

2.1E步推导

对于一个混合高斯模型，可以写成多个单个高斯模型通过不同的权重进行叠加,其中${\pi }_k$表示权重
$$p(x)=\sum _{k=1}^K{\pi }_k\mathcal{N}\left(x\mid {\mu }_k,{\Sigma }_k\right)$$
现在引入一个K维二进制变量z,表达形式如下
z k ∈ { 0 , 1 } , Σ k z k = 1 z_k\in \{0,1\},\Sigma_{k} z_{k}=1 zk​∈{0,1},Σk​zk​=1
这$p(z_k=1)$是高斯分布$\mathcal{N}\left(x\mid {\mu }_k,{\Sigma }_k\right)$的先验概率,表达如下
$$p(z_k=1)={\pi }_k$$
先验的直观理解就是,不告诉我一个数据点在什么位置,只知道高斯模型的概率。以上式子有$0\le {\pi }_k\le 1,{\sum }_{k=1}^K{\pi }_k=1$的约束，联合起来，$p(z)$的表达如下
$$p(z)=\prod _{k=1}^K{\pi }_k^{z_k}$$
其中$z=[z_1,...,z_k,...,z_K]$。那么$p(x|z_k=1)$就坍塌成一个高斯分布了。
$$p\left(x\mid z_k=1\right)=\mathcal{N}\left(x\mid {\mu }_k,{\Sigma }_k\right)$$
所以$p(x|z)$表示如下
$$p(x\mid z)=\prod _{k=1}^K\mathcal{N}{\left(x\mid {\mu }_k,{\Sigma }_k\right)}^{z_k}$$
根据概率中的联合密度和边缘概率的关系$p(x)={\sum }_{z}p(x,z)$,可以得到
$$p(x)=\sum _{z}p(x,z)=\sum _{z}p(z)p(x|z)=\sum _z\prod _{k=1}^K{\pi }_k^{z_k}\prod _{k=1}^K\mathcal{N}{\left(x\mid {\mu }_k,{\Sigma }_k\right)}^{z_k}=\sum _{k=1}^K{\pi }_k\mathcal{N}\left(x\mid {\mu }_k,{\Sigma }_k\right)$$
根据贝叶斯概率分布公式可以得到
$$p(\mathbf{z}\mid \mathbf{x})=\frac{p(\mathbf{z},\mathbf{x})}{p(\mathbf{x})}=\frac{p(\mathbf{z})p(\mathbf{x}\mid \mathbf{z})}{{\sum }_{j=1}^{K}p\left(\mathbf{x}\mid z_j\right)p\left(z_j\right)}$$
令$\gamma (z_k)=p(z_k=1)$,那么
$$\begin{array}{rl}\gamma \left(z_k\right)\equiv p\left(z_k=1\mid \mathbf{x}\right)& =\frac{p\left(z_k=1\right)p\left(\mathbf{x}\mid z_k=1\right)}{{\sum }_{j=1}^{K}p\left(z_j=1\right)p\left(\mathbf{x}\mid z_j=1\right)}\\ & =\frac{{\pi }_k\mathcal{N}\left({\mathbf{x}}_n\mid {\mu }_k,{\Sigma }_k\right)}{{\sum }_{j=1}^K{\pi }_j\mathcal{N}\left({\mathbf{x}}_n\mid {\mu }_j,{\Sigma }_j\right)}\end{array}$$

物理意义

${\gamma }_{nk}=p(z_{nk}=1|x_n)$:一个点属于哪个类的可能性

2.2.M步推导

上式当我们知道 { π k , μ k , Σ k } \{\pi_k,\mu_k,\Sigma_k\} {πk​,μk​,Σk​}和$x$，我们可以得到$\gamma (z_k)$。但是实际是我只知道数据点$x_1,...,x_N$和聚类的个数，让我们来估计 { π k , μ k , Σ k } , γ ( z k ) \{\pi_k,\mu_k,\Sigma_k\},\gamma(z_k) {πk​,μk​,Σk​},γ(zk​),此时我们需要最大似然估计
$$\begin{array}{rl}p(\mathbf{x})& =\sum _{k=1}^K{\pi }_k\mathcal{N}\left(\mathbf{x}\mid {\mu }_k,{\Sigma }_k\right)\\ \ln p(\mathbf{X}\mid \pi ,\mu ,\Sigma )& =\sum _{n=1}^N\ln \left\{\sum _{k=1}^K{\pi }_k\mathcal{N}\left({\mathbf{x}}_{\mathbf{n}}\mid {\mu }_k,{\Sigma }_k\right)\right\}\end{array}$$
其中$X=[x_1,...,x_N]$,因此最大似然表达如下
$$\pi ,\mu ,\mathbf{\Sigma }=\underset{\pi ,\mu ,\mathbf{\Sigma }}{\mathrm{argmax}}\ln p(\mathbf{X}\mid \pi ,\mu ,\mathbf{\Sigma })=\underset{\pi ,\mu ,\mathbf{\Sigma }}{\mathrm{argmax}}\sum _{n=1}^N\ln \left\{\sum _{k=1}^K{\pi }_k\mathcal{N}\left({\mathbf{x}}_n\mid {\mu }_k,{\mathbf{\Sigma }}_k\right)\right\}$$
对于求解多个变量的最优问题，大多数是固定其中多个变量，只求解一个，进行迭代求解即可。

2.2.1固定${\pi }_k,{\Sigma }_k$,求解${\mu }_k$

对上式进行求导可知，省略求导过程
$$\begin{gathered} 0=-\sum _{n=1}^N\frac{{\pi }_k\mathcal{N}\left(x_n\mid {\mu }_k,{\Sigma }_k\right)}{{\sum }_j{\pi }_j\mathcal{N}\left(x_n\mid {\mu }_j,{\Sigma }_j\right)}{\Sigma }_K(x_n-{\mu }_k) \\ \iff 0=-\sum _{n=1}^N\gamma (z_{nk}){\Sigma }_K(x_n-{\mu }_k) \end{gathered}$$
化简得
$${\mu }_k=\frac{\sum _{n=1}^N\gamma (z_{nk})x_n}{N_k},N_k=\sum _{n=1}^N\gamma (z_{nk})$$
物理意义
$N_k$:分配给聚类K的有效点数，即有多个点属于k这个类

${\mu }_k$:所有点在k这个类上的加权平均，这个不同于KMeans简单的进行求平均，在这里引入了权重的概念

2.2.2固定${\pi }_k,{\mu }_k$,求解${\Sigma }_k$

求导过程省略
$${\Sigma }_k=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T，N_k=\sum _{n=1}^N\gamma (z_{nk})$$
物理意义

${\Sigma }_k$:是以${\mu }_k$为中心的所有点方差的加权平均值,权重为后验概率$\gamma (z_{nk})$

2.2.3固定${\mu }_k,{\Sigma }_k$，求解${\pi }_k$

解这个问题时，存在一个限制条件$\sum\nolimits_{k = 1}^K {{\pi _k} = 1} $。关于有限制条件的求导，使用拉格朗日求导法
$$\ln p(\mathbf{X}\mid \pi ,\mu ,\Sigma )+\lambda (\sum _{k=1}^K{\pi }_k-1)$$
对上式进行关于${\mu }_k$的求导
$$\sum _{n=1}^N\frac{\mathcal{N}\left(x_n\mid {\mu }_k,{\Sigma }_k\right)}{{\sum }_j{\pi }_j\mathcal{N}\left(x_n\mid {\mu }_j,{\Sigma }_j\right)}+\lambda =0$$
首先求解$\lambda$,等式两边同时乘以$\sum _{k=1}^K{\pi }_k$,化简得

$$\sum _{k=1}^K{\pi }_k\sum _{n=1}^N\frac{\mathcal{N}\left(x_n\mid {\mu }_k,{\Sigma }_k\right)}{{\sum }_j{\pi }_j\mathcal{N}\left(x_n\mid {\mu }_j,{\Sigma }_j\right)}+\sum _{k=1}^K{\pi }_k\lambda =0$$
$$\sum _{k=1}^K\frac{\sum _{n=1}^N{\pi }_k\mathcal{N}\left(x_n\mid {\mu }_k,{\Sigma }_k\right)}{{\sum }_j{\pi }_j\mathcal{N}\left(x_n\mid {\mu }_j,{\Sigma }_j\right)}+\sum _{k=1}^K{\pi }_k\lambda =0$$
$$\begin{gathered} (\sum _{n=1}^{N}1)+\lambda =0 \\ \lambda =-N \end{gathered}$$
再次将$\lambda$代入，进而求解${\pi }_k$
$$\begin{gathered} \sum _{n=1}^N\frac{\mathcal{N}\left(x_n\mid {\mu }_k,{\Sigma }_k\right)}{{\sum }_j{\pi }_j\mathcal{N}\left(x_n\mid {\mu }_j,{\Sigma }_j\right)}+\lambda =0 \\ \frac{1}{{\pi }_k}\sum _{n=1}^N\frac{{\pi }_k\mathcal{N}\left(x_n\mid {\mu }_k,{\Sigma }_k\right)}{{\sum }_j{\pi }_j\mathcal{N}\left(x_n\mid {\mu }_j,{\Sigma }_j\right)}-N=0 \\ \frac{1}{{\pi }_k}\sum _{n=1}^N{\gamma }_{nk}-N=0 \\ {\pi }_k=\frac{N_k}{N} \end{gathered}$$
物理意义

${\pi }_k$:表示的是实际上有多少个点属于我这个类$\div $所有点的数量

3.GMM总结

• 初始化每一个高斯模型的权重${\pi }_k$,均值${\mu }_k$和方差${\Sigma }_k$

  # π(alpha),初始化权重值，即初始时，平分权重
  alpha = np.ones(self.n_clusters) / self.n_clusters# μ(mu),随机初始化期望值
  mu = np.array([[.403, .237], [.714, .346], [.532, .472]])# ∑(sigma)，这是一个k*data.shape[1]*data.shape[1]三维矩阵，目的是一次性的将方差储存起来,其中初值为对角矩阵，
  # 这里以3*2*2，∑为[[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]]],第一块(sigma[0])为k=0对应的方差,同理第二块，第三块也是这样
  sigma = np.full((self.n_clusters, n_features, n_features), np.diag(np.full(n_features, 0.1)))
  

  其中 self.n_clusters表示为聚类的个数，n_features表示数据的列数，这里是2，数据是以N*2表示的

  
  

• E步:通过权重，均值，方差估计后验概率${\gamma }_{nk}=p(z_{nk}=1|x_n)$,表示一个点属于哪个类的可能性

  gamma = self.computeGamma(data, mu, sigma, alpha, self.multiGaussian)   #维数N*k
  

  计算$\gamma (z_{nk})$，调用computeGamma函数和multiGaussian函数，函数如下

  
  

  def computeGamma(self, X, mu, sigma, alpha, multiGaussian):n_samples = X.shape[0]n_clusters = len(alpha)gamma = np.zeros((n_samples, n_clusters))p = np.zeros(n_clusters)g = np.zeros(n_clusters)for i in range(n_samples):for j in range(n_clusters):p[j] = multiGaussian(X[i], mu[j], sigma[j])   #对应公式中的 N(xn|μj，∑j)g[j] = alpha[j] * p[j]                    #对应公式中的πj*N(xn|μj，∑j)for k in range(n_clusters):if np.sum(g)!=0:gamma[i, k] = g[k] / np.sum(g)            #对应公式的γnk的求解return gamma
  

  其中$p[j]$对应$\mathcal{N}\left(x\mid {\mu }_k,{\Sigma }_k\right)$,$g[j]$对应${\pi }_k\mathcal{N}\left(x\mid {\mu }_k,{\Sigma }_k\right)$
  
  

   def multiGaussian(self, x, mu, sigma):return 1 / ((2 * np.pi) * pow(np.linalg.det(sigma), 0.5)) * np.exp(-0.5 * (x - mu).dot(np.linalg.pinv(sigma)).dot((x - mu).T))
  

  对应于前言的多元高斯分布函数

  
  

• M步:计算最新的权重，均值，和方差
  $$\{\begin{array}{l}{\mu }_k=\frac{\sum _{n=1}^N\gamma (z_{nk})x_n}{N_k}\\ {\Sigma }_k=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T\\ {\pi }_k=\frac{N_k}{N}\\ N_k=\sum _{n=1}^N\gamma (z_{nk})\\ N=\sum _{n=1}^{N}1\end{array}$$
  计算权重

  alpha = np.sum(gamma, axis=0) / n_samples
  

  对应公式${\pi }_k=\frac{N_k}{N}$
  
  

  计算均值

  #更新均值 μ(mu)
  gamma_xn=data * gamma[:, i].reshape((n_samples, 1))  #维数N*k
  mu_molecule=np.sum(gamma_xn, axis=0)    #维数（k,）
  mu_denominator=np.sum(gamma, axis=0)[i]
  mu[i]=mu_molecule/mu_denominator
  

  其中gamma_xn表示$\gamma (z_{nk})x_n$,mu_molecule表示$\sum _{n=1}^N\gamma (z_{nk})x_n$,mu_denominator表示$N_k$
  
  

  计算协方差矩阵

  sigma[i] = 0
  for j in range(n_samples):#更新方差∑(sigma)xn_muk=data[j].reshape((1, n_features))-mu[i]    #维数 1*ksigma[i]+=(xn_muk).T.dot(xn_muk)*gamma[j,i]  #维数 k*k
  sigma[i] = sigma[i] / (np.sum(gamma, axis=0)[i])
  

  其中xn_muk表示为$x_n-{\mu }_k$。注意这里和公式不一样，是$(x_n-{\mu }_k{)}^T(x_n-{\mu }_k)$这样才可以表示为协方差矩阵，维数为2*2。

  
  

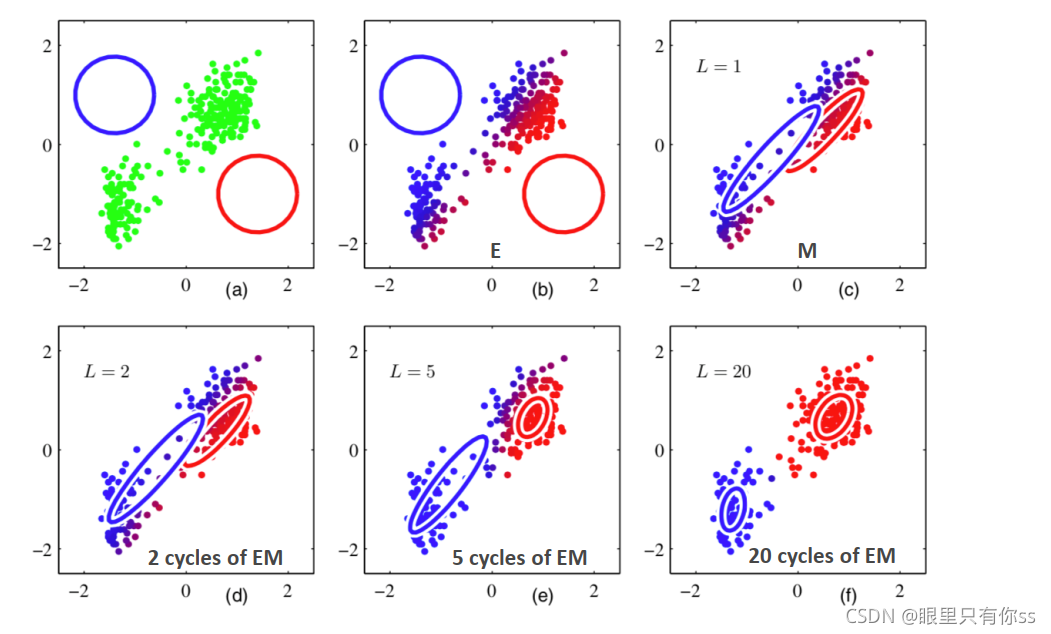
• 评估log函数的，如果收敛，则停止，否则返回到E步

效果如下，不同于KMeans的是，数据点有个渐变的过程，并不是非0即1

4.GMM完整代码

import numpy as np
from numpy import *
import pylab
import random, mathimport matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from scipy.stats import multivariate_normalplt.style.use('seaborn')class GMM(object):def __init__(self, n_clusters, max_iter=50):self.n_clusters = n_clusters         #聚类个数self.ITER = max_iter                 #最大迭代次数self.mu = 0                          #初始化均值self.sigma = 0                       #初始化协方差矩阵self.alpha = 0                       #初始化权重#计算多元高斯分布函数，注意这里是(x-mu)*sigma^(-1)*(x-mu)^T公式没有错，因为这里算出来的是一个数，并且不能直接运用在三维中，缺了个系数def multiGaussian(self, x, mu, sigma):return 1 / ((2 * np.pi) * pow(np.linalg.det(sigma), 0.5)) * np.exp(-0.5 * (x - mu).dot(np.linalg.pinv(sigma)).dot((x - mu).T))#计算后验概率γnk,维数为data.shape[0]*k,这里以k=2为例，第一列放的是所有属于k=0类的概率，第二列放的是所有属于k=1类的概率def computeGamma(self, X, mu, sigma, alpha, multiGaussian):n_samples = X.shape[0]n_clusters = len(alpha)gamma = np.zeros((n_samples, n_clusters))p = np.zeros(n_clusters)g = np.zeros(n_clusters)for i in range(n_samples):for j in range(n_clusters):p[j] = multiGaussian(X[i], mu[j], sigma[j])   #对应公式中的 N(xn|μj，∑j)g[j] = alpha[j] * p[j]                        #对应公式中的πj*N(xn|μj，∑j)for k in range(n_clusters):if np.sum(g)!=0:gamma[i, k] = g[k] / np.sum(g)            #对应公式的γnk的求解return gamma#GMM的核心代码def fit(self, data):n_samples = data.shape[0]n_features = data.shape[1]'''mu=data[np.random.choice(range(n_samples),self.n_clusters)]'''#初始化初值# π(alpha),初始化权重值，即初始时，平分权重alpha = np.ones(self.n_clusters) / self.n_clusters# μ(mu),随机初始化期望值mu = np.array([[.403, .237], [.714, .346], [.532, .472]])# ∑(sigma)，这是一个k*data.shape[1]*data.shape[1]三维矩阵，目的是一次性的将方差储存起来,其中初值为对角矩阵，# 这里以3*2*2，∑为[[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]],[[0.1,0],[0,0.1]]],第一块(sigma[0])为k=0对应的方差,同理第二块，第三块也是这样sigma = np.full((self.n_clusters, n_features, n_features), np.diag(np.full(n_features, 0.1)))for i in range(self.ITER):#E步，更新后验概率γnk，维数N*kgamma = self.computeGamma(data, mu, sigma, alpha, self.multiGaussian)   #M步，更新三大参数：权重，均值，方差#计算权重π(alpha)，维数1*kalpha = np.sum(gamma, axis=0) / n_samplesfor i in range(self.n_clusters):#计算均值 μ(mu)gamma_xn=data * gamma[:, i].reshape((n_samples, 1))  #维数N*kmu_molecule=np.sum(gamma_xn, axis=0)    #维数（k,）mu_denominator=np.sum(gamma, axis=0)[i]mu[i]=mu_molecule/mu_denominatorsigma[i] = 0for j in range(n_samples):#计算协方差矩阵∑(sigma)xn_muk=data[j].reshape((1, n_features))    #维数 1*k#维数 k*ksigma[i]+=(xn_muk-mu[i]).T.dot(xn_muk-mu[i])*gamma[j,i] sigma[i] = sigma[i] / (np.sum(gamma, axis=0)[i])self.mu = mu             #更新权重π(alpha)self.sigma = sigma       #更新均值μ(mu)self.alpha = alpha       #更新协方差矩阵∑(sigma)#GMM算法中的最终预测点的分类函数def predict(self, data):pred = self.computeGamma(data, self.mu, self.sigma, self.alpha, self.multiGaussian)cluster_results = np.argmax(pred, axis=1)return cluster_results##初始化画布为4行2列
fig, ax = plt.subplots(4, 2)
## 可视化函数
## 输入：x 原始数的路径
#        i 画布的行
#        j 画布的列
#        n_clusters 聚类的个数，认为指定
def show_result(x,i,j,n_clusters):ax[i][j].scatter(x[:, 0], x[:, 1], s=20, c="b", marker='o')ax[i][j].set_xlabel('x')ax[i][j].set_ylabel('y')gmm = GMM(n_clusters)gmm.fit(x)cat = gmm.predict(x)list_max = max(cat)if list_max == 1:for idx, value in enumerate(cat):if value == 0:ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="r", marker='*')elif value == 1:ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="g", marker='+')elif list_max == 2:for idx, value in enumerate(cat):if value == 0:ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="r", marker='*')elif value == 1:ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="g", marker='+')elif value == 2:ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="y", marker='^')ax[i][j+1].set_xlabel('x')ax[i][j+1].set_ylabel('y')## 读取数据的函数
def read_txt(path):filename = path  # txt文件和当前脚本在同一目录下，所以不用写具体路径pos = []Efield = []with open(filename, 'r') as file_to_read:while True:lines = file_to_read.readline()  # 整行读取数据if not lines:breakpassp_tmp, E_tmp = [float(i) for i in lines.split(",")]  # 将整行数据分割处理，如果分割符是空格，括号里就不用传入参数，如果是逗号， 则传入‘，'字符。pos.append(p_tmp)  # 添加新读取的数据Efield.append(E_tmp)passpos = np.array(pos)  # 将数据从list类型转换为array类型。Efield = np.array(Efield)x=np.vstack(pos)y=np.vstack(Efield)X=np.concatenate((x,y),axis=1)return Xif __name__ == '__main__':x_circle = read_txt("circle.txt")show_result(x_circle, 0, 0, 2)x_moons = read_txt("moons.txt")show_result(x_moons, 1, 0, 2)x_blobs = read_txt("varied.txt")show_result(x_blobs, 2, 0, 3)x_aniso = read_txt("aniso.txt")show_result(x_aniso, 3, 0, 3)plt.show()

仿真结果如下

数据集下载参见之前的KMeans文章

5.GMM的一些缺点

最大似然公式存在奇异性的问题：假设GMM的协方差矩阵为${\Sigma }_k={\sigma }_k^{2}I$,$I$为单位向量，有一个数据点$x_n={\mu }_j$,那么高斯分布为
$$\mathcal{N}\left(x\mid x_n,{\sigma }_j^{2}I\right)=\frac{1}{(2\pi {)}^{1/2}}\frac{1}{{\sigma }_j}$$
那么如果${\sigma }_j$非常小，高斯分布函数就非常大，系统可能会崩溃，例如如果一个点就是一个高斯分布，那么$\sigma =0$,N->0,$\prod p(x_i)$->0。因此，在GMM最大似然公式中，我们将高斯点放在单个点上，这会导致很大的问题。

解决方法：

1.采用MAP的方法，初始考虑${\mu }_k,{\Sigma }_k$，假如高斯分布的方差不能太小，就不会掉到奇点问题，但比较复杂

2.如果出现某个高斯点的方差很小，随机初始化另外的一个值。

其次GMM存在和KMeans同样的通病，需要人工给定聚类数。