convex专题

【Derivation】Convex Optimization

Separation theorems and supporting hyperplanes（分离定理与支撑超平面） Inner and outer polyhedral approximations.（内部与外部多面体逼近） Let C belongs to Rn be a closed convex set.and suppose that x1,...xk a

Convex Combination of Two Decision-Directed(DD)

双耦合判决引导 1、定义两个不同平滑参数的DD 其中，a >> b. 2、双耦合判决引导其中，论文中，a=0.99, b=0.6 在网上看到的一个关于DD优化的论文，文章据说可以优化音乐噪声和失真度。还没实际实现测试，攻关项目结束后跑个实际效果试试在把结果放这里。参考文献【1】A Priori SNR Estimator Based on a Convex Combinat

凸组合（convex combination）

假设x1,x2,...,xn是一组对象(要根据讨论问题的背景来确定)a1,a2,...,an是n个常数，并且满足a1+...+an=1,那么a1x1+...+anxn就称为x1,...,xn的凸组合

distance to convex cone

基本定义定义1：给定 1 ≤ K ≤ N 1 \leq K \leq N 1≤K≤N，定义凸锥(convex cone): D = { x ∣ 1 T x = 0 , x 1 : N − K ≤ 0 , x ∈ R N } \mathrm{D} = \{ \boldsymbol x | \boldsymbol 1^T \boldsymbol x =0, x_{1: N-K} \leq 0,

$凸包(Convex Hull)问题求解--Gift-Wrapping 算法$

凸包(Convex Hull)问题求解--Gift-Wrapping 算法

凸包问题（Convex Hull）求解--卷包裹(Gift-Wrapping) 算法 1.前言最近在做MIT 6.031的问题集0时遇到了要计算凸包的问题，题中提示要用Gift Wrapping算法。作为一个在实际工程中需要应用的求解算法来讲它并不是最好的，因为它有着的时间复杂度，但是我们依然可以通过它更好地理解问题的实质。更好地学习和应用这个基本算法。 2.Conv

HDU 3662 3D Convex Hull(三维凸包表面多边形个数）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3662 这个题目我的三维凸包模板竟然有问题，改后AC，模板题留个模板吧！ #include<iostream>#include<cmath>#include<cstring>#include<cstdlib>#include<algorithm>#include <stdio.h

权力的游戏：Curve上Yearn、Convex及Stake DAO之间的斗争

注：原文来自Rekt，以下为全文编译。不同的DeFi协议之间正在进行一场权力争夺战。 Yearn、Convex和Stake DAO正在为积累veCRV而战，力求在Curve Finance DAO上拥有权力和影响力，并最终能够为其用户提供更高的收益。这里的规则是，每个玩家必须通过向其用户提供具有吸引力的收益率来寻求增加TVL。为了提供最高的收益，每个玩家必须以veCRV代币的形式积累积

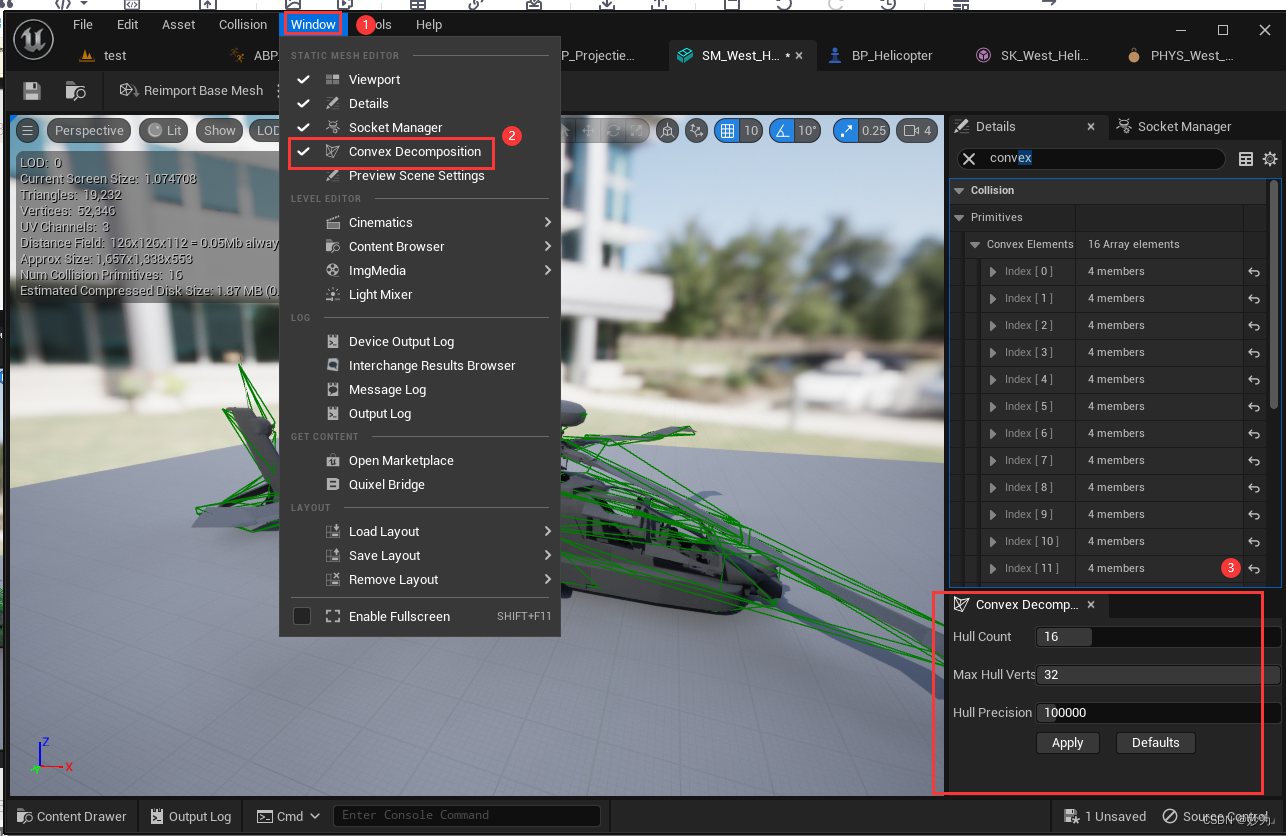
unreal engine5.1中设置convex decomposition凸包分解

UE5系列文章目录文章目录 UE5系列文章目录前言一、convex decomposition是什么？二、convex decomposition属性设置前言今天使用ue5根据网上教程制作可操控直升机，找属性convex decomposition凸包分解，默认的碰撞如下图如果想使用精细化的碰撞检测就要收到设置convex decomposition属性。如下图

Principal Convex Hull Analysis (PCHA) Method

代码：GitHub - ulfaslak/py_pcha: Python package that implements the PCHA algorithm for Archetypal Analysis by Mørup et. al. 论文举例： https://arxiv.org/pdf/1901.09078.pdf (PDF) Take ACTION to characte

Numerical Optimization和Convex optimization 两本书的选择?

Numerical Optimization和Convex optimization 两本书的选择? - 知乎https://www.zhihu.com/question/49689245 Numerical Optimization和Convex optimization 两本书的选择? 关注问题写回答

$凸集（convex set）$