Convex Optimization: 2 Convex sets 作业

2.8, 2.13, 2.22, A1.5, A1.9.

2.8

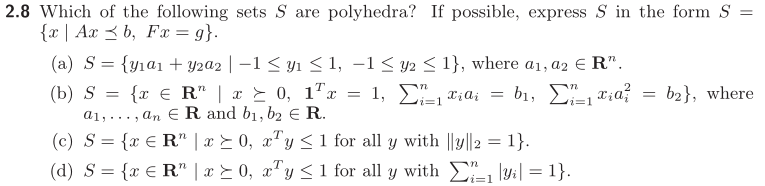
问以下哪些集合是多面体，如果可能的话，用 S = { x ∣ A x ⪯ b , F x = g } S=\{x|Ax\preceq b,Fx=g\} S={x∣Ax⪯b,Fx=g} 的形式来表示 $S$

a

$S$ 是一个多面体，它是由 $a_1+a_2,a_1-a_2,-a_1+a_2,-a_1-a_2$ 这四个顶点构成的，比如在 ${\mathbf{R}}^2$ 中：

集合 $S$ 可以描述为以下几个点集的交集：

• $S_1$ ：$a_1,a_2$ 所定义的平面上的点
• $S_2$： { z + y 1 a 1 + y 2 a 2 ∣ a 1 T z = a 2 T z = 0 , − 1 ≤ y 1 ≤ 1 } \{z+y_1a_1+y_2a_2|a_1^Tz=a_2^Tz=0,-1\le y_1\le 1\} {z+y1​a1​+y2​a2​∣a1T​z=a2T​z=0,−1≤y1​≤1}，其中 $z$ 是垂直于 $a_1,a_2$ 平面的向量，对于每一个固定的 $y_1$ ，$S_2$ 为一个平行于 $a_2$ 且垂直于 $a_1,a_2$ 所形成的平面的平面，变化 $y_1$，$S_2$ 实际上是一组这样的平面。
• $S_3$： { z + y 1 a 1 + y 2 a 2 ∣ a 1 z = a 2 T z = 0 , − 1 ≤ y 2 ≤ 1 } \{z+y_1a_1+y_2a_2|a_1z=a_2^Tz=0,-1\le y_2\le 1\} {z+y1​a1​+y2​a2​∣a1​z=a2T​z=0,−1≤y2​≤1} ，这个和 $S_2$ 同理，$S_3$ 平行于 $a_1$ ，垂直于 $a_1,a_2$ 所形成的平面，是一组平面。

以上三个集合取交集刚好是图中所示的平行四边形（阴影部分）

• $S_1$ 可以描述为：

$$v_k^{T}x=0,k=1,...,n-2$$

其中 $v_k$ 是垂直于 $a_1,a_2$ 的不相关的向量（矩阵 $[a_1,a_2{]}^T$ 的零空间（null space）），对于 ${\mathbf{R}}^2$ 来说这个面就不存在了，对于 ${\mathbf{R}}^3$ 及以上，这个就可以想象成 $a_1,a_2$ 形成的超平面。

• $S_2$ 可以描述为：

$$-|c_1^T{a}_1|\le c_1^{T}x\le |c_1^T{a}_1|$$

其中 $c_1=a_1-\frac{a_1^T{a}_2}{\Vert a_2{\Vert }_2^2}{a}_2$，这个可以理解为平行四边形的中心到右边的那个边做了一个垂线，中心到垂足形成的向量即为 $c_1$（不理解的话就画一画），$x$ 就是空间内任意一个向量，要满足的约束其实就是该向量和 $c_1$ 做内积的绝对值要小于等于 $\Vert c_1{\Vert }_2^2$ （$|c_1^T{a}_1|=\Vert c_1{\Vert }_2^2$，额不理解的话就画图），这整个的意思就是限制向量 $x$ 在平行四边形的左右两边之内。

$S_3$ 可以描述为：

$$-|c_2^T{a}_2|\le c_2^{T}x\le |c_2^T{a}_2|$$

其中 $c_2=a_2-\frac{a_2^T{a}_1}{\Vert a_1{\Vert }_2^2}{a}_1$，这个和 $S_2$ 的道理是一样的，意思是限制 $x$ 在平行四边形的上下两边内。

总和起来就可以得到 $2n$ 个线性不等式的约束：

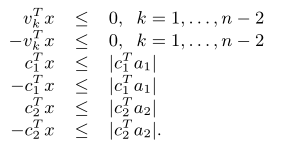
b

是一个多面体，$x$ 的每一个分量大于等于零，然后整体由三个等式约束。

c

不是一个多面体，它是单位球（ { x ∣ ∥ x ∥ 2 ≤ 1 } \{x|\|x\|_2\le 1\} {x∣∥x∥2​≤1}）和非负象限 ${\mathbf{R}}_{+}^n$ 的相交部分。根据柯西-施瓦茨不等式：

$$x^{T}y\le 1\text{ for all }y\text{ with }\Vert y{\Vert }_2=1⟺\Vert x{\Vert }_2\le 1$$

多面体的定义是多个半空间的相交部分，这里是无穷多个半平面的相交。

d

是一个多面体，$S$ 是集合 { x ∣ ∣ x k ∣ ≤ 1 , k = 1 , . . . , n } \{x||x_k|\le1,k=1,...,n\} {x∣∣xk​∣≤1,k=1,...,n} 与非负象限 ${\mathbf{R}}_{+}^n$ 的交集，即证明：

$$x^{T}y\le 1\text{ for all }y\text{ with }\sum _{i=1}^n|y_i|=1⟺|x_i|\le 1,i=1,...,n$$

首先假设 $|x_i|\le 1$ ，则有：

$$x^{T}y=\sum _i{x}_i{y}_i\le \sum _i|x_i||y_i|\le \sum _i|y_i|=1$$

然后再假设 $x$ 是一个满足 $x^{T}y\le 1,{\sum }_i|y_i|=1$ 的一个非零向量，令 $|x_k|={\max }_i|x_i|$ ，并令 $y_k{x}_k=|x_k|,y_i=0(i\ne k)$，则有：

$$x^{T}y=\sum _i{x}_i{y}_i=y_k{x}_k=|x_k|=\underset{i}{\max }|x_i|$$

即 ${\max }_i|x_i|\le 1$，因此可以用有限的线性不等式来表示 $S$，即为非负象限与 { x ∣ − 1 ⪯ x ⪯ 1 } \{x|-\mathbf{1}\preceq x\preceq\mathbf{1}\} {x∣−1⪯x⪯1} 之间的交集，即 $2n$ 个线性不等式的解：

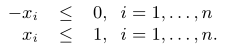
2.13

外积的圆锥壳：考虑秩为 $k$ 的外积的集合，定义为 { X X T ∣ X ∈ R n × k , r a n k X = k } \{XX^T|X\in\mathbf{R}^{n\times k},\mathbf{rank}\ X=k\} {XXT∣X∈Rn×k,rank X=k}。描述其圆锥壳。

首先可以知道 $X{X}^T⪰0$，并且 $\mathbf{r}\mathbf{a}\mathbf{n}\mathbf{k}(X{X}^T)=k$，也就是说题目中这个集合就是秩为 $k$ 的半正定矩阵的集合，先说答案：这个集合的圆锥壳是秩 $\ge k$ 的半正定矩阵集合再并上零矩阵。

一个集合的圆锥壳记为该集合元素的正组合，假设组合的秩 $<k$，即令 $A,B$ 为秩为 $k$ 的半正定矩阵，$\mathbf{r}\mathbf{a}\mathbf{n}\mathbf{k}(A+B)=r<k$，令 $V\in {\mathbf{R}}^{n\times (n-r)}$ 为 $A+B$ 零空间中的向量组成的矩阵，即 $\mathcal{R}(V)=\mathcal{N}(A+B)$，即：

$$V^T(A+B)V=V^{T}AV+V^{T}BV=0$$

又因为 $A,B⪰0$，因此 $V^{T}AV=V^{T}BV=0$，所以 $\mathbf{r}\mathbf{a}\mathbf{n}\mathbf{k}A\le r,\mathbf{r}\mathbf{a}\mathbf{n}\mathbf{k}B\le r$ ，与之前 $A,B$ 的秩为 $k$ 的假设矛盾！

因此该集合的的圆锥壳是秩 $\ge k$ 的半正定矩阵集合再并上零矩阵。

2.22

分离超平面定理（sepqrating hyperplane theorem）说的是：假设 $C,D$ 是非空的不相交的凸集，即 $C\cap S=\varnothing$，则存在 $a\ne 0,b$ 使得 $a^{T}x\le b,x\in C$ 以及 $a^{T}x\ge b,x\in D$ 成立。也就是说仿射函数 $a^{T}x-b$ 在 $C$ 上非正，在 $D$ 上非负。超平面 { x ∣ a T x = b } \{x|a^Tx=b\} {x∣aTx=b} 被称作 $C,D$ 的分离超平面，如下图所示：

在原始的证明中证明的是假如两个集合中存在某两个点的距离刚好等于两个集合的距离，那么这两个集合之间存在分离超平面，关键在于两个集合间距离的定义为：

d i s t ( C , D ) = i n f { ∥ u − v ∥ 2 ∣ u ∈ C , v ∈ D } \mathbf{dist}(C,D)=\mathrm{inf}\{\|u-v\|_2|u\in C,v\in D\} dist(C,D)=inf{∥u−v∥2​∣u∈C,v∈D}

其中 $\mathrm{i}\mathrm{n}\mathrm{f}$ 表示下确界，意思是小于等于集合中所有元素的最大值，对于明确存在最小值的集合来说，这个下确界就等于集合中的最小值，而对于开集来说，比如 { x ∣ 1 < x < 3 } \{x|1<x<3\} {x∣1<x<3} ，该集合的下确界就为 $1$ ，但是 $1$ 并不在这个集合中。所以书本中的证明只在 $C,D$ 是闭集，并且其中一个集合是有界的情况下才成立，这道题目要求证明的就是更加一般的情况，也就是考虑 $C,D$ 集合为开，在这两个集合中不能找出两个元素之间的距离刚好等于两个集合之间的距离。

要分成两种情况进行讨论：

1. 假设 $0\notin \mathbf{c}\mathbf{l}S$ ，即 $0$ 不在集合 $S$ 的闭包上，$S$ 的闭包指的是 $S$ 的内部点连通其边界上的点形成的集合，假如 $S$ 本身就是闭集，那么闭包就等于它自己，假如是开的，那么闭包就等于它自己并上它的边界。此时对集合 { 0 } \{0\} {0} 和 $\mathbf{c}\mathbf{l}S$ 应用已经证明过的部分，即在集合 { 0 } \{0\} {0} 和集合 $\mathbf{c}\mathbf{l}S$ 之间是存在分离超平面的（因为这两个集合都是闭集且其中有一个集合有界！），因此存在 $a\ne 0$ 使得
   $$a^T(x-y)>0$$
   对于所有 $x-y\in \mathbf{c}\mathbf{l}S$ 成立，因此对于所有 $x-y\in S$，$a^{T}x>a^{T}y$ 对于所有 $x\in C,y\in D$ 成立。

2. 假设 $0\in \mathbf{c}\mathbf{l}S$ ，由于 $0\notin S$ （两集合不相交），因此 $0$ 肯定在 $S$ 的边界上，因此这样一来我们就不能用第一种情况里的方法了，因为 $\mathbf{c}\mathbf{l}S$ 和 { 0 } \{0\} {0} 这两个集合是重叠的，无法应用书中已经证明的部分。再分情况进行讨论：假如 $S$ 的内部是空的，也就是说，他在一个超平面 { z ∣ a T z = b } \{z|a^Tz=b\} {z∣aTz=b} 中，又因为这个超平面通过原点，因此 $b=0$，因此对于所有 $x\in C,y\in D$，我们都有 $a^{T}x=a^{T}y$，这就是一个很 trivial 的分离超平面（这个例子可以脑补一下，就是两个集合 $C,D$ 是紧紧贴在这个超平面两侧的，他们中的元素无限接近这个超平面，但是永远到不了）；然后再假如 $S$ 的内部不空（也就是说这两个集合只有一小部分是相互无限贴近的，其他部分中间可以离得比较远。。脑补脑补），然后考虑集合 S − ϵ = { z ∣ B ( z , ϵ ) ⊆ S } S_{-\epsilon}=\{z|B(z,\epsilon)\sube S\} S−ϵ​={z∣B(z,ϵ)⊆S} ，其中 $B(z,ϵ)$ 是中心为 $z$ ，半径为 $ϵ>0$ 的欧几里得球，直观来讲，这个集合就是把原集合 $S$ 向里面收缩了 $ϵ$ ，这样得到的效果就是 $\mathbf{c}\mathbf{l}{S}_{-ϵ}$ 是闭集且凸，并且该集合不包含 $0$，因此我们就可以再愉快地用课本上已经证明过的部分啦，该集合可以用一个法线向量为 $a(ϵ)$ 的超平面与 { 0 } \{0\} {0} 分隔开：$a(ϵ{)}^{T}z>0\text{ for all }z\in S_{-ϵ}$ ，不失一般性，我们可以假设 $\Vert a(ϵ){\Vert }_2=1$。现在令 ${ϵ}_k,k=1,2,...$ 为一个正序列，并有 ${\lim }_{k\to \infty }{ϵ}_k=0$，由于 $\Vert a({ϵ}_k){\Vert }_2=1$ ，因此序列 $a({ϵ}_k)$ 是收敛的，定义这个序列最终可以收敛到 $\bar{a}$ ，于是对于所有的 $k$ 有 $a({ϵ}_k{)}^{T}z>0\text{ for all }z\in S_{-{ϵ}_k}$ ，因此对于所有 $z\in \mathbf{i}\mathbf{n}\mathbf{t}S$ 有 ${\bar{a}}^{T}z>0$，也就是对于所有的 $z\in S$ 有 ${\bar{a}}^{T}z\ge 0$ ，即对于所有的 $x\in C,y\in D$ 有 ${\bar{a}}^{T}x\ge {\bar{a}}^{T}y$ 。

A1.5

本题要证明两个闭凸锥交集的对偶等于各自对偶的和。即令 $C,D$ 为 ${\mathbf{R}}^n$ 上的闭凸锥，证明：

$$(C\cap D{)}^{\ast }=C^{\ast }+D^{\ast }$$

其中 $+$ 表示集合加法：$C^{\ast }+D^{\ast }$ 为 { u + v ∣ u ∈ C ∗ , v ∈ D ∗ } \{u+v|u\in C^*,v\in D^*\} {u+v∣u∈C∗,v∈D∗} ，证明步骤如下：

1. 证明 $C\cap D$ 和 $C^{\ast }+D^{\ast }$ 为凸锥（实际上，这两个是闭的，但是不要求证明）
2. 证明 $(C\cap D{)}^{\ast }\supseteq C^{\ast }+D^{\ast }$
3. 然后证明 $(C\cap D{)}^{\ast }\subseteq C^{\ast }+D^{\ast }$ ，证明思路是：首先证明
   $$(C\cap D{)}^{\ast }\subseteq C^{\ast }+D^{\ast }⟺C\cap D\supseteq (C^{\ast }+D^{\ast }{)}^{\ast }$$
   其中可以使用以下结论：如果 $K$ 是一个闭凸锥，那么 $K^{\ast \ast }=K$ ，之后再证明：$C\cap D\supseteq (C^{\ast }+D^{\ast }{)}^{\ast }$ ，最后得到结论 $(C\cap D{)}^{\ast }=C^{\ast }+D^{\ast }$
4. 证明多面体锥 V = { x ∣ A x ⪰ 0 } V=\{x|Ax\succeq0\} V={x∣Ax⪰0} 得对偶可以表示为：
   V ∗ = { A T v ∣ v ⪰ 0 } V^*=\{A^Tv|v\succeq0\} V∗={ATv∣v⪰0}

解答：

1. 证明 $C\cap D$ 和 $C^{\ast }+D^{\ast }$ 为凸锥：假设 $x\in C\cap D$ ，这意味着 $x\in C$ 且 $x\in D$ ，还意味着对于任意 $\theta \ge 0$ 来说， $\theta x\in C$ 以及 $\theta x\in D$ ，因此对于任意的 $\theta \ge 0$，有 $\theta x\in C\cap D$ ，故 $C\cap D$ 是一个锥，并且它是凸的，因为两个凸集的交集仍是凸集。为了证明 $C^{\ast }+D^{\ast }$ 是一个闭凸锥，注意到 $C^{\ast }$ 和 $D^{\ast }$ 都是凸锥，因此 $C^{\ast }+D^{\ast }$ 是 $C^{\ast }\cap D^{\ast }$ 的锥包，因此是一个凸锥。
2. 证明 $(C\cap D{)}^{\ast }\supseteq C^{\ast }+D^{\ast }$：假设 $x\in C^{\ast }+D^{\ast }$ ，我们可以把 $x$ 写成 $x=u+v$ ，其中 $u\in C^{\ast },v\in D^{\ast }$ ，根据对偶锥的定义，对于所有 $y\in C$ 有 $u^{T}y\ge 0$，对于所有 $y\in D$ 有 $v^{T}y\ge 0$ ，可以推出对于所有 $y\in C\cap D$ 有 $x^{T}y=u^{T}y+v^{T}y\ge 0$ ，这意味着 $x\in (C\cap D{)}^{\ast }$ ，因此 $(C\cap D{)}^{\ast }\supseteq C^{\ast }+D^{\ast }$
3. 证明 $(C\cap D{)}^{\ast }\subseteq C^{\ast }+D^{\ast }$：已经证过 $C\cap D$ 和 $C^{\ast }+D^{\ast }$ 是闭凸锥，这意味着 $(C\cap D{)}^{\ast \ast }=C\cap D$ ，因此有：
   $$(C\cap D{)}^{\ast }\subseteq C^{\ast }+D^{\ast }⟺C\cap D\supseteq (C^{\ast }+D^{\ast }{)}^{\ast }$$
   假设 $x\in (C^{\ast }+D^{\ast }{)}^{\ast }$，则对于所有 $y=u+v$ 有 $x^{T}y\ge 0$，其中 $u\in C^{\ast },v\in D^{\ast }$ ，可以写为对于所有的 $u\in C^{\ast },v\in D^{\ast }$ 有 $x^{T}u+x^{T}v\ge 0$ 。因为 $0\in C^{\ast }$ 并且 $0\in D^{\ast }$ ，令 $v=0$，则对于所有的 $u\in C^{\ast }$ 有 $x^{T}u\ge 0$，令 $u=0$，则对于所有的 $v\in D^{\ast }$ 有 $x^{T}v\ge 0$。这样可以推出 $x\in C^{\ast \ast }=C$ 并且 $x\in D^{\ast \ast }=D$ ，即 $x\in C\cap D$ 。因此原式证毕。
4. 证明多面体锥 V = { x ∣ A x ⪰ 0 } V=\{x|Ax\succeq0\} V={x∣Ax⪰0} 的对偶可以表示为： V ∗ = { A T v ∣ v ⪰ 0 } V^*=\{A^Tv|v\succeq0\} V∗={ATv∣v⪰0}：使用本题证明的式子，可以得到：
   V ∗ = { x ∣ a 1 T x ≥ 0 } ∗ + ⋯ + { x ∣ a m T x ≥ 0 } ∗ V^*=\{x|a_1^Tx\ge0\}^*+\cdots+\{x|a_m^Tx\ge0\}^* V∗={x∣a1T​x≥0}∗+⋯+{x∣amT​x≥0}∗
   其中 { x ∣ a i T x ≥ 0 } \{x|a_i^Tx\ge0\} {x∣aiT​x≥0} 的对偶是集合 { θ a i ∣ θ ≥ 0 } \{\theta a_i|\theta\ge0\} {θai​∣θ≥0} （注：其中 $\theta$ 为常数，半平面的对偶是法线所在的射线，脑补一下~），因此我们得到：
   V ∗ = { θ a 1 ∣ θ ≥ 0 } + ⋯ + { θ a m ∣ θ ≥ 0 } = { θ 1 a 1 + ⋯ + θ m a m ∣ θ i ≥ 0 , i = 1 , . . . , m } = { A T θ ∣ θ ⪰ 0 } \begin{aligned} V^*&=\{\theta a_1|\theta\ge0\}+\cdots+\{\theta a_m|\theta\ge0\}\\ &=\{\theta_1a_1+\cdots+\theta_ma_m|\theta_i\ge0,i=1,...,m\}\\ &=\{A^T\mathbf{\theta}|\theta\succeq0\} \end{aligned} V∗​={θa1​∣θ≥0}+⋯+{θam​∣θ≥0}={θ1​a1​+⋯+θm​am​∣θi​≥0,i=1,...,m}={ATθ∣θ⪰0}​
   即： V ∗ = { A T v ∣ v ⪰ 0 } V^*=\{A^Tv|v\succeq0\} V∗={ATv∣v⪰0} （妙啊！）

A1.9

确定以下 ${\mathbf{S}}^n$ 的子集是否为凸集：

(a) 相关矩阵的集合： C n = { C ∈ S + n ∣ C i i = 1 , i = 1 , . . . , n } \mathcal{C}^n=\{C\in\mathbf{S}_+^n|C_{ii}=1,i=1,...,n\} Cn={C∈S+n​∣Cii​=1,i=1,...,n}

(b) 非负相关矩阵的集合： { C ∈ C n ∣ C i j ≥ 0 , i , j = 1 , . . . , n } \{C\in\mathcal{C}^n|C_{ij}\ge0,i,j=1,...,n\} {C∈Cn∣Cij​≥0,i,j=1,...,n}

(c) 高相关性的相关矩阵的集合： { C ∈ C n ∣ C i j ≥ 0.8 , i , j = 1 , . . . , n } \{C\in\mathcal{C}^n|C_{ij}\ge0.8,i,j=1,...,n\} {C∈Cn∣Cij​≥0.8,i,j=1,...,n}

(a) 令 $X\in {\mathcal{C}}^n,Y\in {\mathcal{C}}^n$, 因此有 $X\in {\mathbf{S}}_{+}^n$ （也就是说 $X$ 是一个半正定矩阵），并且 $X_{ii}=1,i=1,...,n$，而且 $Y\in {\mathcal{S}}_{+}^n,Y_{ii}=1,i=1,...,n$ ，考虑 $Z=\theta X+(1-\theta )Y,\theta \in [0,1]$，显然 $Z\in {\mathbf{S}}_{+}^n$ （因为 ${\mathcal{S}}_{+}^n$ 是凸的），并且也显然有 $Z_{ii}=1,i=1,...,n$ ，因此有 $Z\in {\mathcal{C}}^n$ ，故 ${\mathcal{C}}^n$ 是凸集。

(b) 同理，令 $X,Y$ 都在这个集合内，考虑 $Z=\theta X+(1-\theta )Y,\theta \in [0,1]$，由于已经证过 ${\mathcal{C}}^n$ 为凸集，因此 $Z\in {\mathcal{C}}^n$ ，只需再验证 $Z_{ij}\ge 0,i,j=1,...,n$ 是否成立，显然成立（因为 $X_{ij}\ge 0,Y_{ij}\ge 0,i=1,...,n$） ，因此该集合也是凸集。

(c) 这个集合也是凸集，证明方法类似于 (b)，不再赘述（手动狗头）