bellman专题
poj 3259 uva 558 Wormholes(bellman最短路负权回路判断)
poj 3259: 题意:John的农场里n块地,m条路连接两块地,w个虫洞,虫洞是一条单向路,不但会把你传送到目的地,而且时间会倒退Ts。 任务是求你会不会在从某块地出发后又回来,看到了离开之前的自己。 判断树中是否存在负权回路就ok了。 bellman代码: #include<stdio.h>const int MaxN = 501;//农场数const int
Bellman_Ford变形求最长路+正权回路或spfa——POJ 1860
对应POJ题目:点击打开链接 Currency Exchange Time Limit: 1000MS Memory Limit: 30000KTotal Submissions: 20814 Accepted: 7451 Description Several currency exchange points are working in our city. L
Bellman-Ford算法模板题——POJ 3259
对应POJ题目:点击打开链接 Wormholes Time Limit:2000MS Memory Limit:65536KB 64bit IO Format:%I64d & %I64u Submit Status Practice POJ 3259 Description While exploring his many farms, F
深入理解Bellman-Ford算法:求解单源最短路径问题
深入理解Bellman-Ford算法:求解单源最短路径问题 在C++面试中,考官通常会关注候选人的编程能力、问题解决能力以及对C++语言特性的理解。Bellman-Ford算法是一个经典的图算法,用于求解单源最短路径问题,特别适用于含有负权边的图。本文将详细介绍如何在C++中实现Bellman-Ford算法,并探讨其应用和优化方法。 目录 引言Bellman-Ford算法简介算法步骤实现步骤
算法训练营|图论第10天 Bellman_ford:优化算法,判断负权算法,单源有限最短路
题目:Bellman_ford:优化算法 题目链接: 94. 城市间货物运输 I (kamacoder.com) 代码: #include<bits/stdc++.h>using namespace std;struct Edge {int to;int val;Edge(int t, int w) :to(t), val(w) {}};int main() {int n, m;c
最短路算法详解(Dijkstra 算法,Bellman-Ford 算法,Floyd-Warshall 算法)
文章目录 一、Dijkstra 算法二、Bellman-Ford 算法三、Floyd-Warshall 算法 由于文章篇幅有限,下面都只给出算法对应的部分代码,需要全部代码调试参考的请点击: 图的源码 最短路径问题:从在带权图的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。涉及到三个算法: 单源最短路径:Dijkstra 算法(迪杰斯
算法工程师第五十一天(dijkstra(堆优化版)精讲 Bellman_ford 算法精讲)
参考文献 代码随想录 一、参加科学大会 题目描述 小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。 小明的起点是第一个车站,终点是最后一个车站。然而,途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素(如天气变化)等不同,这些因素都会影响每条路径的通行时间。 小明希望能选择一条花费时间最少的路线,以确保他能够尽快到达目的地。 输入描述 第一行包
【深入解析】最优控制中的Bellman方程——从决策到最优路径的探索
【深入解析】最优控制中的Bellman方程——从决策到最优路径的探索 关键词提炼 #Bellman方程 #最优控制 #动态规划 #值函数 #策略优化 #强化学习 第一节:Bellman方程的通俗解释与核心概念 1.1 通俗解释 Bellman方程是动态规划中的一个核心概念,它像是一个“未来价值指南针”,帮助我们在面对一系列决策时,找到从当前状态出发到达目标状态的最优路径。想象一下,你站
单源点最短路径Bellman算法实现
一、数据集形式 其中:6105(节点个数) 7035(边数) 0(id) 1609(起始边) 1622(终边) 57.403187(权重) 二、数据集 数据集下载链接 三、实现代码 #include "stdafx.h"#include "time.h"#include <fstream>#include<iostream>#include <stack>#includ
HDU 1317 XYZZY Bellman-Ford求最长路 判断正环
题意:给你n个房间 开始有能量值100 判断能否从1到第n个房间 每到一个房间可以获得能量x(可能小于0) 每到一个房间总能量必须大于0 每个房间可以重复到达 思路:求一个从1到n的最长路 不过可能有正环 没有正环 直接求最长路 如果有正环 判断环中的点是否可以到达n 具体用Bellman-Ford算法 虽然复杂度是(n*m)这题应该可以了 如果迭代n-1次之后还能松弛 说明有正环 然后
最短路径Bellman-Ford算法和SPFA算法详解
目录 Bellman-Ford算法介绍 Bellman-Ford算法证明 Bellman-Ford算法实现 SPFA算法详解 Bellman-Ford算法介绍 Dijkstra算法可以很好的解决无负权图的最短路径问题,但是如果出现了负权边,Dijkstra算法就会失效。为了更好地求解有负权边的最短路径问题,需要使用Bellman-Ford算法(简称BF算法)。和Dijkstra算法一样
最短路:Bellman-Ford
最短路:Bellman-Ford 题目描述参考代码 题目描述 输入样例 3 3 11 2 12 3 11 3 3 输出样例 3 参考代码 #include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N = 510, M = 10010;in
Bellman-Ford算法寻找最短路径可用于计算机网络
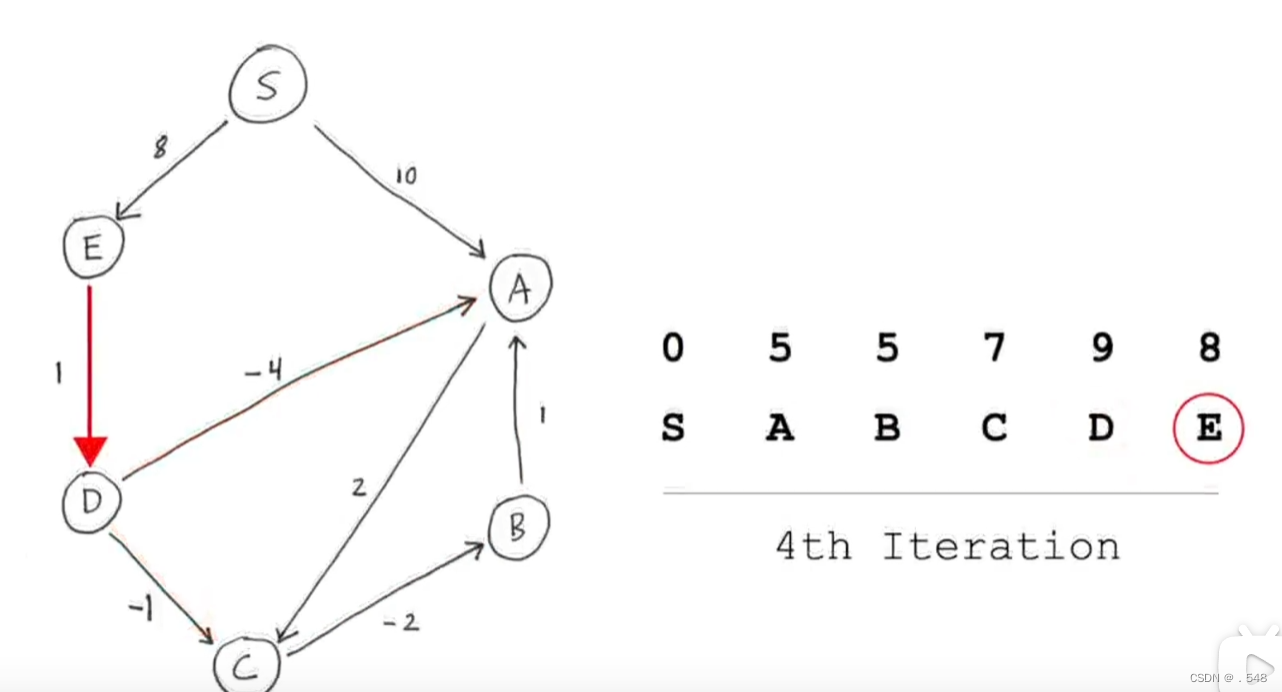
从s开始看指向别的节点的边 s有两条边,一条指向E,另外一条指向A,更新表中s与A和E的距离 然后从A开始看指向别的节点的边,指向C的边,加上s到A的距离就是s到C的距离并更新表中C的数据 然后从B开始,但是我们发现暂时没有到B的边,所以先跳过B 从C开始,只有一条指向B的边,加上从s到C的距离就是s到B的距离并更新表中B的数据 从D开始,我们暂时没有发现到D的路径,于
POJ - 3259 Wormholes(判断负环, Bellman Ford,SPFA)
虫洞能够时光倒流,判断能否在回到出发的位置的时候在出发的时候之前。(判断是否存在负环) 初学最短路,尝试着用了三种方法判断: 1、Bellman Ford (令d全部为0,仅用来判断负环) OJ测试得157MS 2、Bellman Ford 结束后再来一轮松弛若松弛成功则存在负环。 235MS 3、Bellman Ford 用队列优化过的SPFA,判断是否存在一个点同队大
最短路径算法 dijkstra bellman-ford floyd
Dijkstra算法: 1.定义概览 Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。注意该算法要求图中不存在负权边。 问题描述:在无向图 G=(V,
算法学习笔记(最短路——Bellman-Ford)
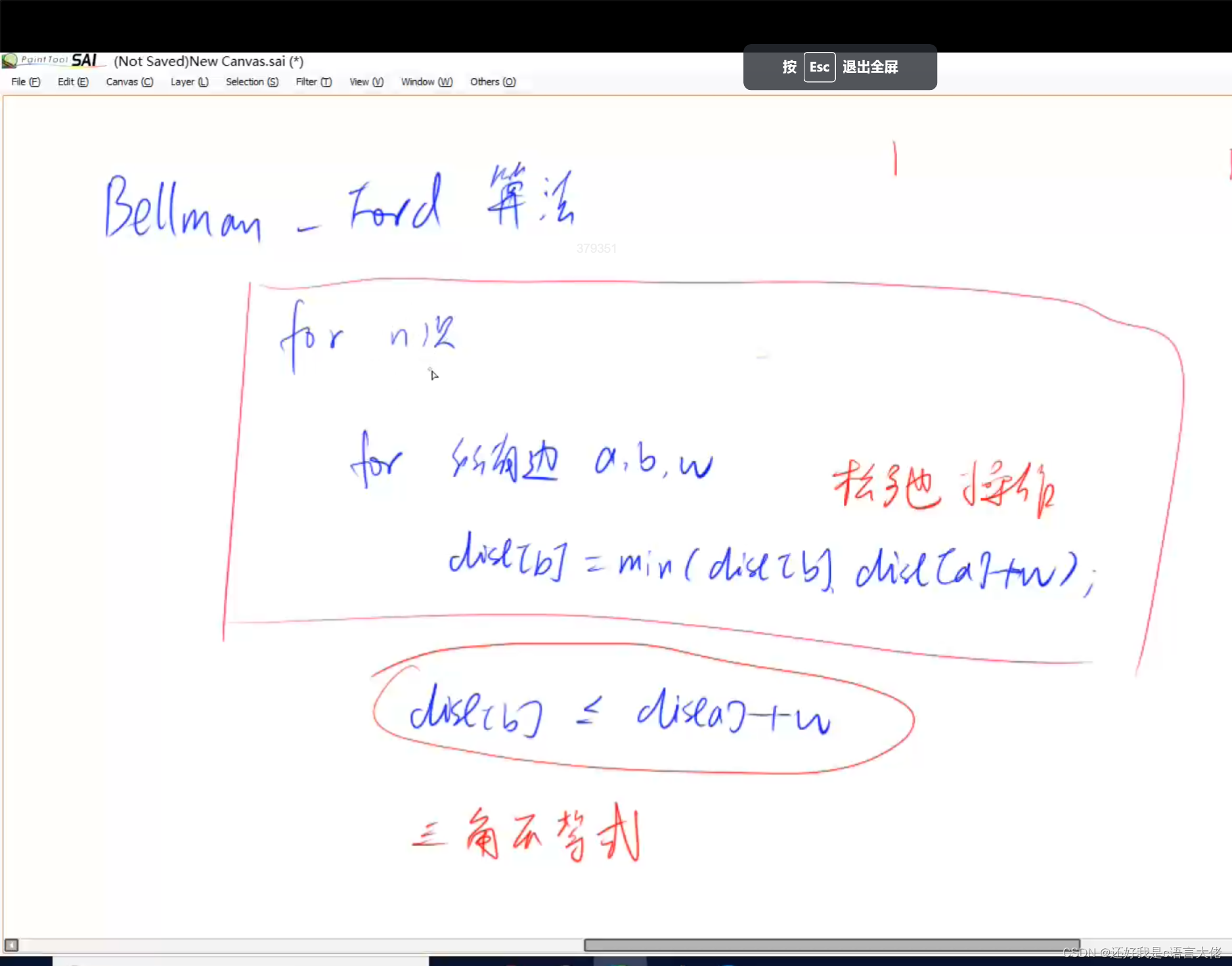
B e l l m a n — F o r d Bellman—Ford Bellman—Ford是一种单源最短路径算法,可以用于边权为负的图,但是只能用于小图。 大概过程: 枚举每一条边,更新可以更新的节点(起点到自己距离为 0 0 0,从地点开始向外)。重复第一个步骤 n − 1 n - 1 n−1次(起点不用),每一轮至少有一个节点会被更新出最短路径(和 D i j k s t r a
最短路(Dijkstra, Bellman-Ford, SPFA, Floyd)
最短路 Dijkstra算法(复杂度 O ( m l o g n ) O(mlog n) O(mlogn)/ O ( n m l o g n ) O(nmlogn) O(nmlogn))–不能有负权边,不能有负权环,单源最短路径( O ( m l o g n ) O(mlog n) O(mlogn)),多源最短路径( O ( n m l o g n ) O(nmlogn) O(nmlogn))。
数据结构:最小生成树(Prim算法和Kruskal算法)、图的最短路径(Dijkstra算法和Bellman-Ford算法)
什么是最小生成树?Prim算法和Kruskal算法是如何找到最小生成树的? 最小生成树是指在一个连通图中,通过连接所有节点并使得总权重最小的子图。 Prim算法和Kruskal算法是两种常用的算法,用于寻找最小生成树。 Prim算法的步骤如下: i. 选择一个起始节点,将其标记为已访问。 ii. 初始化一个空的最小生成树集合和一个优先队列(一般使用最小堆),用于存储边。 iii. 将起
Bellman-Ford算法和SPFA算法以及Floyd算法学习心得
对于BF算法,我们主要是用于解决Dijkstra算法不能解决的问题,我们之前说到,Dijkstra算法的使用范围是结点之间的边权为正数的情况。所以BF算法可以解决边权为负的情况。 我们考虑环的问题,我们可以知道,如果某个点经过一系列的点后回到自身后,如果边权之和为正的话,则称为正环,为0则为零环,为负则为负环。对于正环和零环的情况,我们可以知道不会影响最短路径的取值,但是如果出现负环,我们的算法就
HDU - 2680 Choose the best route(Bellman-Ford)
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=2680 Problem Description One day , Kiki wants to visit one of her friends. As she is liable to carsickness , she wants to arrive at her friend’s home as
[算法与数据结构] - No.10 图论(3)- 最短路Dijkstra算法、Bellman-Ford算法和Floyd算法
最短路径问题:如果从图中某一顶点(称为源点)到达另一顶点(称为终点)的路径可能不止一条,如何找到一条路径使得沿此路径上各边上的权值总和达到最小。 三种算法主要用途: 1. 边上权值非负情形的单源最短路径问题 — Dijkstra算法 2. 边上权值为任意值的单源最短路径问题 — Bellman和Ford算法 3. 所有顶点之间的最短路径 — Floyd算法 Dijkstra
BellMan-Ford算法--寻找最短路径
## 序言 ## Bellman-Ford算法解决的是一般情况下的单元最短路径问题,在这里,边的权重可以为赋负值,在给定带权重的有向图G=(V,E)和权重函数w:E->,Bellman-Ford 算法返回一个布尔值,以表明是否存在从源节点可以到达的权重为负值的环路。那么如果存在这样一个环路,算法将告诉我们不存在解决方案,如果没有这种环路存在,算法将给出最短路径和它们的权重。 Bellman-
AcWing853.有边数限制的最短路(Bellman_ford算法)
【题目链接】853. 有边数限制的最短路 - AcWing题库 【题目描述】 输入样例: 3 3 11 2 12 3 11 3 3 输出样例: 3 【代码及详细注释】 #include<bits/stdc++.h>using namespace std;const int N=1e4+10;struct node{int a,b,w;//表示每条边的起点终点和边长
搜索与图论——bellman—ford算法、spfa算法求最短路
bellman-ford算法 时间复杂度O(nm) 在一般情况下,spfa算法都优于bf算法,但遇到最短路的边数有限制的题时,只能用bf算法 bf算法和dijkstra很像 #include<iostream>#include<queue>#include<cstring>#include<algorithm>using namespace std;const int N = 51
poj 3259 Wormholes SPFA // Bellman-ford
//最水的模版题,记下来以后忘了可以看看。 //SPFA #include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; const int INF=0x3f3f3f3f; const int maxn=505; int n, m, w, d[maxn], inqueue[ma
图论-最短路(bellman-fod算法)
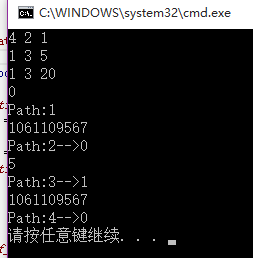
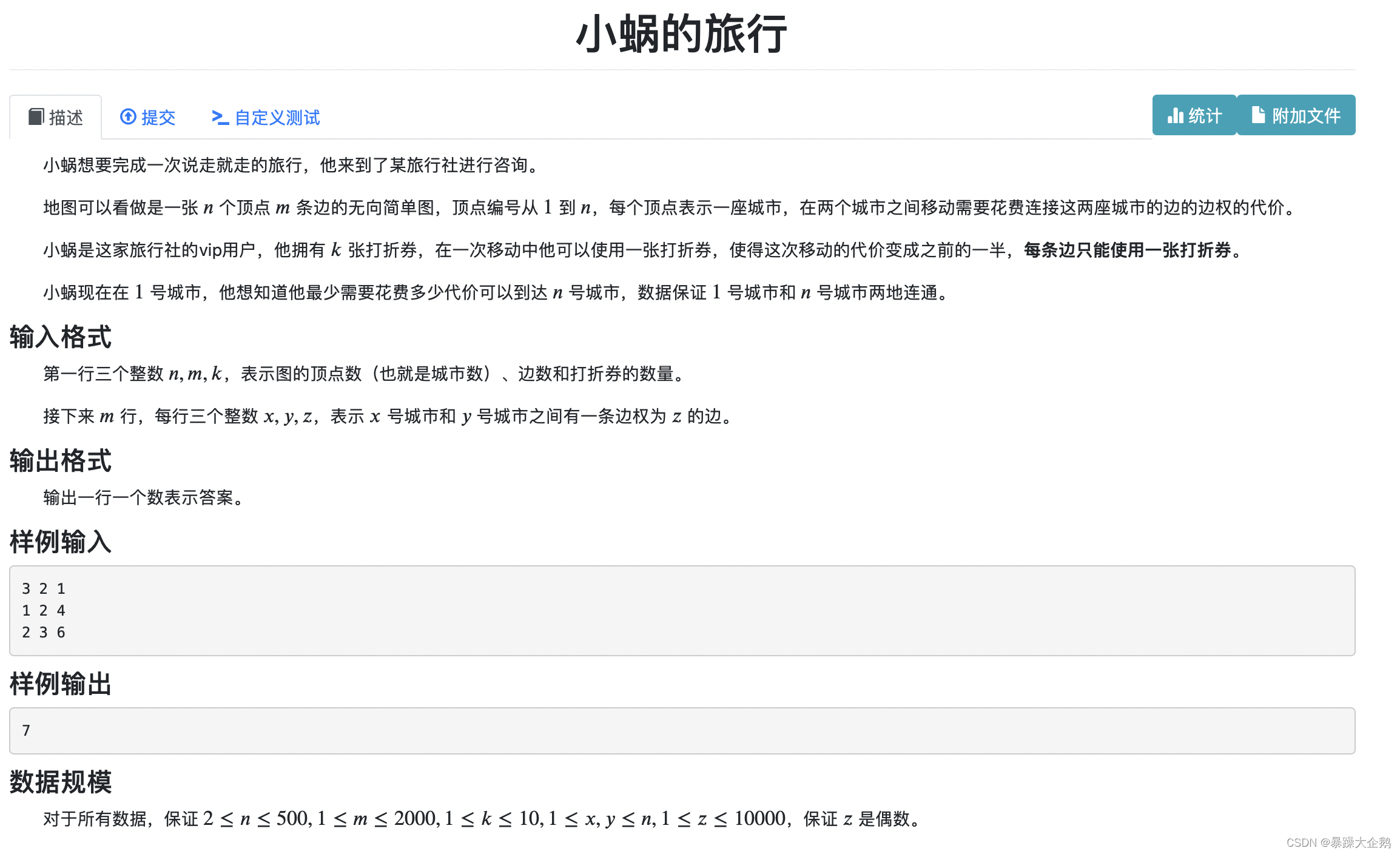
目录 目录 1.最短路 2.最短路pro(要求求出最短路径上的点,其余条件和第一问完全相同) 3.租房 4.小蜗的旅行 1.最短路 2.最短路pro(要求求出最短路径上的点,其余条件和第一问完全相同) //最短路2(求最短距离及其路径)#include <bits/stdc++.h>using namespace std;int n, m, k;struct no



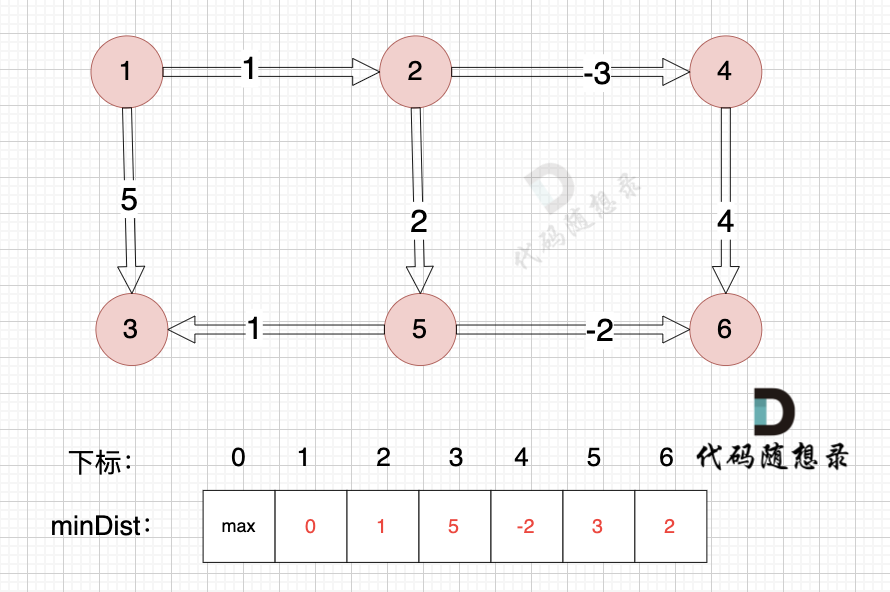




![[算法与数据结构] - No.10 图论(3)- 最短路Dijkstra算法、Bellman-Ford算法和Floyd算法](https://img-blog.csdn.net/20170804230334783?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdGp1eWFubWluZw==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)