图论-最短路（bellman-fod算法）

目录

目录

1.最短路

2.最短路pro（要求求出最短路径上的点，其余条件和第一问完全相同）

3.租房

4.小蜗的旅行 

1.最短路

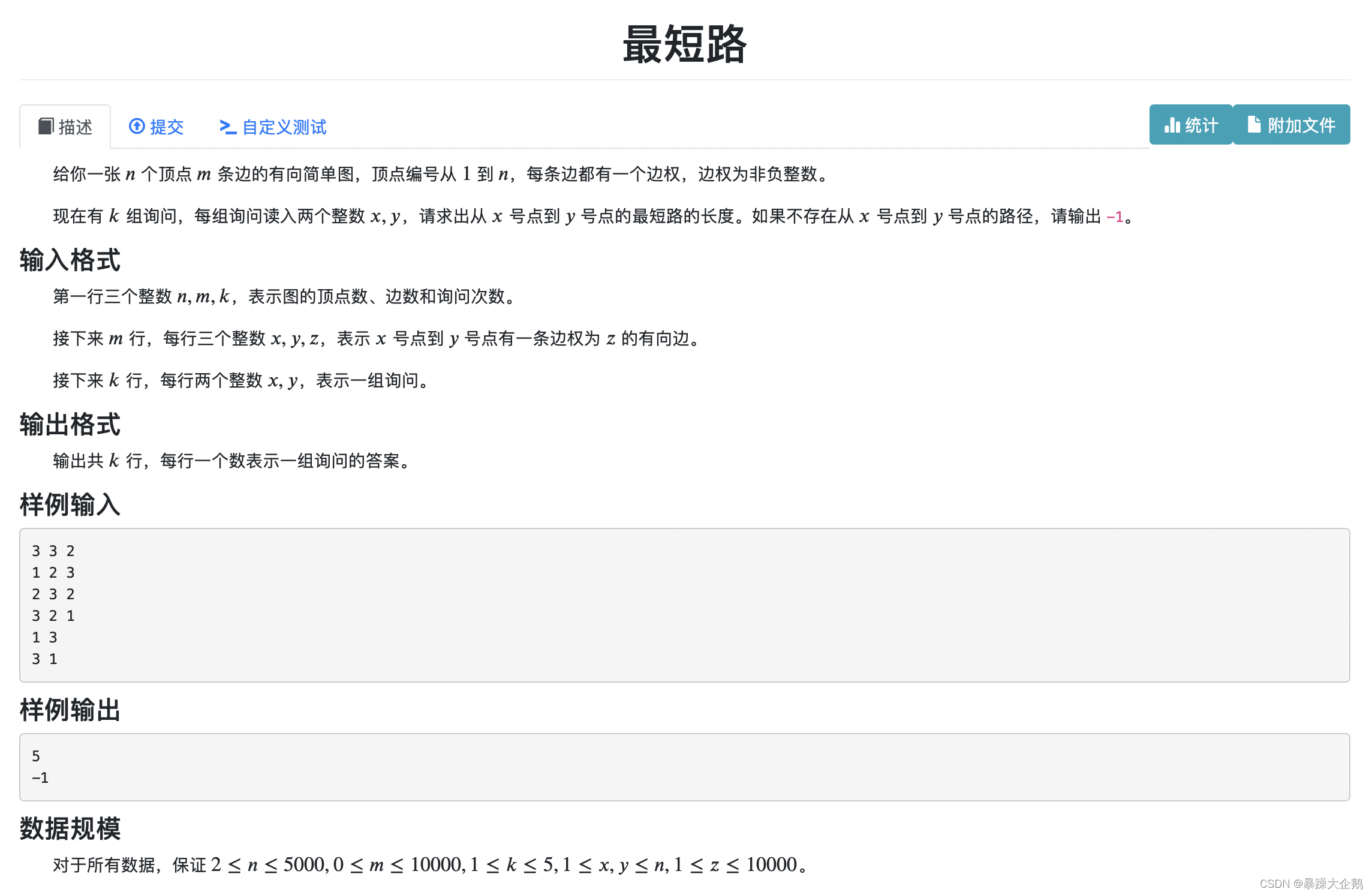
2.最短路pro（要求求出最短路径上的点，其余条件和第一问完全相同）

//最短路2（求最短距离及其路径）
#include <bits/stdc++.h>
using namespace std;
int n, m, k;
struct node {int x, y, v;
} edges[10001];
int dis[5001], pre[5001], path[5001];inline void bellmanFod(int s, int f) {memset(dis, 127, sizeof(dis));memset(pre, 127, sizeof(pre));dis[s] = 0;while (1) {bool ok = 0;for (int i = 1; i <= m; i++) {int x = edges[i].x, y = edges[i].y, v = edges[i].v;if (dis[x] < 1 << 30) {if (dis[x] + v < dis[y]) {dis[y] = dis[x] + v;pre[y] = x;ok = 1;}}}if (!ok) {break;}}if (dis[f] < 1 << 30) {cout << dis[f] << '\n';int l = 0;for (int i = f; i != s; i = pre[i]){path[++l] = i;}path[++l] = s;for (int i = l; i; i--) {cout << path[i] << " \n"[i == 1];}} else {cout << "-1" << '\n';}
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m >> k;for (int i = 1; i <= m; i++) {cin >> edges[i].x >> edges[i].y >> edges[i].v;}for (int i = 1; i <= k; i++) {int x, y;cin >> x >> y;bellmanFod(x, y);}
}

3.租房

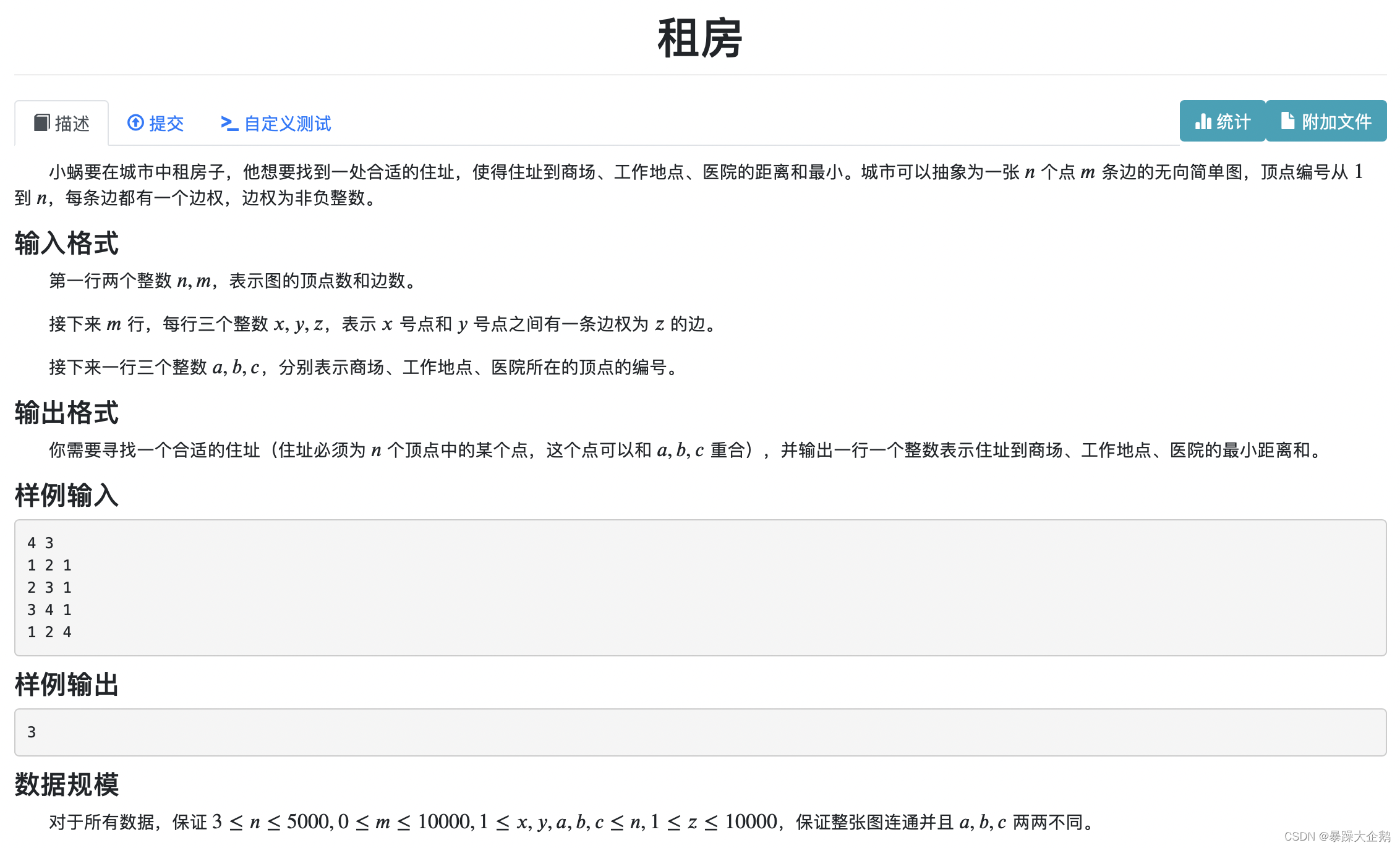
//租房
#include <bits/stdc++.h>
using namespace std;
int n, m, k, a, b, c, cnt;
struct node {int x, y, v;
} edges[20001];
int dis[10001], f[3][10001];inline void bellmanFod(int s) {memset(dis, 127, sizeof(dis));dis[s] = 0;while (1) {bool ok = 0;for (int i = 1; i <= cnt; i++) {int x = edges[i].x, y = edges[i].y, v = edges[i].v;if (dis[x] < 1 << 30) {if (dis[x] + v < dis[y]) {dis[y] = dis[x] + v;ok = 1;}}}if (!ok) {break;}}
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m;cnt = 0;for (int i = 1; i <= m; i++) {int x, y, z;cin >> x >> y >> z;edges[++cnt].x = x, edges[cnt].y = y, edges[cnt].v = z;edges[++cnt].x = y, edges[cnt].y = x, edges[cnt].v = z;}cin >> a >> b >> c;bellmanFod(a);memcpy(f[0], dis, sizeof(dis));bellmanFod(b);memcpy(f[1], dis, sizeof(dis));bellmanFod(c);memcpy(f[2], dis, sizeof(dis));int ans = 1 << 30;for (int i = 1; i <= n; i++) {ans = min(ans, f[0][i] + f[1][i] + f[2][i]);}cout << ans << '\n';
}

4.小蜗的旅行

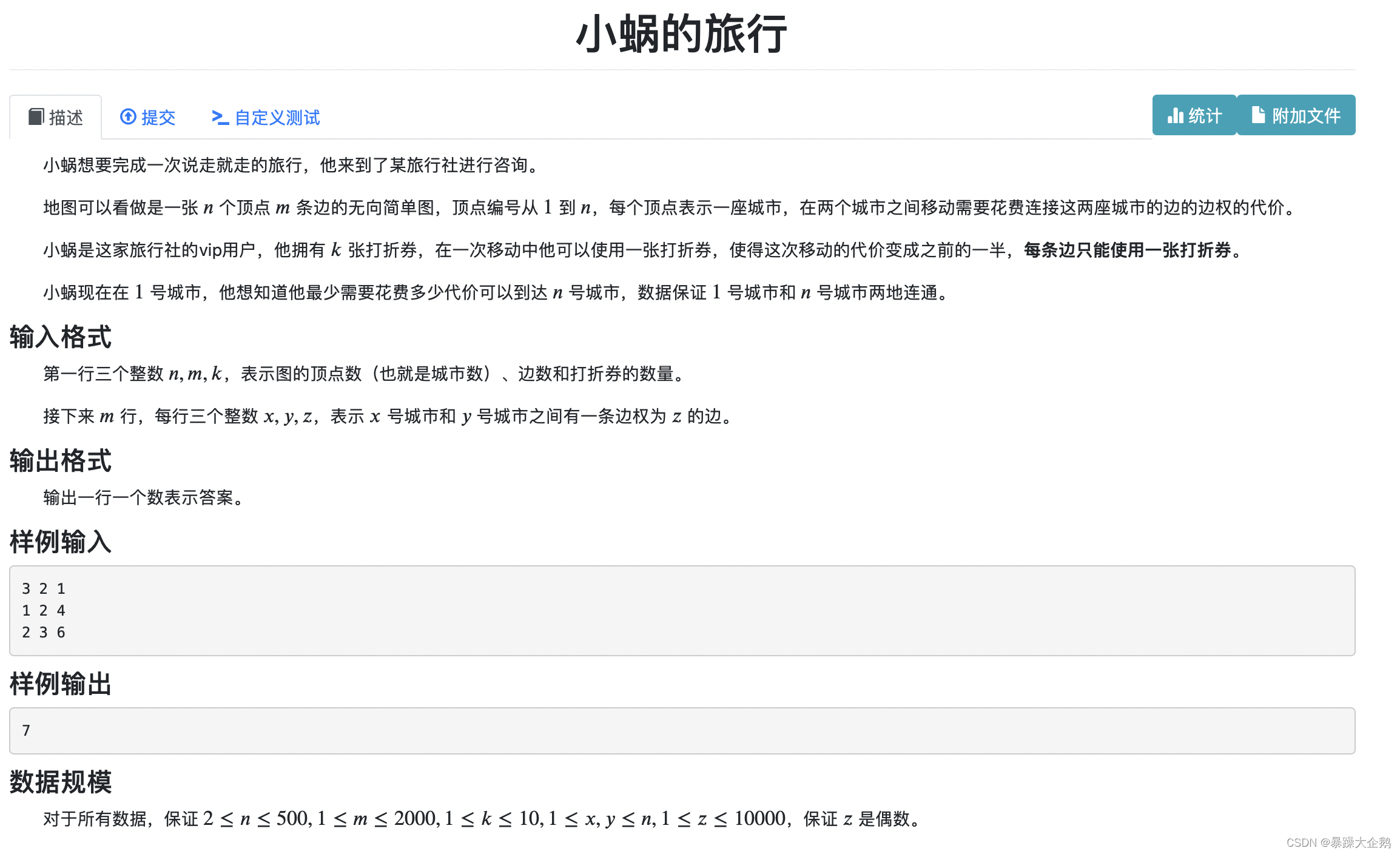
//小蜗的旅行
#include <bits/stdc++.h>
using namespace std;
int n, m, k, cnt;
struct node {int x, y, v;
} edges[20001];
int dis[501][11];inline void bellmanFod(int s, int f) {memset(dis, 127, sizeof(dis));dis[s][0] = 0;for (int i = 1; i <= n; i++) {bool ok = 0;for (int j = 1; j <= cnt; j++) {int x = edges[j].x, y = edges[j].y, v = edges[j].v;for (int l = 0; l <= k; l++) {if (dis[x][l] < 1 << 30) {if (dis[x][l] + v < dis[y][l]) {dis[y][l] = dis[x][l] + v;ok = 1;}if (l != k && dis[x][l] + v / 2 < dis[y][l + 1]) {dis[y][l + 1] = dis[x][l] + v / 2;ok = 1;}}}}if (!ok) {break;}}int ans = 1 << 30;for (int i = 0; i <= k; i++) {ans = min(ans, dis[n][i]);}cout << ans << '\n';
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m >> k;cnt = 0;for (int i = 1; i <= m; i++) {int x, y, z;cin >> x >> y >> z;edges[++cnt].x = x, edges[cnt].y = y, edges[cnt].v = z;edges[++cnt].x = y, edges[cnt].y = x, edges[cnt].v = z;}bellmanFod(1, n);
}