零基础代码随想录【Day42】|| 1049. 最后一块石头的重量 II，494. 目标和，474.一和零

本文主要是介绍零基础代码随想录【Day42】|| 1049. 最后一块石头的重量 II，494. 目标和，474.一和零，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

DAY42

1049.最后一块石头的重量II

解题思路&代码

494.目标和

解题思路&代码

474.一和零

解题思路&代码

---

DAY42

1049.最后一块石头的重量II

力扣题目链接(opens new window)

题目难度：中等

有一堆石头，每块石头的重量都是正整数。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；

如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。

示例：

• 输入：[2,7,4,1,8,1]
• 输出：1

解释：

• 组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
• 组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
• 组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
• 组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

解题思路&代码

思路：

关键点：认识到什么是应用类背包问题，此处如何联系到背包？尽量把容器分成大小相等的两堆，则另一堆是否能用数组元素填满多少则是涉及到了背包最多能装多少的问题

本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了。

是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。

本题物品的重量为stones[i]，物品的价值也为stones[i]。

对应着01背包里的物品重量weight[i]和 物品价值value[i]。

1.确定dp数组以及下标的含义

dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]。

可以回忆一下01背包中，dp[j]的含义，容量为j的背包，最多可以装的价值为 dp[j]。

2.确定递推公式

01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

本题则是：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);

3.dp数组如何初始化

既然 dp[j]中的j表示容量，那么最大容量（重量）是多少呢，就是所有石头的重量和。

因为提示中给出1 <= stones.length <= 30，1 <= stones[i] <= 1000，所以最大重量就是30 * 1000 。

而我们要求的target其实只是最大重量的一半，所以dp数组开到15000大小就可以了

4.确定遍历顺序

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中就已经说明：如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！

• 时间复杂度：O(m × n) , m是石头总重量（准确的说是总重量的一半），n为石头块数
• 空间复杂度：O(m)

class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int i : stones) {sum += i;}int target = sum >> 1;//初始化dp数组int[] dp = new int[target + 1];//为什么要+1，因为涉及到背包重量为0的情况，要初始化，但是实际上数组元素是不包括这个的for (int i = 0; i < stones.length; i++) {//采用倒序for (int j = target; j >= stones[i]; j--) {//两种情况，要么放，要么不放dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}

494.目标和

力扣题目链接(opens new window)

难度：中等

给定一个非负整数数组，a1, a2, ..., an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。

返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例：

• 输入：nums: [1, 1, 1, 1, 1], S: 3
• 输出：5

解释：

• -1+1+1+1+1 = 3
• +1-1+1+1+1 = 3
• +1+1-1+1+1 = 3
• +1+1+1-1+1 = 3
• +1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。

 

解题思路&代码

思路：

本题要如何使表达式结果为target，

既然为target，那么就一定有 left组合 - right组合 = target。

left + right = sum，而sum是固定的。right = sum - left

公式来了， left - (sum - left) = target 推导出 left = (target + sum)/2 。

target是固定的，sum是固定的，left就可以求出来。

此时问题就是在集合nums中找出和为left的组合

再回归到01背包问题，为什么是01背包呢？

因为每个物品（题目中的1）只用一次！

这次和之前遇到的背包问题不一样了，之前都是求容量为j的背包，最多能装多少。

本题则是装满有几种方法。其实这就是一个组合问题了。

1.确定dp数组以及下标的含义

dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

其实也可以使用二维dp数组来求解本题，dp[i][j]：使用 下标为[0, i]的nums[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种方法。

2.确定递推公式

有哪些来源可以推出dp[j]呢？

只要搞到nums[i]，凑成dp[j]就有dp[j - nums[i]] 种方法。

例如：dp[j]，j 为5，

• 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 容量为5的背包。
• 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 容量为5的背包。
• 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 容量为5的背包
• 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 容量为5的背包
• 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。

所以求组合类问题的公式，都是类似这种：

dp[j] += dp[j - nums[i]]

3.dp数组如何初始化

从递推公式可以看出，在初始化的时候dp[0] 一定要初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递推结果将都是0。

如果数组[0] ，target = 0，那么 bagSize = (target + sum) / 2 = 0。 dp[0]也应该是1， 也就是说给数组里的元素 0 前面无论放加法还是减法，都是 1 种方法。

所以本题我们应该初始化 dp[0] 为 1。

4.确定遍历顺序

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中，我们讲过对于01背包问题一维dp的遍历，nums放在外循环，target在内循环，且内循环倒序。

5.举例推导dp数组

输入：nums: [1, 1, 1, 1, 1], S: 3

bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4

dp数组状态变化如下：

• 时间复杂度：O(n × m)，n为正数个数，m为背包容量
• 空间复杂度：O(m)，m为背包容量

class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i = 0; i < nums.length; i++) sum += nums[i];//如果target的绝对值大于sum，那么是没有方案的if (Math.abs(target) > sum) return 0;//如果(target+sum)除以2的余数不为0，也是没有方案的if ((target + sum) % 2 == 1) return 0;int bagSize = (target + sum) / 2;int[] dp = new int[bagSize + 1];dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = bagSize; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[bagSize];}
}

474.一和零

力扣题目链接(opens new window)

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的大小，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

• 输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3

• 输出：4

• 解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

解题思路&代码

思路：

本题并不是多重背包，再来看一下这个图，捋清几种背包的关系

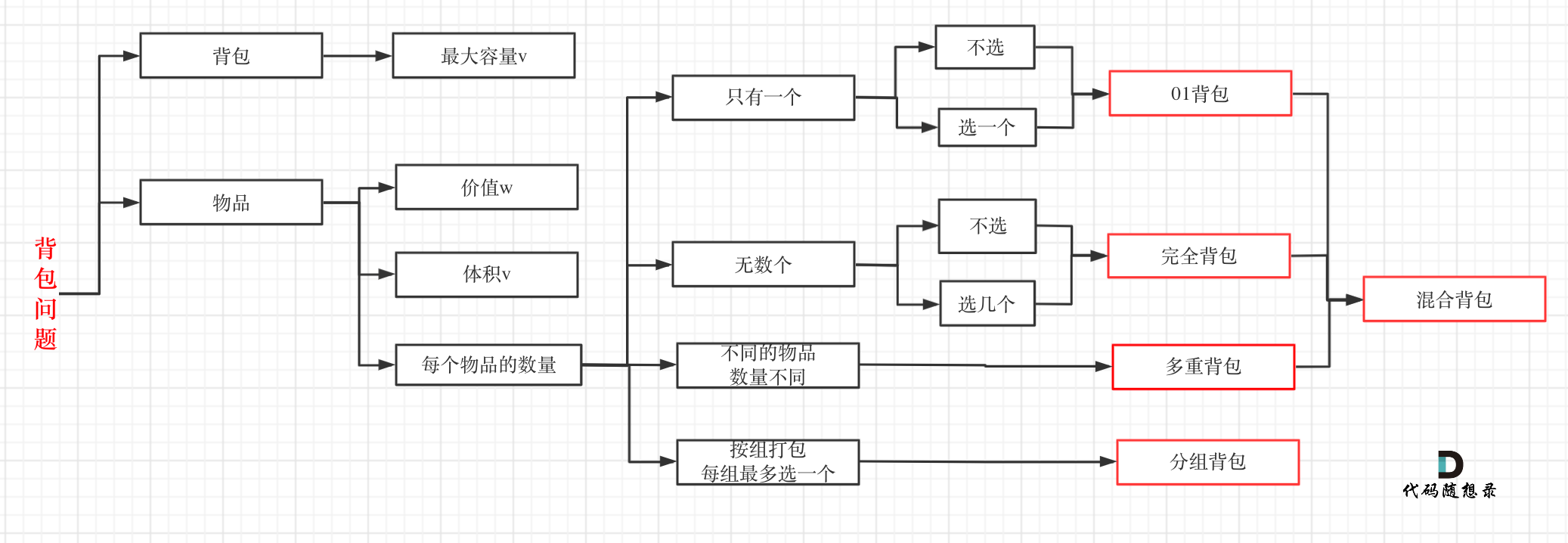
多重背包是每个物品，数量不同的情况。

本题中strs 数组里的元素就是物品，每个物品都是一个！

而m 和 n相当于是一个背包，两个维度的背包。

理解成多重背包的同学主要是把m和n混淆为物品了，感觉这是不同数量的物品，所以以为是多重背包。

但本题其实是01背包问题！

只不过这个背包有两个维度，一个是m 一个是n，而不同长度的字符串就是不同大小的待装物品。

1.确定dp数组（dp table）以及下标的含义

dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

2.确定递推公式

dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。

dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。

然后我们在遍历的过程中，取dp[i][j]的最大值。

所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

此时大家可以回想一下01背包的递推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

对比一下就会发现，字符串的zeroNum和oneNum相当于物品的重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）。

这就是一个典型的01背包！ 只不过物品的重量有了两个维度而已。

3.dp数组如何初始化

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中已经讲解了，01背包的dp数组初始化为0就可以。

因为物品价值不会是负数，初始为0，保证递推的时候dp[i][j]不会被初始值覆盖。

4.确定遍历顺序

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中，我们讲到了01背包为什么一定是外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历！

那么本题也是，物品就是strs里的字符串，背包容量就是题目描述中的m和n。

• 时间复杂度: O(kmn)，k 为strs的长度
• 空间复杂度: O(mn) 

class Solution {public int findMaxForm(String[] strs, int m, int n) {//dp[i][j]表示i个0和j个1时的最大子集int[][] dp = new int[m + 1][n + 1];int oneNum, zeroNum;for (String str : strs) {//正序遍历物品oneNum = 0;zeroNum = 0;for (char ch : str.toCharArray()) {if (ch == '0') {zeroNum++;} else {oneNum++;}}//倒序遍历背包容量for (int i = m; i >= zeroNum; i--) {for (int j = n; j >= oneNum; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
}

这篇关于零基础代码随想录【Day42】|| 1049. 最后一块石头的重量 II，494. 目标和，474.一和零的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---