本文主要是介绍写给妹妹的编程札记 3 - 穷举: 深度优先搜索/广度优先搜索,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前文,我们讨论了从循环遍历到搜索基本框架,并解决了一个经典的八皇后问题。对搜索剪枝也有了一些基本的了解。 下面, 我们来看看搜索的两个最基本的策略: 深度优先搜索和广度优先搜索。
Wikipedia上有比较简单的介绍 (英文版包含更多的参考信息)
深度优先搜索:
http://zh.wikipedia.org/wiki/%E6%B7%B1%E5%BA%A6%E4%BC%98%E5%85%88%E6%90%9C%E7%B4%A2
http://en.wikipedia.org/wiki/Depth-first_search
广度优先搜索:
http://zh.wikipedia.org/wiki/%E5%B9%BF%E5%BA%A6%E4%BC%98%E5%85%88%E6%90%9C%E7%B4%A2
http://en.wikipedia.org/wiki/Breadth-first_search
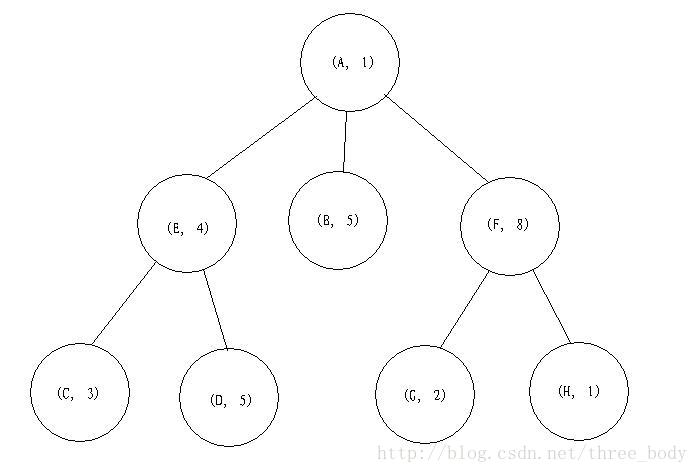
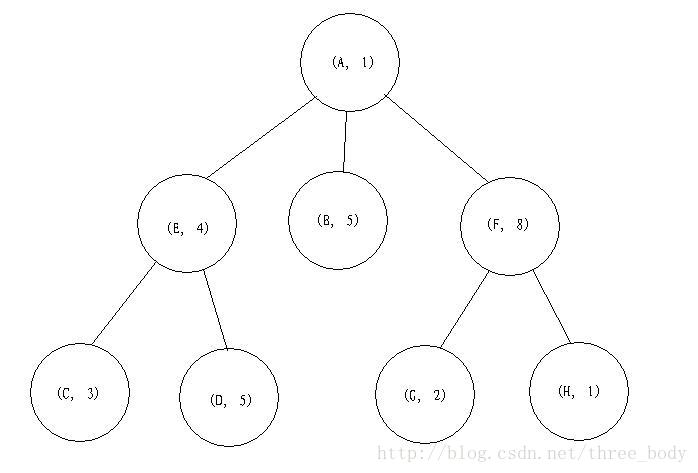
首先看一个比较简单的例子, 假如我们要搜索树数据结构上的节点,找出树结构上权重为5的节点,如果存在多个权重为5的节点,返回距离根节点最近的任意一个。在这里例子中, 之所以说简单的原因在于从根节点出发, 到每个节点只有一条路径可以达到。实际场景中,搜索空间中节点之间关系可能是复杂的,两个节点之间有多条可达路径。
下面首先看深度优先搜索,怎么进行搜索?
第一步:搜索根节点 (A, 1), 权重为1, 并不等于5
第二步:任意挑选一个子节点继续 (深度+1), 访问(E, 4), 权重为4, 并不等于5
第三步:任意挑选一个当前节点的子节点继续 (深度+1) - 访问(C, 3)
这里就是体现了深度优先, 虽然根节点(A, 1)的子节点(B, 5), (F, 8) 还没有遍历, 但我们优先往纵深方向遍历
(C, 3) 的权重为3, 也不等于5
第四步:任意挑选一个当前节点的子节点继续(深度+1) ?
不过,我们发现(C, 3) 没有”更深“的子节点。 怎么办? 这个时候,我们需要回溯, 也就是访问上一个节点的其他子节点。
(C, 3)的上个节点是什么?我们需要保存这个信息,后进先出的栈结构适合这个需求。 因为回溯的时候,最先需要访问的是最后压入栈的节点。
当我们知道(C, 3)的上一个节点是(E, 4)后, 我们在第四步,尝试访问(E, 4)尚未访问过的节点(D, 5)
节点(D, 5)的权重等于5。 我们找到一个候选!
这个时候,我们能够停止了吗? 如果题目要求只要找到任意一个权重等于5的话,我们已经找到了。
但,由于题目要求如果多个节点权重相等,需要返回距离根节点比较近的。 所以我们还需要继续遍历下去......
......
我们尝试结合栈数据结构,重新整理一下上面的搜索过程:
第一步:判断根节点(A, 1), 权重不等于5
把根节点压入栈, 栈中包含元素[ (A, 1)
第二步:任意挑选栈顶元素(A, 1)的“尚未访问过”的一个子节点(E, 4)进行访问
判断节点(E, 4)的权重,权重不等于5
把节点(E, 4)压入栈,栈中包含元素[ (A, 1), (E, 4)
第三步:任意挑选栈顶元素(E, 4)的“尚未访问过”的一个子节点(C, 3)进行访问
判断节点(C, 3)的权重,权重不等于5
把节点(C, 3)压入栈,栈中包含元素[ (A, 1), (E, 4), (C, 3)
第四步:任意挑选栈顶元素(C, 3)的“尚未访问过”的一个子节点进行访问,
但(C, 3)没有子节点, 把节点(C, 3)弹出栈,栈中包含元素[ (A, 1), (E, 4)
第五步:任意挑选栈顶元素(E, 4)的“尚未访问过”的一个子节点(D, 5)进行访问,
判断节点(D, 5)的权重,权重等于5, 记录下一个解
把节点(D, 5)压入栈,栈中包含元素[ (A, 1), (E, 4), (D, 5)
第六步:任意挑选栈顶元素(D, 5)的“尚未访问过”的一个子节点进行访问,
但(D, 5)没有子节点, 把节点(D, 5)弹出栈,栈中包含元素[ (A, 1), (E, 4)
第六步:任意挑选栈顶元素(E, 4)的“尚未访问过”的一个子节点进行访问,
但(E, 4)没有”尚未访问过的“子节点, 把节点(E, 4)弹出栈,栈中包含元素[ (A, 1)
......
一直进行到栈空为止
可以看到上面的每一步操作,已经比较”机械“, 类似于《写给妹妹的编程札记 1 - 穷举: 从循环到递归》的转化,不难写出搜索程序。虽然上面描述的时候, 我们显式定义了栈数据结构,但实际程序中,有时也可以直接利用递归程序本身使用的系统调用栈。
接下来,我们再来看广度优先搜索,怎么进行的?
第一步:搜索根节点 (A, 1), 权重为1, 并不等于5
第二步:遍历根节点的所有子节点
这里就是体现了广度优先,优先遍历当前看到的所有子节点
2.a 访问节点(E, 4), 权重为4, 并不等于5
2.b 访问节点(B, 5), 权重为5, 等于5!
2.c 访问节点(F, 8), 权重为8, 并不等于5
这个时候,我们已经找到一个解,节点(B, 5), 是否应该结束呢?
对于当前问题, 我们可以结束了。 因为不可能还有其他权重等于5的节点,距离根节点比(B, 5)还要近。
如果题目要求我们找到所有权重为5的节点,那么,我们还需要继续,直到遍历完所有节点。
第三步:在遍历完所有根节点的子节点后, 下一步,我们应该是要遍历根节点子节点的子节点。
我们怎么知道根节点的子节点是什么呢? 需要一个额外的数据结构存储起来。
先进先出的队列适合这个要求,因为我们按访问过的子节点顺序,遍历这些子节点的子节点
首先,遍历根节点的第一个子节点(E, 4)的所有子节点:
3.a 访问节点(C, 3), 权重为3, 并不等于5
3.b 访问节点(D, 5), 权重为5, 等于5!又找到一个解。
......
类似地,我们尝试结合队列数据结构,重新整理一下上面的搜索过程:
第一步:访问根节点(A, 1), 权重不等于5
把根节点插入队列, 队列中包含元素 <(A, 1)>
第二步:遍历队首节点(A,1)的所有“尚未访问过”子节点
2.a 访问节点(E, 4), 权重为4, 并不等于5
把节点(E, 4)插入队列, 队列中包含元素<(A, 1), (E, 4)>
到此为止,队首节点(A, 1)的所有子节点已经遍历完,可以把队首元素从队列中删除, 此时队列中包含元素<(E, 4), (B, 5), (F, 8)>
队列数据结构,始终保存着已经被遍历,但子节点尚未被遍历的所有节点的集合。
第三步:遍历队首节点(E,4)的所有“尚未访问过”子节点
......
一直进行到队列为空为止。
深度优先搜索和广度优先搜索的基本思想,如上面描述这样,非常直接和容易理解。简单的比较可以给我们一个印象:
1. 一般如果需要找出所有解, 深度优先搜索会比广度优先搜索好。 虽然两者时间复杂度上差不多,但广度优先搜索需要比较大的空间来存储队列。
2. 求最优解时, 一般可以优先考虑广度优先搜索。深度优先搜索一般需要遍历所有可能,而广度优先可以通过设计使得寻找到的第一个就是最优的。
深度优先搜索和广度优先搜索的取舍还是需要具体问题具体分析。 她们是非常基本的框架,在这些基本框架的基础上, 有很多变种,技巧,技术和演化。如: A*, alpha-beta剪枝, 爬山法,beam search等等等等。 有些巧妙的算法,也充分利用和吸收了这些基本搜索策略。如,有向图的强连通分支可以通过两次深度优先遍历得到, 单源最短路的Dijkstra算法跟广度优先算法类似等等。
这篇关于写给妹妹的编程札记 3 - 穷举: 深度优先搜索/广度优先搜索的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!