本文主要是介绍(毫米波雷达数据处理中的)聚类算法(3) – K-means算法及其实践,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
说明
读者在阅读本文前,建议先看看本系列的前两篇文章:[1]:(毫米波雷达数据处理中的)聚类算法(1) --- 概述-CSDN博客 [2]:(毫米波雷达数据处理中的)聚类算法(2) – DBSCAN算法及其实践-CSDN博客
K-means算法因为需要提前给出簇的数量,(这在车载雷达的实际应用上是不可取的:我们无法确定在行车过程中车辆前方有多少个目标物,相反地,我们是聚类之后才知道有多少个目标物..),正因如此,该算法无法在车载雷达上实践,不过就像在[1]中所说,本系列文章其实也不只针对车载毫米波雷达的数据处理,加之该算法似乎在其它的领域应用还蛮多的(而且相对比较简单、容易实现),所以我在本系列中也加入了该算法。
Blog
2024.5.15 博文第一次撰写
目录
说明
目录
一、K-means算法介绍
二、基于K-means的Iris数据集聚类实践
2.1 关于Iris数据集
2.2 基于K-means算法的处理结果
三、基于K-means的自生成二维平面点簇数据集聚类实践
3.1 二维平面点簇生成结果
3.2 基于K-means算法的处理结果
四、总结
五、参考资料
六、参考代码与数据集
一、K-means算法介绍
K-means聚类算法是一种迭代求解的聚类分析算法。网上有很多的参考资料,比如[3]。 该算法的基本思想是,通过迭代寻找K个簇的一种聚类方案,使得聚类结果对应的损失函数最小。其中,损失函数可以定义为各个样本距离所属簇中心点的误差平方和:
![]() (1-1)
(1-1)
式中,![]() 表示第i个样本,
表示第i个样本,![]() 表示第i个样本所在簇的簇中心点,N是总的样本数。 该算法典型的流程图如下:
表示第i个样本所在簇的簇中心点,N是总的样本数。 该算法典型的流程图如下:
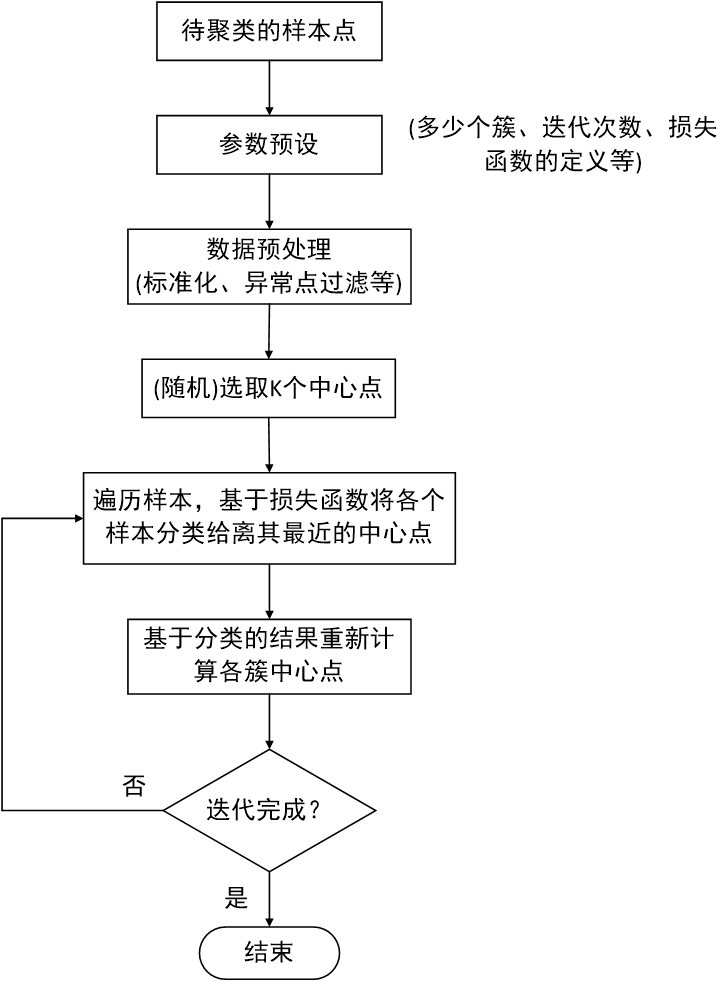
图1.1 典型的K-means算法处理流程图
该算法表现依赖于簇数量的预设以及初始样本中心的选取是否合适。
二、基于K-means的Iris数据集聚类实践
2.1 关于Iris数据集
关于Iris数据集的介绍我已经在文章[2]中有过比较详细的说明,这里不再赘述。Iris数据集经过降维后,结果如下:
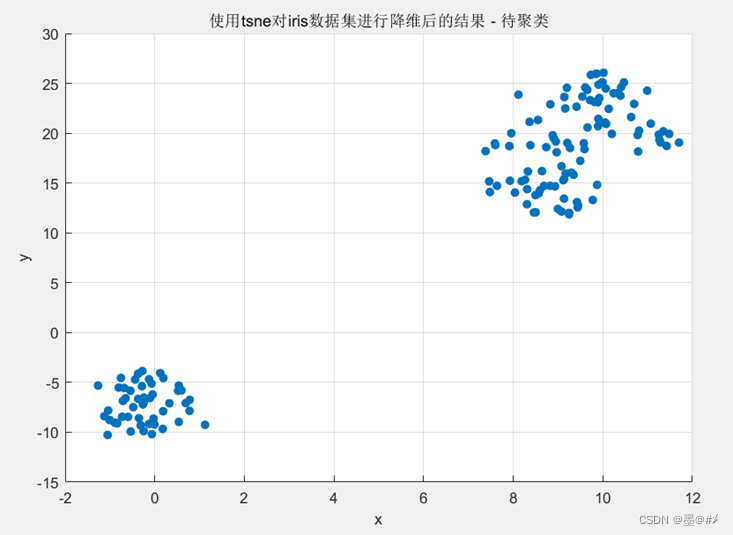
图2.1 对Iris数据集进行降维后的结果
从图中可以看到两个明显分离的点簇,右上角的点簇细看似乎也可以分成两个,Iris数据集给每个点都有一个预设的分类,这里再基于上图画出其原始的分类:
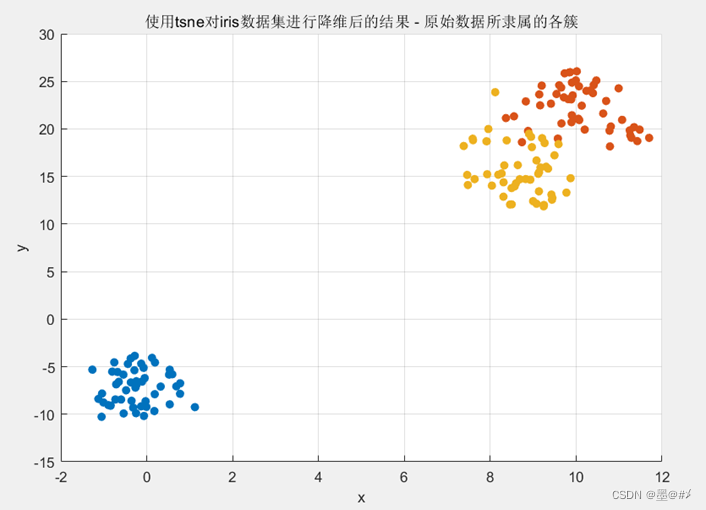
图2.2 降维后的Iris数据集各点所属分类
我们期望使用K-means聚类后可以得到与图2.2相近的效果。
2.2 基于K-means算法的处理结果
本次仿真中,我预设簇的个数为3,迭代20次,以各个样本距离所属簇中心点的误差平方和作为损失函数,初始中心点是随机选取的。得到的结果如下:

图2.3 不同迭代次数下损失值的变化
从图中可以看到,实际上迭代3次后,聚类的结果就已经趋于平稳。聚类的结果如下:
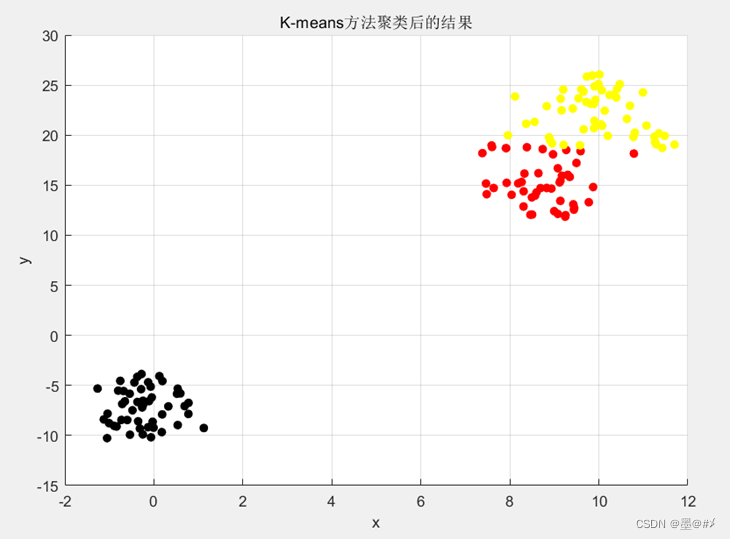
图2.4 K-means算法聚类结果
对比图2.2,聚类的效果是符合预期的。计算该聚类结果的各评价指标得到:

图2.5 K-means聚类结果的客观评价指标计算结果
【为方便与DBSCAN算法比较,我在代码中对两聚类算法使用的是同一组数据】
读者可以结合博文[2]的结果、以及博文[1]中对这几个客观评价指标的描述做一些更深入的对比和分析。
三、基于K-means的自生成二维平面点簇数据集聚类实践
3.1 二维平面点簇生成结果
关于二维平面点簇的介绍我在博文[1]中已经有过说明,这里不再赘述。和[1]中同样的参数设计下,生成的点簇如下图所示:

图3.1 随机生成的待聚类点簇
原始点的各所属分类如下:
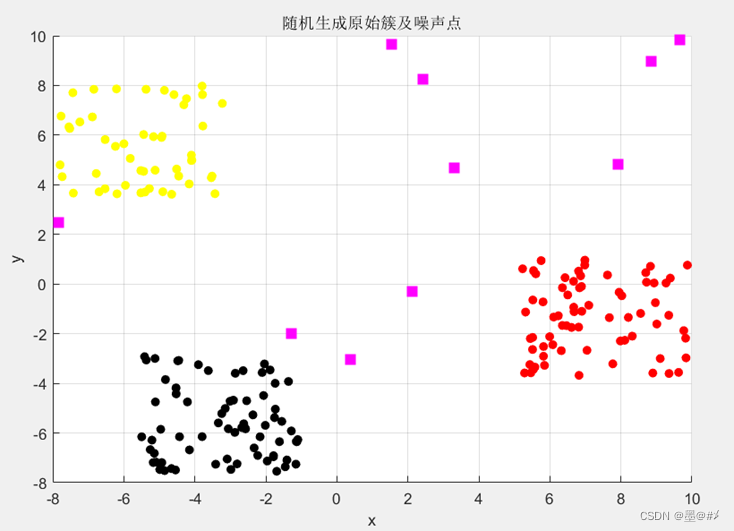
图3.2 随机生成的点簇各点的所属分类示意图
图中,三种不同颜色的圆点对应三个簇,品红色的矩形方块对应噪声点。在后续的聚类实践中,我们期望聚类的结果应尽可能符合本图。
3.2 基于K-means算法的处理结果
仿真中,预设簇的个数为3,迭代20次,以各个样本距离所属簇中心点的误差平方和作为损失函数,初始中心点是随机选取的。得到的结果如下:
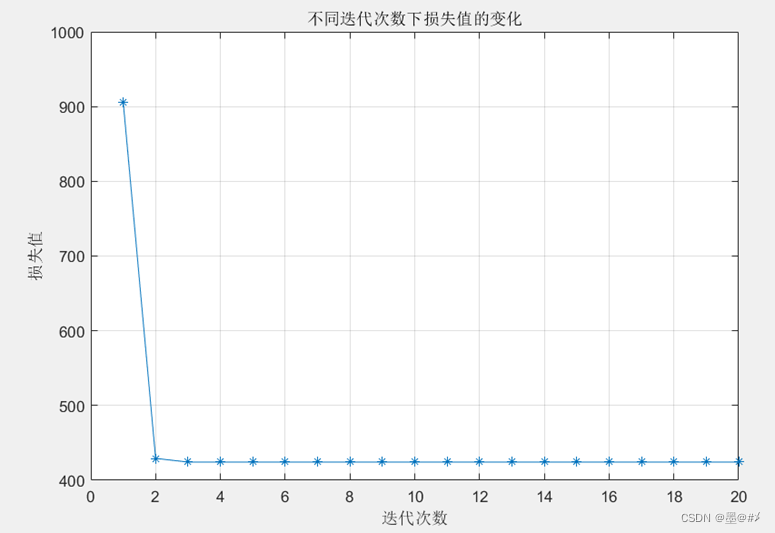
图3.3 不同迭代次数下损失值的变化
可以看到,迭代到第3次时聚类的结果就已经趋于平稳。聚类的结果如下:
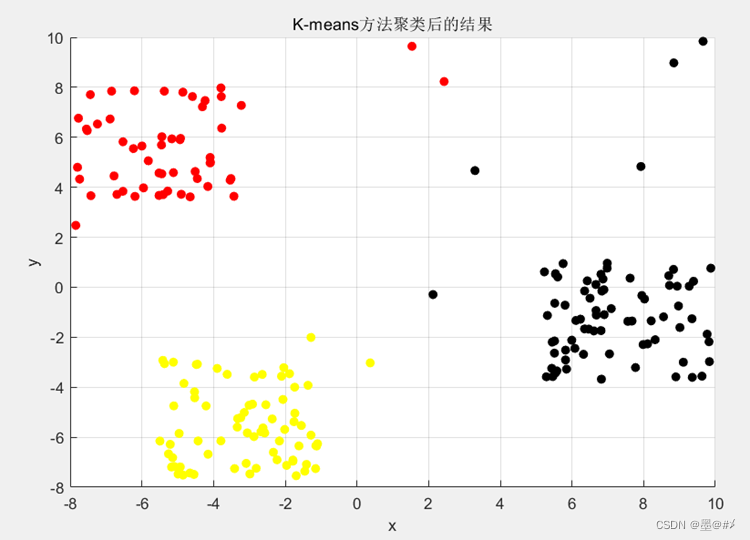
图3.4 K-means聚类结果
结果符合预期,不过K-means相较于[2]中的DBSCAN算法,K-means无法“筛选出”噪点,所以在图1.1对于该算法的处理流程介绍中,有一个数据预处理(清除异常点)的操作,不过在本文的两次实践中我都没有做。
前述聚类结果下的客观评价指标的值计算如下:

图3.5 K-means聚类结果的客观评价指标计算结果
【为方便与DBSCAN算法比较,我在代码中对两聚类算法使用的是同一组数据】
读者可以结合博文[2]的结果、以及博文[1]中对这几个客观评价指标的描述做一些更深入的对比和分析。
在第一章对该算的介绍中就提到:该算法表现依赖于簇数量的预设以及初始样本中心的选取是否合适。虽然本章的仿真下初始点是随机选取的,且聚类的结果也达到了预期的效果,但如果多次试验,是会遇到类似下图这种情况的(有两个初始点落在了同一个簇里面):
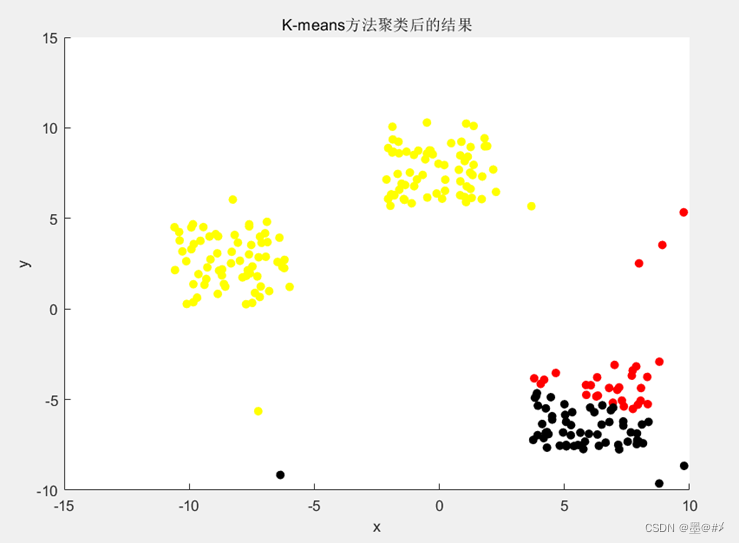
图3.6 初始点选取不合适导致聚类效果差
读者可以基于后文提供的代码自行尝试和理解。
四、总结
本文对K-means算法进行了实践。首先对K-means算法进行了简单的介绍,并给出了其典型的算法流程图。随后分别给出了基于K-means算法对Iris数据集、自己生成的二维平面点簇形数据集的聚类结果。
五、参考资料
[1] (毫米波雷达数据处理中的)聚类算法(1) --- 概述-CSDN博客
[2] (毫米波雷达数据处理中的)聚类算法(2) – DBSCAN算法及其实践-CSDN博客
[3] KMeans聚类算法详解 - 知乎 (zhihu.com)
六、参考代码与数据集
我将本聚类算法系列的三篇博文所涉及的代码和数据集打包成了一份,其内含如下内容:
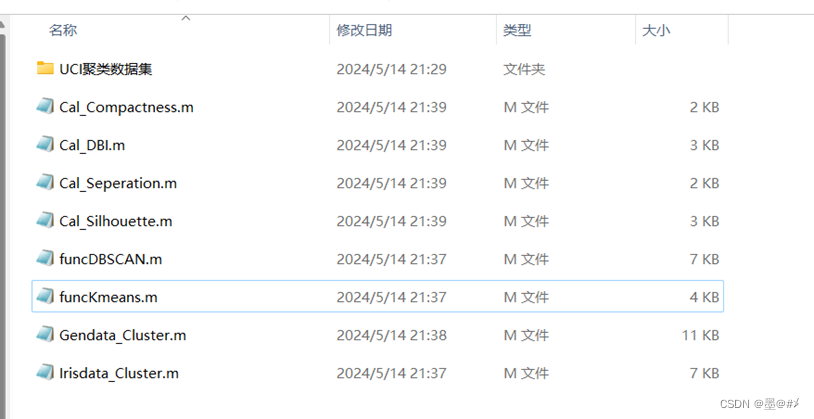
图中,UCI聚类数据集包含了多个可用于聚类算法实践的数据集;前四个m文件为[1]中第4章所介绍的四种客观评价指标的计算函数;funcDBSCAN为基于DBSCAN算法的聚类函数,funcKmeans为基于K-means算法的聚类函数;Gendata_Cluster.m为主函数,该函数首先生成点簇数据集,然后分别调用funcDBSCAN.m、funcKmeans.m完成聚类以及聚类结果的展示,最后再分别调用前面的四个客观指标计算函数完成客观评价指标的计算;Irisdata_Cluster.m则是另一个主函数,该函数获取UCI的Iris数据集,并对该数据集做一些处理(包括降维),随后和Gendata_Cluster.m函数一样,完成聚类、客观指标计算等流程。读者可以自行下载参考,链接为(抱歉,要收费):
(毫米波雷达数据处理中的)聚类算法系列博文对应的代码和数据集资源-CSDN文库
这篇关于(毫米波雷达数据处理中的)聚类算法(3) – K-means算法及其实践的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!

