本文主要是介绍《机器学习实战》笔记之十二——使用FP-Growth算法来高效发现频繁项集,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
第十二章 使用FP-Growth算法来高效发现频繁项集
FP-growth算法,基于Apriori构建,但在完成相同任务时采用了不同的技术,其只需要对数据库进行两次扫描,而Apriori算法对于每个潜在的频繁项集都会扫描数据集判定给定模式是否频繁,因此其比Apriori算法快。FP算法需要将数据集存储在一个特定的称作FP树的结构之后发现频繁项集或者频繁项对。
12.1 FP树:用于编码数据集的有效方式
FP-growth算法将数据存储在一种称为FP树的紧凑数据结构中。FP(Frequent Pattern)通过链接来连接相似元素,被连起来的元素项可以看成一个链表。
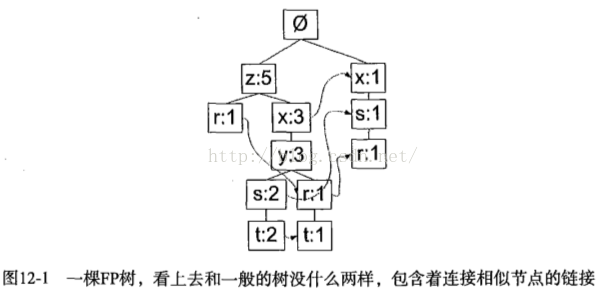
同搜索树不同的是,一个元素项可以在一棵FP树中出现多次。FP树会存储项集的出现频率,而每个项集会以路径的方式存储在树中。存在相似元素的集合会共享树的一部分。只有当集合之间完全不同时,树才会分叉。树节点上给出集合中的单个元素及其在序列中的出现次数,路径会给出该序列的出现次数。相似项之间的链接即节点链接,用于快速发现相似项的位置。
FP-growth算法首先构建FP树,然后利用它来挖掘频繁项集。为构建FP树,需要对原始数据集扫描两遍。第一遍对所有元素项的出现次数进行计数。第二遍扫描只考虑那些频繁元素。
12.2 构建FP树
数据结构:
FP树比其他树更加复杂,因此需要一个类来保存树的每一个节点。
#!/usr/bin/env python # coding=utf-8 class treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = None #用于链接相似的元素项self.parent = parentNode #指向父节点的指针self.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1): #将树以文本形式显示print " "*ind, self.name, " ",self.countfor child in self.children.values():child.disp(ind+1)rootNode = treeNode("pyramid", 9, None) rootNode.children["eye"] = treeNode("eye",13, None) rootNode.disp()rootNode.children["phoenix"] = treeNode("phoenix", 3, None) rootNode.disp()
构建FP树
除了FP树的类,还需要头指针表来指向给定类型的第一个实例。通过头指针表可以快速访问FP树中一个给定类型的所有元素。可用字典保存,并且其value存放FP树中每类元素的总数。
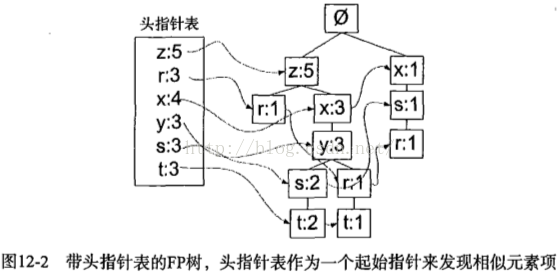
第一遍遍历数据集得到每个元素项的出现频率。去掉不满足最小支持度的元素项。再构建FP树。构建时,读入每个项集并将其添加到一条已经存在的路径中。如果该路径不存在,则创建一条新路径。每个事务就是一个无序集合。假设集合{z,x,y}和{y,z,r},那么在FP树中,相同项只会表示一次。为此在将集合添加到树之前,先对每个集合进行排序,排序基于元素项出现的频率。

在对事务记录过滤和排序之后,就可以构建FP树了。从空集,向其中不断添加频繁项集。过滤、排序后的事务依次添加到树中,如果树中巳存在现有元素,则增加现有元素的值;如果现有元素不存在,则向树添加一个分枝。
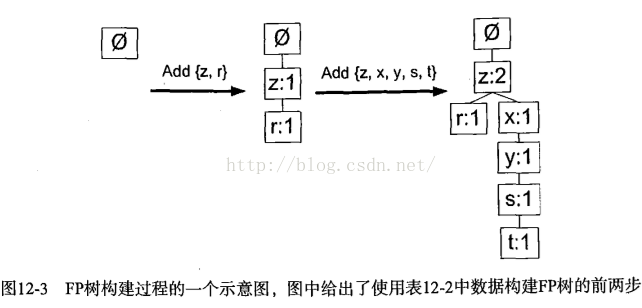
coding:
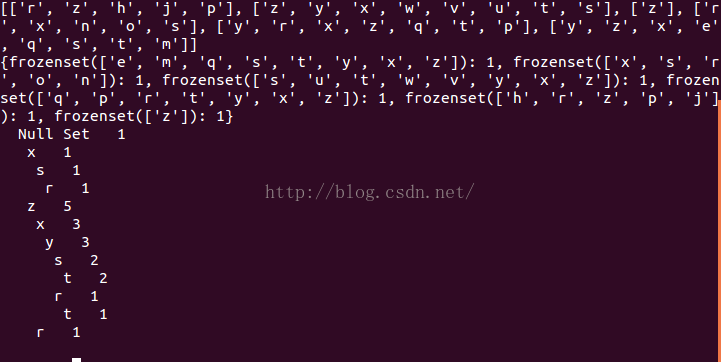
#================FP树构建函数============================= def createTree(dataSet, minSup=1):headerTable = {}for trans in dataSet: #遍历一遍扫描数据集并统计每个元素项出现的频度for item in trans:headerTable[item] = headerTable.get(item,0)+dataSet[trans]for k in headerTable.keys():if headerTable[k] < minSup: #移除不满足最小支持度的元素项del(headerTable[k])freqItemSet = set(headerTable.keys())if len(freqItemSet) == 0: #没有元素退出return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None] #扩展头指针表,第一个元素保存计数,第二个元素指向第一个元素项retTree = treeNode("Null Set", 1, None)for tranSet, count in dataSet.items(): #第二遍,遍历数据集,对每条记录进行处理localD = {}for item in tranSet: #对每条记录中的各个子项赋予其支持度,用于排序if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:orderedItems = [v[0] for v in sorted(localD.items(),key = lambda e:e[1], reverse =True)]updateTree(orderedItems, retTree, headerTable, count) #排序后,对树进行填充return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: #测试第一个元素项是否作为子节点存在inTree.children[items[0]].inc(count)else:inTree.children[items[0]] = treeNode(items[0], count, inTree) #创建树的新节点if headerTable[items[0]][1] == None:headerTable[items[0]][1] = inTree.children[items[0]] #树上的新的节点的值更新else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]]) #如果节点已经有了,这两个进行链接下if len(items) > 1:updateTree(items[1::], inTree.children[items[0]], headerTable, count) #添加了首节点,递归添加剩下的节点def updateHeader(nodeToTest, targetNode):while (nodeToTest.nodeLink !=None):nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNode#========简单数据集及数据包装器================================ def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:retDict[frozenset(trans)] = 1return retDictsimpDat = loadSimpDat() print simpDatinitSet = createInitSet(simpDat) print initSetmyFPtree, myHeaderTab = createTree(initSet, 3) myFPtree.disp()
效果
12.3 从一颗FP树中挖掘频繁项集
有了FP树之后,就可以抽取频繁项集了,首先从单元素项集开始,然后在此基础上逐步构建更大的集合。
步骤:
抽取条件模式基
- 从FP树中获得条件模式基;
- 利用条件模式基,构建一个条件FP树;
- 迭代重复步骤1,2,直到树包含一个元素项为止。
条件模式基是以所查找元素项为结尾的路径集合。每一条路径其实都是一条前缀路径。图12-2中,符号r的前缀路径有{x,s},{z,x,y}和{z}。根据头指针表通过上溯树直到根节点抽取出条件模式基。

创建条件FP树
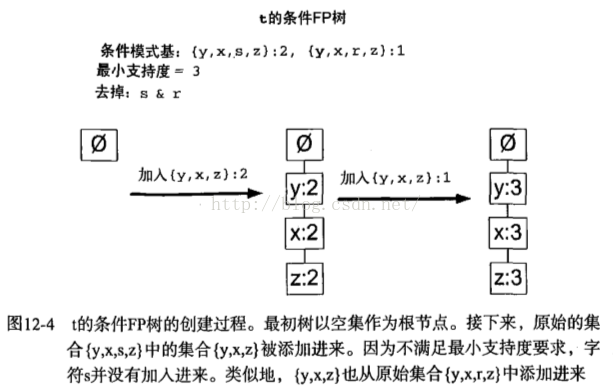
对于每一个频繁项,都要创建一颗条件FP树。通过递归可发现频繁项、条件模式基以及另外的条件树。假设以频繁项t创建一个条件FP树,然后对{t,y}、{t,x}、...等重复该过程。
coding:
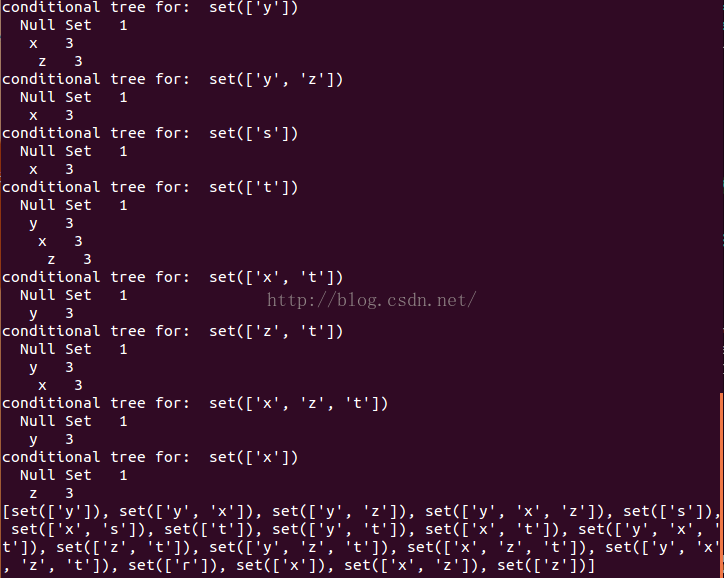
#=========发现以给定元素项结尾的所有路径的函数================= def ascendTree(leafNode, prefixPath):if leafNode.parent !=None: #迭代上溯整颗树prefixPath.append(leafNode.name)ascendTree(leafNode.parent, prefixPath)def findPrefixPath(basePat, treeNode):condPats = {}while treeNode != None:prefixPath = []ascendTree(treeNode, prefixPath)if len(prefixPath) > 1:condPats[frozenset(prefixPath[1:])] = treeNode.counttreeNode = treeNode.nodeLinkreturn condPats #===============递归查找频繁项集的mineTree函数================= def mineTree(inTree, headerTable, minSup, preFix, freqItemList):bigL = [v[0] for v in sorted(headerTable.items(), key=lambda e:e[1])] #从头指针表的底端开始for basePat in bigL: #bigL为头指针,basePat为“t”,"r"等等newFreqSet = preFix.copy()newFreqSet.add(basePat)freqItemList.append(newFreqSet)condPattBases = findPrefixPath(basePat, headerTable[basePat][1]) #创建“t”的条件模式基myCondTree, myHead = createTree(condPattBases, minSup) #以条件模式基构建条件FP树,得到的结果用于下一次迭代if myHead != None: #myHead由createTree函数得到,本质是头指针表变量。print "conditional tree for: ", newFreqSetmyCondTree.disp(1)mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)freqItems = [] mineTree(myFPtree, myHeaderTab, 3, set([]), freqItems) print freqItems
效果:
12.4 示例:从新闻网站点击流中挖掘
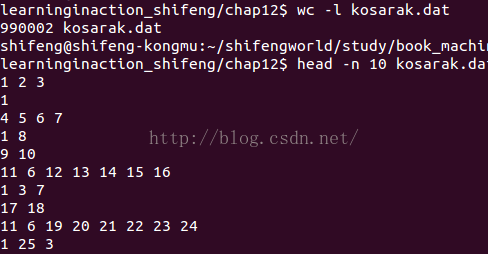
数据:
该文件中的每一行包含某个用户浏览过的新闻报道。一些用户只看过一篇报道,而有些用户看过2498篇报道。用户和报道被编码成整数。
coding:
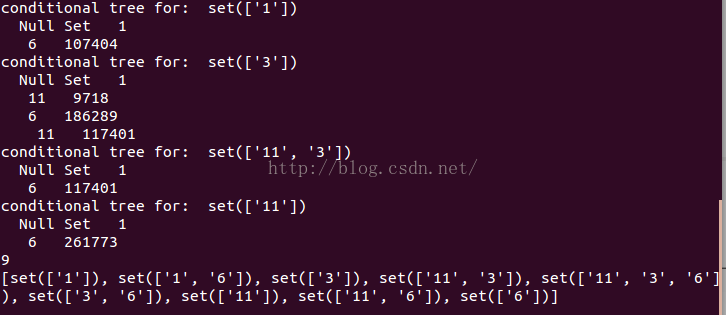
#========================从新闻网站点击流中挖掘================ parsedDat = [line.split() for line in open("kosarak.dat").readlines()] initSet = createInitSet(parsedDat) myFPtree, myHeaderTab = createTree(initSet, 100000) myFreqList = [] mineTree(myFPtree, myHeaderTab, 100000, set([]), myFreqList) print len(myFreqList) print myFreqList
效果:
12.5 小结
FP-growth算法是一种用于发现数据集中频繁模式的有效方法,利用Apriori原理,只对数据集扫描两次,运行更快。在算法中,数据集存储在FP树中,构建完树后,通过查找元素项的条件基及构建条件FP树来发现频繁项集。重复进行直到FP树只包含一个元素为止。
可以使用FP算法在多种文本中查找频繁单词。
这篇关于《机器学习实战》笔记之十二——使用FP-Growth算法来高效发现频繁项集的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






