本文主要是介绍变分自编码器(Variational Autoencoder, VAE),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
why VAE:
关于变分自编码器,这篇文章讲的不错
1. 自编码器(Autoencoder)的基础
2. 引入概率图模型
3. 重参数化技巧
4. 损失函数
5. 应用
变分自编码器(Variational Autoencoder, VAE)
why VAE:
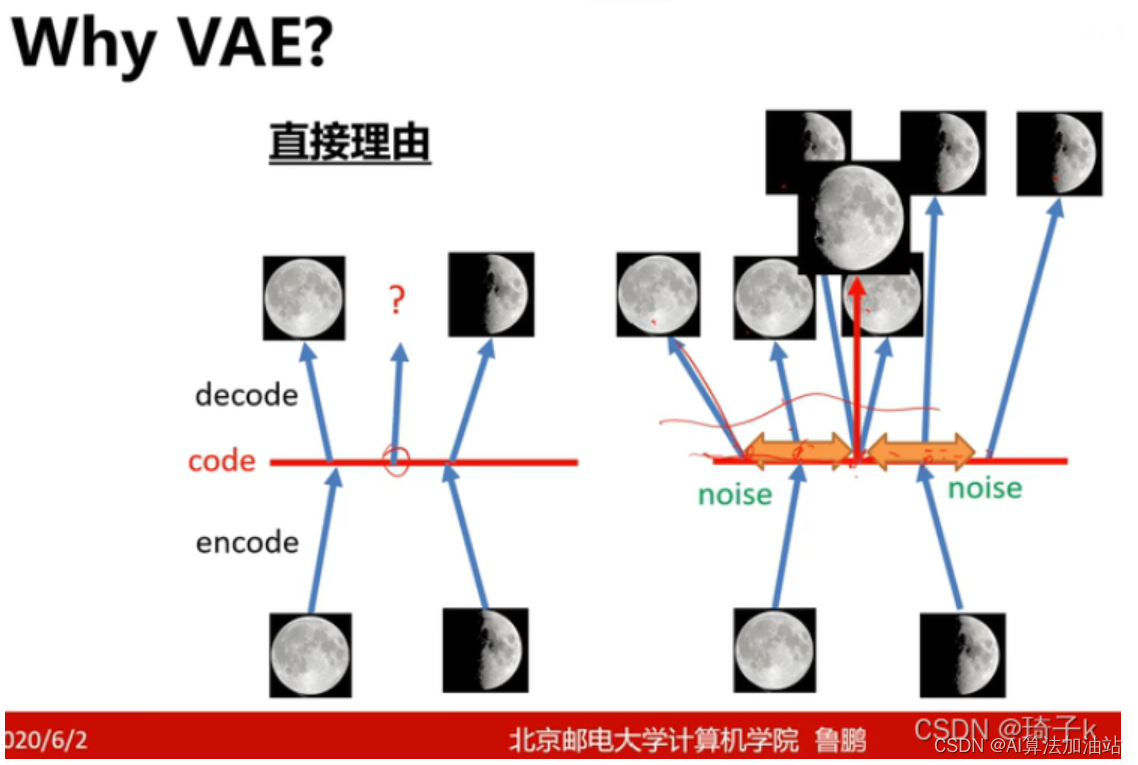
关于变分自编码器,这篇文章讲的不错
机器学习方法—优雅的模型(一):变分自编码器(VAE) - 知乎
变分自编码器(Variational Autoencoder,简称VAE)是一种生成模型,它通过结合深度学习与概率图模型的理念,能够学习输入数据的潜在表示。VAE不仅能够进行数据的压缩编码,还能够生成与训练数据相似的新数据。以下是一些关键点,帮助更好地理解变分自编码器:
1. 自编码器(Autoencoder)的基础
变分自编码器是自编码器的一种扩展。传统的自编码器包括两部分:编码器和解码器。编码器负责将高维输入数据压缩到一个低维潜在空间(latent space),而解码器则负责将这个低维表示恢复成原始数据。自编码器主要用于数据降维和特征学习。
2. 引入概率图模型
变分自编码器与传统自编码器的主要区别在于它引入了概率图模型的概念。在VAE中,编码器不直接输出一个潜在空间的点,而是输出该点的参数,通常是均值和方差。这些参数描述了一个概率分布,通常假设为高斯分布。这意味着每个输入数据点都被映射到一个概率分布上,而不是被映射到一个固定的点上。
3. 重参数化技巧
由于潜在变量是随机的,直接从概率分布中采样会导致无法通过反向传播进行有效的梯度计算。VAE使用一种称为“重参数化技巧”的方法来解决这个问题。具体来说,如果潜在变量 z 服从均值为 μ、方差为 2σ2 的正态分布,那么可以从标准正态分布采样 ϵ,然后计算z=μ+σϵ。这样,随机性仅存在于 ϵ 中,而 μ 和 σ 都是确定的函数,可以通过反向传播来更新。
4. 损失函数
VAE的损失函数包含两部分:一部分是重构误差,即原始数据和通过VAE生成的数据之间的差异;另一部分是KL散度(Kullback-Leibler divergence),它衡量编码后的潜在分布与先验分布(通常是标准正态分布)之间的差异。这种设计既鼓励模型准确重构数据,又使潜在空间的分布有良好的数学性质(例如,使潜在空间连续且无空隙)。
5. 应用
变分自编码器广泛应用于图像生成、半监督学习、异常检测等领域。它们在生成类似于训练数据的新数据方面特别有用。
总的来说,变分自编码器是一种强大的生成模型,它结合了深度学习的表征能力和概率模型的数学框架,使其能够有效地学习复杂数据的生成规律。
这篇关于变分自编码器(Variational Autoencoder, VAE)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








