Local Texture Estimator for Implicit Representation Function

本文主要是介绍Local Texture Estimator for Implicit Representation Function，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

• CVPR2022
• https://github.com/jaewon-lee-b/lte

1. 问题引入

• 现在的任意超分辨率方法使用MLP模型，无法很好的生成高频信息，所以本文提出了一个模型来增加高频信息生成能力，也就是增加超分的细节信息，对应的问题是spectral bias problem；
• 类似于NeRF输入不是直接坐标，而是进行了映射，本文将坐标输入之前也进行了映射；

2. 方法：

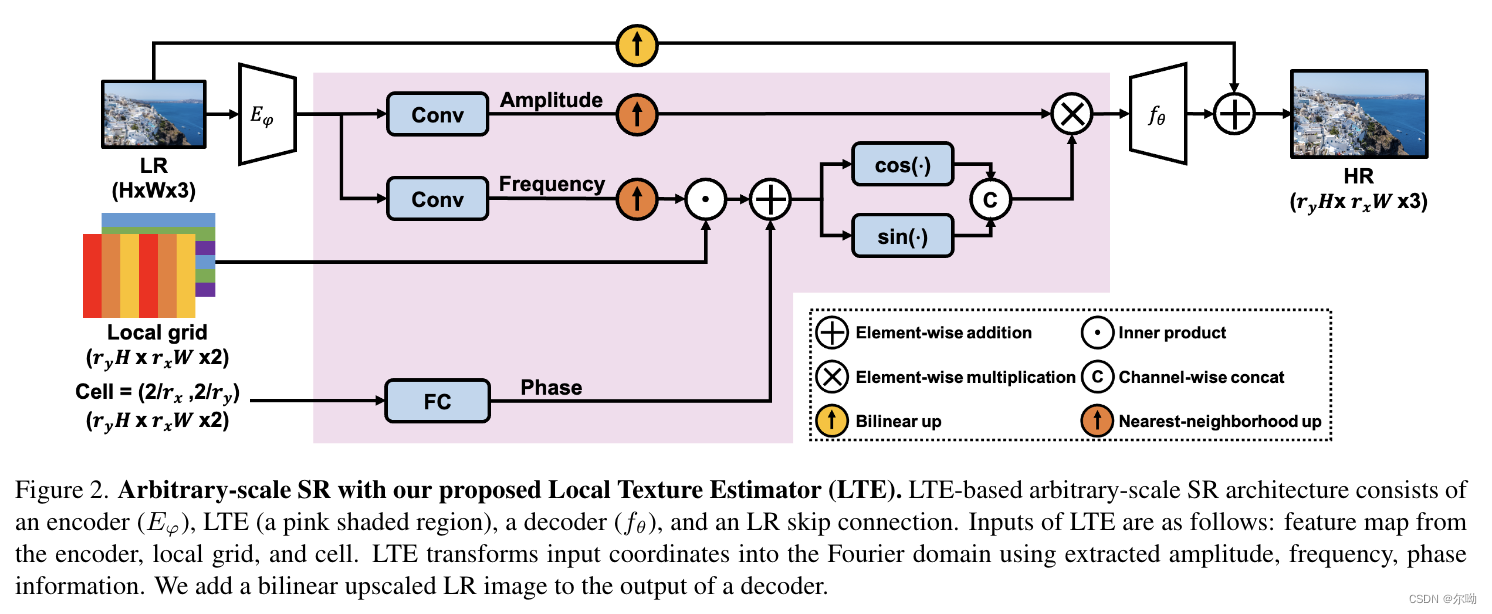
• 整体概览：包含encoder和本文提出的LTE，LTE输出主频率和对应的傅里叶系数，之后一个MLP利用这些输出来重建任意尺寸的HR，低频信息通过一个跳跃连接加入；
  
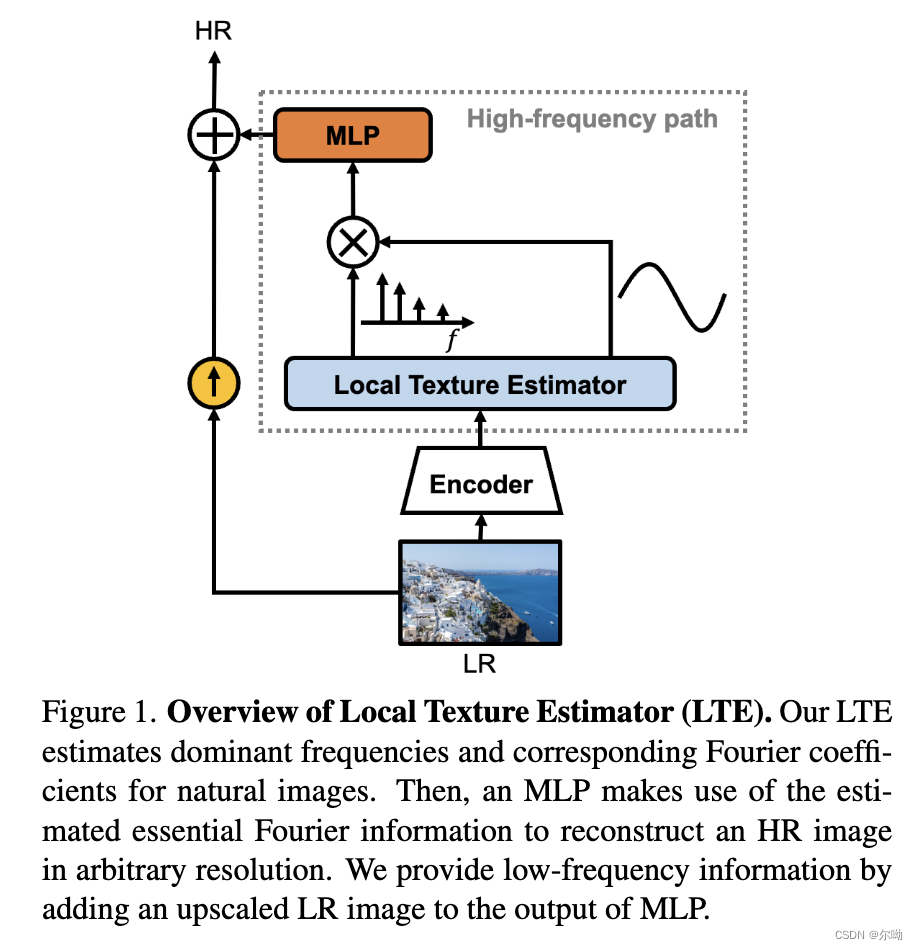
• SR网络：$I^{LR}\in {\mathbb{R}}^{H\times W\times 3}\to I^{HR}\in {\mathbb{R}}^{r_{y}H\times r_{x}W\times 3}$，之前的任意分辨率超分网络例如LIIF公式$s(x,I^{LR};\Theta )={\sum }_{j\in J}{w}_j{f}_{\theta }(z_j,x-x_j)$其中$z=E_{\psi }(I^{LR})$表示latent vector，输入坐标和latent code输出像素值，最后结果是四个方向插值的结果，本文定义local grid是上式中的$x-x_j$；
• 本文为了解决spectral bias problem问题，提出LTE网络，将输入坐标在输入MLP之前先映射到傅里叶域，对应的公式$s(x,I^{LR};\Theta ,\psi )={\sum }_{j\in J}{w}_j{f}_{\theta }(h_{\psi }(z_j,x-x_j))$
• LTE包含三个部分，amplitude estimator $h_a(\cdot ):{\mathbb{R}}^C\to {\mathbb{R}}^{2K}$，frequency estimator $h_f(\cdot ):{\mathbb{R}}^C\to {\mathbb{R}}^{K\times 2}$，phase estimator $h_p(\cdot ):{\mathbb{R}}^2\to {\mathbb{R}}^K$，现有$\delta (=x-x_j)\in {\mathbb{R}}^2$，$h_{\psi }(\cdot ,\cdot ):({\mathbb{R}}^C,{\mathbb{R}}^2)\to {\mathbb{R}}^{2K}$，计算如下，其中$\odot$表示的是按元素相乘，得到的结果是estimated frequencies and corresponding Fourier coefficients
  
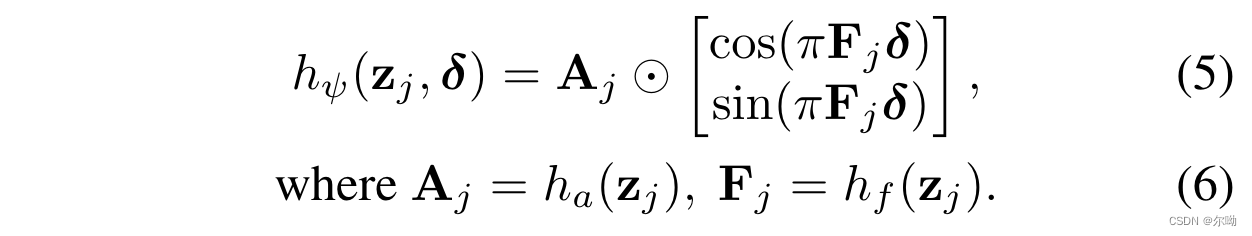
• 还加入了scale进公式，$c$表示cell的尺寸，$\hat{c}=max(c,c_{tr})$，$c_{tr}$是最小cell尺寸：
  
  

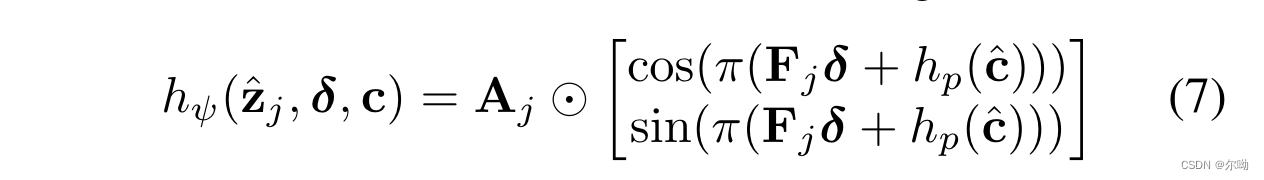
这篇关于Local Texture Estimator for Implicit Representation Function的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---