本文主要是介绍【智能算法】人工原生动物优化算法(APO)原理及实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
- 5.获取代码
1.背景
2024年,X Wang受到自然界原生动物启发,提出了人工原生动物优化算法( Artificial Protozoa Optimizer, APO)。


2.算法原理
2.1算法思想
APO通过模拟原生动物的觅食、休眠和繁殖行为来模拟原生动物的生存机制。

2.2算法过程
觅食行为
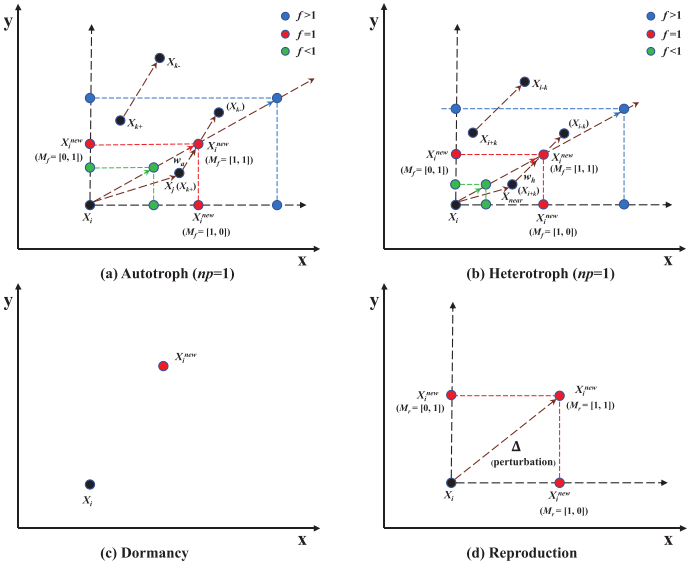
对于觅食行为,作者考虑了原生动物的内部和外部因素。内部因素被认为是原生动物的觅食特征,而外部因素被认为是环境影响,如物种碰撞和竞争行为。
X i n e w = X i + f ⋅ ( X j − X i + 1 n p ⋅ ∑ k = 1 n p w a ⋅ ( X k − − X k + ) ) ⊙ M f X i = [ x i 1 , x i 2 , … , x i d i m ] , X i = s o r t ( X i ) (1) \begin{aligned}&X_{i}^{new}=X_{i}+f\cdot(X_{j}-X_{i}+\frac{1}{np}\cdot\sum_{k=1}^{np}w_{a}\cdot(X_{k-}-X_{k+}))\odot M_{f}\\&X_{i}=[x_{i}^{1},x_{i}^{2},\ldots,x_{i}^{dim}],\quad X_{i}=sort(X_{i})\end{aligned}\tag{1} Xinew=Xi+f⋅(Xj−Xi+np1⋅k=1∑npwa⋅(Xk−−Xk+))⊙MfXi=[xi1,xi2,…,xidim],Xi=sort(Xi)(1)
f = r a n d ⋅ ( 1 + cos ( i t e r i t e r m a x ⋅ π ) ) n p m a x = ⌊ p s − 1 2 ⌋ w a = e − ∣ f ( X k − ) f ( X k + ) + e p s ∣ M f [ d i ] = { 1 , if d i is in r a n d p e r m ( d i m , ⌈ d i m ⋅ i p s ⌉ ) 0 , otherwise (2) f=rand\cdot(1+\cos(\frac{iter}{iter_{max}}\cdot\pi))\\ np_{max}=\lfloor\frac{ps-1}{2}\rfloor \\ w_{a}=e^{-\left|\frac{f(X_{k-})}{f(X_{k+})+eps}\right|}\\ M_f[di]=\begin{cases}1,&\text{if}di\text{is in}\:randperm(dim,\lceil dim\cdot\frac{i}\\{ps}\rceil)\\0,&\text{otherwise}\end{cases}\tag{2} f=rand⋅(1+cos(itermaxiter⋅π))npmax=⌊2ps−1⌋wa=e− f(Xk+)+epsf(Xk−) Mf[di]={1,0,ifdiis inrandperm(dim,⌈dim⋅ips⌉)otherwise(2)
其中𝑋𝑛𝑒𝑤和𝑋分别表示𝑖th原生动物的更新位置和原始位置。𝑋𝑗是随机选择的𝑗th原生动物。𝑋𝑘−表示在𝑘th配对邻居中随机选择一个排序指数小于0.05的原生动物。𝑓表示觅食因子,𝑛𝑝表示外部因素之间的邻居对个数,𝑛𝑝𝑚𝑎为𝑛𝑝的最大值。𝑤𝑎是自养模式下的权重因子,⊙表示Hadamard积。
异养模式在黑暗中,原生动物可以通过从周围环境中吸收有机物来获取营养。假设𝑋𝑛𝑒𝑎𝑟是附近一个食物丰富的地方,原生动物就会向那里移动。
X i n e w = X i + f ⋅ ( X n e a r − X i + 1 n p ⋅ ∑ k = 1 n p w h ⋅ ( X i − k − X i + k ) ) ⊙ M f X n e a r = ( 1 ± R a n d ⋅ ( 1 − i t e r i t e r m a x ) ) ⊙ X i w h = e − ∣ f ( X i − k ) f ( X i + k ) + e p s ∣ R a n d = [ r a n d 1 , r a n d 2 , … , r a n d d i m ] (3) \begin{aligned} &X_{i}^{new}=X_{i}+f\cdot(X_{near}-X_{i}+\frac{1}{np}\cdot\sum_{k=1}^{np}w_{h}\cdot(X_{i-k}-X_{i+k}))\odot M_{f} \\ &X_{near}=(1\pm Rand\cdot(1-\frac{iter}{iter_{max}}))\odot X_{i} \\ &w_{h}=e^{-\left|\frac{f(X_{i-k})}{f(X_{i+k})+eps}\right|} \\ &Rand=[rand_{1},rand_{2},\ldots,rand_{dim}] \end{aligned}\tag{3} Xinew=Xi+f⋅(Xnear−Xi+np1⋅k=1∑npwh⋅(Xi−k−Xi+k))⊙MfXnear=(1±Rand⋅(1−itermaxiter))⊙Xiwh=e− f(Xi+k)+epsf(Xi−k) Rand=[rand1,rand2,…,randdim](3)
其中𝑋𝑛𝑒𝑎𝑟是附近的位置,“±”表示𝑋𝑛𝑒𝑎𝑟可能与𝑖th原生动物在不同的方向。Xi-k表示从𝑘th配对邻居中选出的i-k原生动物。
休眠行为
在环境压力下,原生动物可能会采取休眠行为作为一种生存策略来忍受不利的条件。当原生动物处于休眠状态时,它会被新产生的原生动物所取代,以保持恒定的种群数量。
X i n e w = X m i n + R a n d ⊙ ( X m a x − X m i n ) X m i n = [ l b 1 , l b 2 , … , l b d i m ] , X m a x = [ u b 1 , u b 2 , … , u b d i m ] (4) \begin{aligned}&X_{i}^{new}=X_{min}+Rand\odot(X_{max}-X_{min})\\&X_{min}=[lb_{1},lb_{2},\ldots,lb_{dim}],\quad X_{max}=[ub_{1},ub_{2},\ldots,ub_{dim}]\end{aligned}\tag{4} Xinew=Xmin+Rand⊙(Xmax−Xmin)Xmin=[lb1,lb2,…,lbdim],Xmax=[ub1,ub2,…,ubdim](4)
繁殖行为
在适当的年龄和健康状况下,原生动物进行无性繁殖,这被称为二元裂变。理论上,这种繁殖会导致原生动物分裂成两个完全相同的子代。我们通过产生一个重复的原生动物并考虑扰动来模拟这种行为。
X i n e w = X i ± r a n d ⋅ ( X m i n + R a n d ⊙ ( X m a x − X m i n ) ) ⊙ M r M r [ d i ] = { 1 , i f d i i s i n r a n d p e r m ( d i m , ⌈ d i m ⋅ r a n d ⌉ ) 0 , o t h e r w i s e (5) \begin{aligned}&X_{i}^{new}=X_{i}\pm rand\cdot(X_{min}+Rand\odot(X_{max}-X_{min}))\odot M_{r}\\&M_{r}[di]=\begin{cases}1,&\mathrm{~if~}di\mathrm{~is~in~}randperm(dim,\lceil dim\cdot rand\rceil)\\0,&\mathrm{~otherwise}\end{cases}\end{aligned}\tag{5} Xinew=Xi±rand⋅(Xmin+Rand⊙(Xmax−Xmin))⊙MrMr[di]={1,0, if di is in randperm(dim,⌈dim⋅rand⌉) otherwise(5)
APO涉及的参数:
p f = p f m a x ⋅ r a n d p a h = 1 2 ⋅ ( 1 + cos ( i t e r i t e r m a x ⋅ π ) ) p d r = 1 2 ⋅ ( 1 + cos ( ( 1 − i p s ) ⋅ π ) ) (6) \begin{aligned} &pf=pf_{max}\cdot rand \\ &p_{ah}={\frac{1}{2}}\cdot(1+\cos({\frac{iter}{iter_{max}}}\cdot\pi)) \\ &p_{dr}={\frac{1}{2}}\cdot(1+\cos((1-{\frac{i}{ps}})\cdot\pi)) \end{aligned}\tag{6} pf=pfmax⋅randpah=21⋅(1+cos(itermaxiter⋅π))pdr=21⋅(1+cos((1−psi)⋅π))(6)
其中pf为原生动物种群中休眠和繁殖的比例分数,pah表示自养和异养行为的概率,pdr表示休眠和繁殖的概率。
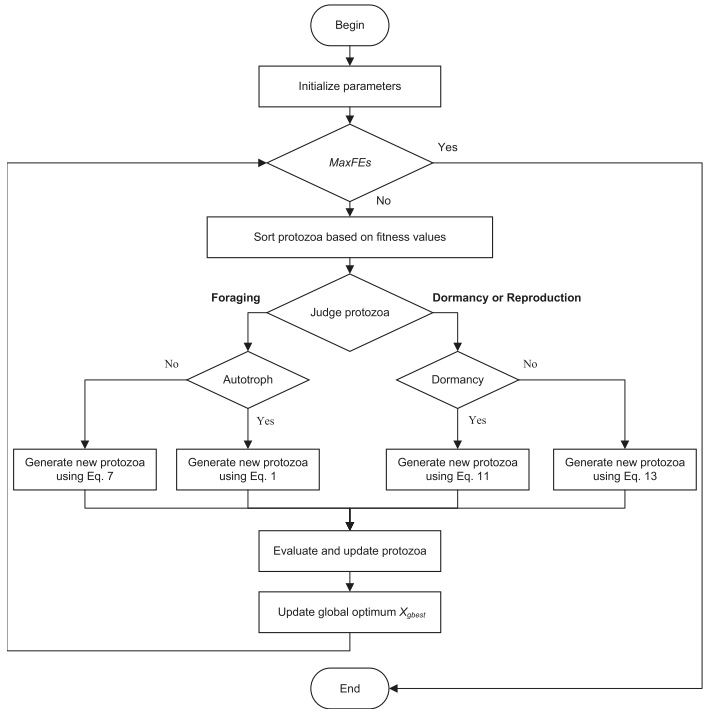
流程图
伪代码

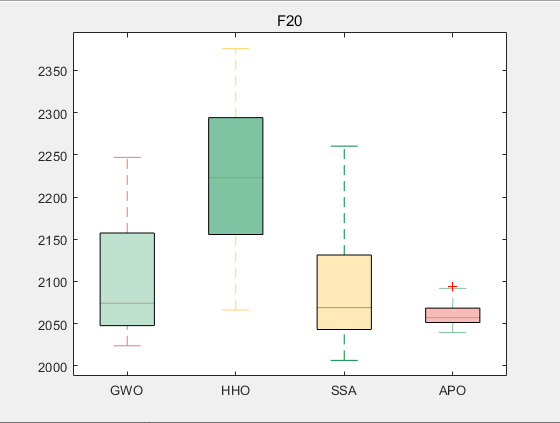
3.结果展示
使用测试框架,测试APO性能 一键run.m
- 【智能算法】省时方便,智能算法统计指标——一键运行~
CEC2017-F20
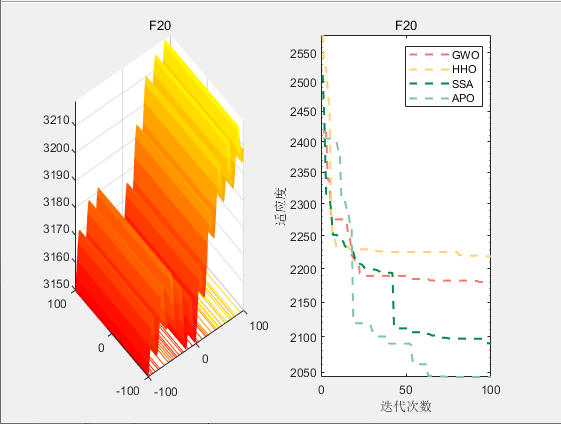

4.参考文献
[1] Wang X, Snášel V, Mirjalili S, et al. Artificial Protozoa Optimizer (APO): A novel bio-inspired metaheuristic algorithm for engineering optimization[J]. Knowledge-Based Systems, 2024: 111737.
5.获取代码
这篇关于【智能算法】人工原生动物优化算法(APO)原理及实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





