本文主要是介绍自动驾驶融合定位系列教程五:惯性导航误差分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
自动驾驶融合定位系列教程五:惯性导航误差分析
一、概述
在定位领域的几乎所有多传感器融合系统中,都有IMU存在,而且,IMU是定位系统的主线与核心(对此可能很多人并不同意,但是我仍然坚定地坚持这一观点)。
对于IMU参与的融合系统(无论是基于滤波还是基于优化),它的误差分析就既是核心内容,也是基础内容,是必须要掌握的。如果要简单解释,所谓融合,就是根据观测误差去反推状态误差,而误差分析就是给出观测误差与状态误差之间的关系,让这个“反推”不再是文字,而具有数学表达,从而可以进行算法实现。
具体来讲,在IMU融合系统中,这里的观测误差就对应位置误差、速度误差、姿态误差,状态误差指的就是位置误差、速度误差、姿态误差、陀螺仪的bias、加速度计的bias等。观测和状态中有重复的量这很正常,说明“有些状态可以被直接观测到”。而根据观测误差去反推状态误差,指的就是,如果告诉你它们之间的关系(比如已知陀螺仪的bias和姿态误差之间的关系),那么就可以根据该关系去反推出那些不能被直接观测到的量(比如已知姿态误差去反推陀螺仪bias)。

附赠自动驾驶学习资料和量产经验:链接
二、误差方程推导思路
误差方程的推导公式还是挺多的,所以,按照本系列文章的风格,会先介绍推导的思路,把公式推导放在思路的框架下理解,以避免陷入混乱状态。
既然误差分析是对观测误差和状态误差关系的推导,那么我们不妨就从一个简单的例子,来把这个推导思路解释清楚。假设z是观测,x和y都是状态,并且有
𝑧˙=𝑥+𝑦
误差分析指的就是,由上面的方程,推导出 𝛿𝑧 与 𝛿𝑥 、 𝛿𝑦 之间的关系。我们按照固定的套路,把推导步骤给固化下来,这样,我们在后面推导位置、速度、姿态的误差方程的时候就直接往上套就行了。整个过程可以分为以下几步:
1)写出不考虑误差时的微分方程
𝑧˙=𝑥+𝑦
2)写出考虑误差时的微分方程
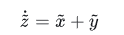
3)写出真实值与理想值之间的关系
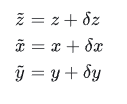
4)把3)中的关系,代入2)
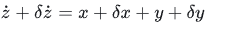
5)把1)中的关系,代入4)
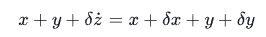
6)化简方程
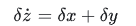
经过这样 6 步,就很容易地达到了我们的目的。不过对于这个方程来讲,有点过于简单了,因为不写出这 6 个步骤,可能也能直接看出答案,但这只是以此为例,把步骤梳理清楚,等真正推导IMU的误差方程的时候,不能直接看得出结果,这些就用得上了。
三、IMU 误差方程推导
1.姿态误差方程
我们以四元数的表达方式为例,进行介绍。同样按照刚才的 6 个步骤往里面套。


根据上一篇文章所讲,四元数相乘可以转换成矩阵与向量相乘
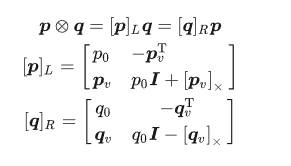
令
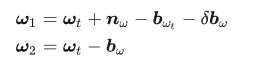
则
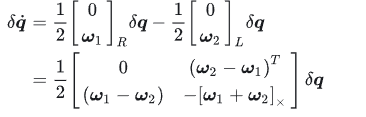
由于融合时,状态量中往往不是使用四元数,而是使用失准角,因此要把上式转成失准角的微分形式。

2.速度误差方程

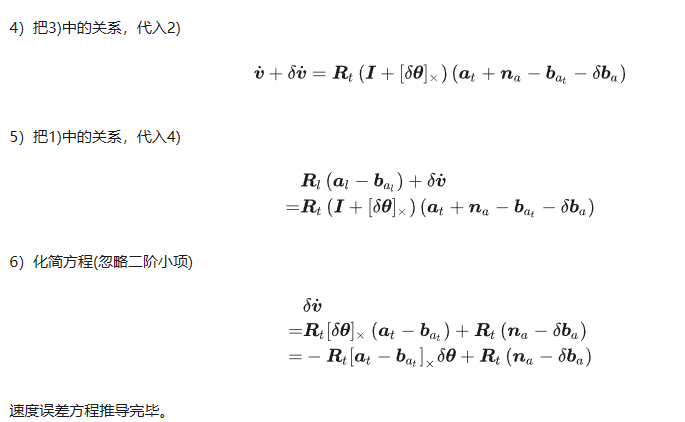
3.位置误差方程推导

位置误差方程推导完毕。
四、总结
可以看出,掌握基本思路以后,推导是不太费脑子的,就是有点费纸。这里啰哩啰嗦把这些东西讲完,后面的章节就直接使用这里的结论了。
这篇关于自动驾驶融合定位系列教程五:惯性导航误差分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






