本文主要是介绍三维SDMTSP:GWO灰狼优化算法求解三维单仓库多旅行商问题,可以更改数据集和起点(MATLAB代码),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、单仓库多旅行商问题
多旅行商问题(Multiple Traveling Salesman Problem, MTSP)是著名的旅行商问题(Traveling Salesman Problem, TSP)的延伸,多旅行商问题定义为:给定一个𝑛座城市的城市集合,指定𝑚个推销员,每一位推销员从起点城市出发访问一定数量的城市,最后回到终点城市,要求除起点和终点城市以外,每一座城市都必须至少被一位推销员访问,并且只能访问一次,需要求解出满足上述要求并且代价最小的分配方案,其中的代价通常用总路程长度来代替,当然也可以是时间、费用等。围绕着各推销员的起始点和终止点来划分,多旅行商问题大致可以分为四种,其中单仓库多旅行商问题是其中一种。多旅行商问题
单仓库多旅行商问题(Single-Depot Multiple Travelling Salesman Problem, SD-MTSP):𝑚个推销员从同一座中心城市出发,访问其中一定数量的城市并且每座城市只能被某一个推销员访问一次,最后返回到中心城市,通常这种问题模型被称之为SD-MTSP。
原文链接:https://blog.csdn.net/weixin_46204734/article/details/133517100
二、灰狼优化算法求解三维单仓库多旅行商问题
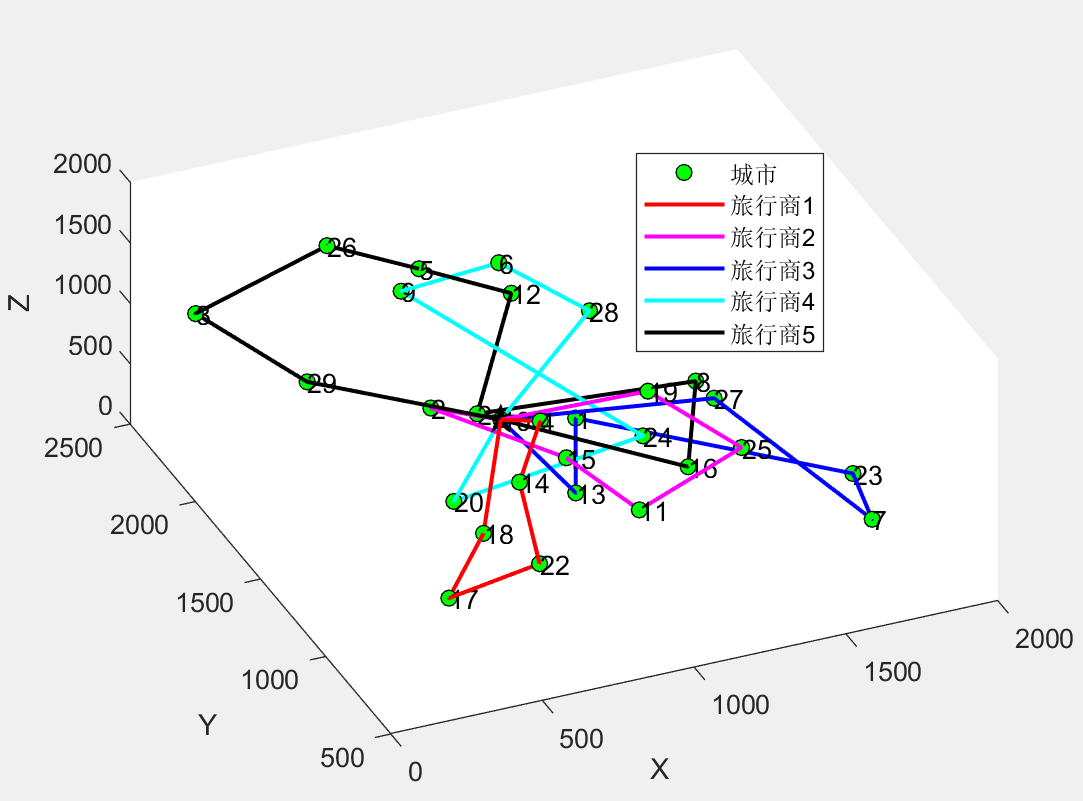
第1个旅行商的路径:10->18->17->22->14->4->10
第1个旅行商的总目标函数值:1063.936088
第2个旅行商的路径:10->19->25->11->15->2->10
第2个旅行商的总目标函数值:1478.896210
第3个旅行商的路径:10->13->1->23->7->27->10
第3个旅行商的总目标函数值:1910.167008
第4个旅行商的路径:10->20->24->9->6->28->10
第4个旅行商的总目标函数值:1762.310983
第5个旅行商的路径:10->29->3->26->5->12->21->8->16->10
第5个旅行商的总目标函数值:2044.103716
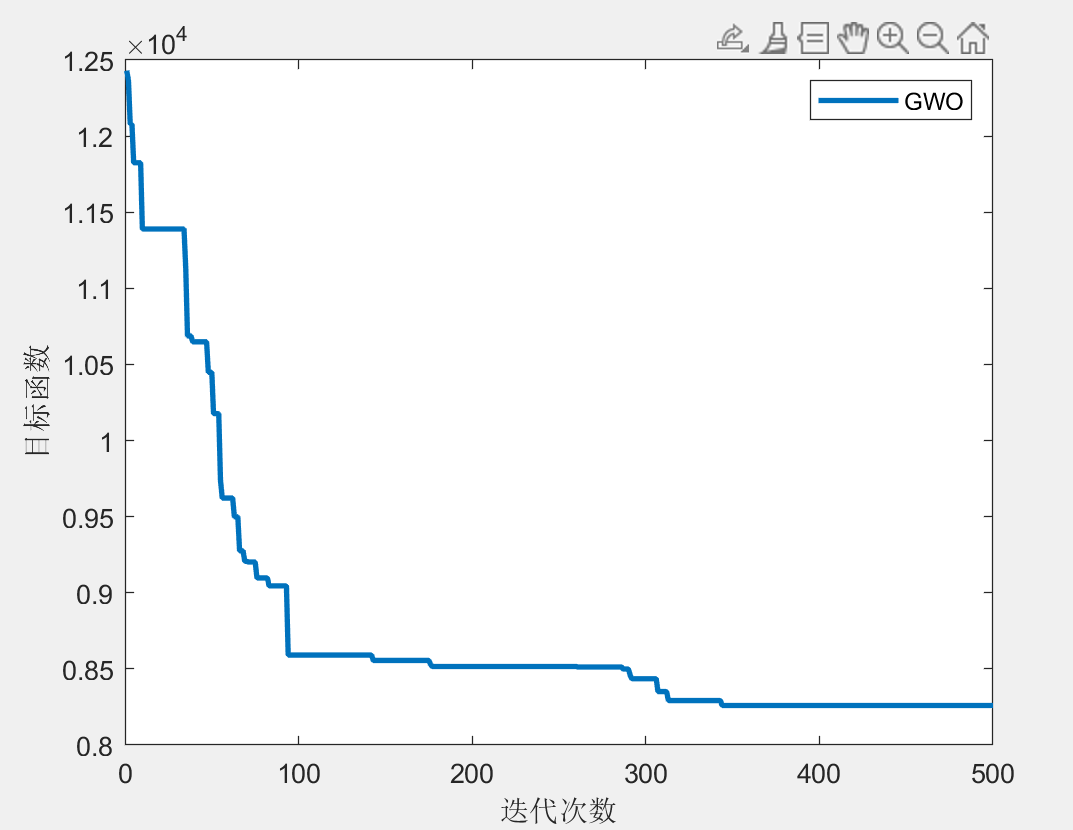
所有旅行商的总目标函数值:8259.414005
三、完整MATLAB代码
这篇关于三维SDMTSP:GWO灰狼优化算法求解三维单仓库多旅行商问题,可以更改数据集和起点(MATLAB代码)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






