本文主要是介绍现代计算机图形学笔记(六)——布林-冯反射模型、图形管线、纹理映射,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
上节课我们讨论了布林-冯模型中的漫反射部分,本节将继续讨论该模型中的高光和环境光部分。
布林-冯反射模型(Blinn-Phong Reflectance Model)
高光
对于模型的高光,我们只可以从镜面反射方向看到,也就是说当我们眼睛看的方向 V \bold{V} V和镜面反射方向 R \bold{R} R很接近时可以看到高光。
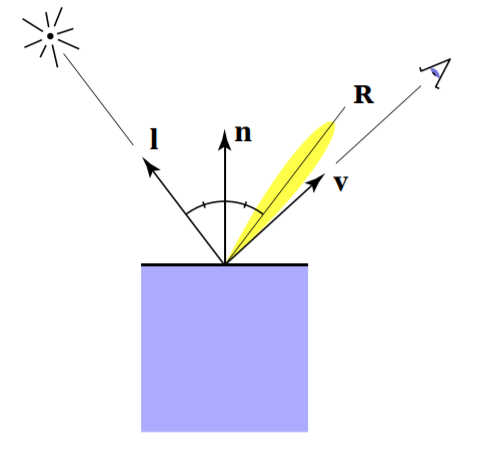
但是我们定义镜面方向有些困难,于是我们引入了半程向量(bisector) h \bold{h} h来定义高光,如下图。如果我们得到的半程向量 h \bold{h} h与法线方向 n \bold{n} n很接近,那么我们就可以看到高光。
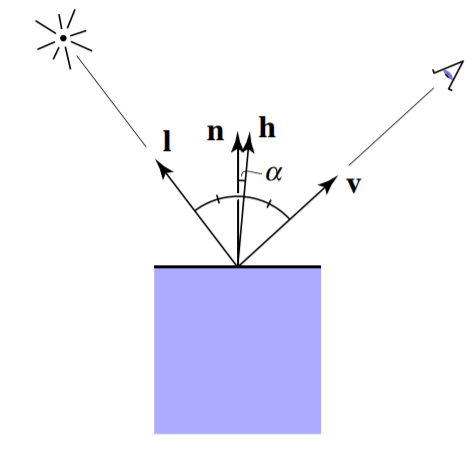
h = bisector ( v , l ) = v + l ∥ v + l ∥ (1) \bold{h}=\text{bisector}(\bold{v},\bold{l})=\frac{\bold{v}+\bold{l}}{\left\| \bold{v}+\bold{l} \right\|} \tag{1} h=bisector(v,l)=∥v+l∥v+l(1)
则我们可以使用半程向量(bisector)来定义高光的能量
L s = k s ( I / r 2 ) max ( 0 , cos α ) p = k s ( I / r 2 ) max ( 0 , n ⋅ h ) p (2) L_s=k_s(I/r^2)\max(0,\cos \alpha)^p\\ =k_s(I/r^2)\max(0,\bold{n}\cdot\bold{h})^p \tag{2} Ls=ks(I/r2)
这篇关于现代计算机图形学笔记(六)——布林-冯反射模型、图形管线、纹理映射的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





