本文主要是介绍Meta·清华·剑桥联合研发树搜索法,优化复杂系统性能提升10-20倍,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
引言:探索高维复杂系统的优化新方法
在现代科学研究和工程设计中,我们经常面临着需要优化高维复杂系统的挑战。这些系统可能包含数以百计甚至数千个参数,而且往往没有明确的数学表达式可以描述它们的行为。传统的基于导数的优化方法在这些情况下往往效果不佳,因为它们通常需要对目标函数做出强假设,并且在处理非凸问题或者维度较高的问题时容易陷入局部最优解。因此,开发一种能够有效应对这些挑战的新方法,对于加速复杂系统的最优设计具有重要意义。
本文介绍了一种新的无导数树搜索方法,用于优化高维复杂系统。该方法通过结合随机树扩展、动态置信上界和短程反向传播机制,有效地避免了局部最优解的陷阱,并利用机器学习模型迭代逼近全局最优解。这一发展有效地解决了维度挑战问题,在多达2000维的各种基准函数上实现了全局最优解的收敛,性能超过现有方法10到20倍。该方法在材料、物理和生物学等多个实际复杂系统中的应用表现出色,显著优于现有的最先进算法。此外,该方法的成功实现还促进了自动化知识发现和自驾虚拟实验室的发展。虽然本文主要关注自然科学领域的问题,但在这里取得的优化技术进步同样适用于更广泛的跨学科挑战。
1. 论文标题:Derivative-free tree optimization for complex systems
2. 作者与机构:清华大学、德国达姆施塔特工业大学、德国慕尼黑赫尔姆霍兹人工智能中心、北京大学、英国剑桥大学等。
3. 论文链接:https://arxiv.org/pdf/2404.04062.pdf
树搜索方法与传统优化技术的对比
1. 传统技术的局限性
传统的导数自由优化技术(Derivative-Free Optimization, DFO)在处理复杂系统的优化问题时,往往依赖于对目标函数的强假设。这些技术在优化非凸系统时表现出明显的不足,尤其是当问题的维度超过100时。在高维空间中,传统方法往往难以逃离局部最优解,导致优化过程陷入停滞。此外,当问题维度进一步增加到200维或更高时,如Rastrigin 1000维、Ackley 200维、Rosenbrock 100维等,传统方法的性能进一步下降,几乎无法收敛到全局最优解。
2. 树搜索方法的创新点
相较于传统技术,树搜索方法(如本文介绍的DOTS)引入了多项创新点,以应对高维优化问题。首先,通过随机树扩展(Stochastic Tree Expansion),该方法能够在不知道目标函数闭合表达式或导数的情况下,探索高维参数空间。其次,动态置信上界(Dynamic Confidence Upper Bound, DUC B)和短程反向传播机制(Short-range Backpropagation)的引入,帮助算法避免陷入局部最优,并迭代逼近全局最优解。这些机制的结合,使得DOTS在多达2000维的各种基准函数上实现了超过90%的收敛率,远超现有方法的10到20倍。此外,通过自适应探索和顶点访问采样,DOTS能够有效地在复杂的真实世界系统中寻找最优解,显著优于现有的先进算法。
高维优化问题的挑战与机遇
1. 高维系统的优化难题
高维优化问题的主要难点在于参数空间的维度爆炸,导致搜索空间急剧增大。在这样的空间中,传统优化算法很难维持有效的搜索效率,因为它们通常无法处理复杂的、非凸的、多峰的目标函数。此外,高维空间中的局部最小值数量众多,使得算法更容易陷入这些局部最小值,而无法找到全局最优解。这些问题在实际应用中尤为突出,比如在材料、物理和生物学领域的设计任务中,往往需要处理高达数千维的参数。
2. 树搜索方法的应对策略
树搜索方法,特别是本文提出的DOTS,通过其独特的策略有效地应对了高维优化问题。通过随机扩展搜索树,DOTS能够在高维空间中进行有效的探索。它利用动态置信上界(DUC B)来指导搜索方向,优先探索那些可能带来更大改进的区域。在每次迭代中,通过短程反向传播机制,DOTS能够从局部最小值中逃逸出来,并在参数空间中构建一个“梯度梯子”,帮助算法攀登至更高的目标函数值。此外,自适应探索保持探索权重与整体真实分布的一致性,进一步提高了算法在复杂景观中的导航能力。这些策略的综合运用,使得DOTS在高维空间中展现出了卓越的优化能力,为解决实际复杂系统的设计任务提供了新的机遇。
树搜索方法的核心机制
在处理高维复杂系统的优化问题时,传统的基于导数的优化方法往往因为缺乏闭合形式的目标函数或其导数而变得不适用。为了克服这一挑战,我们介绍了一种树搜索方法,该方法不依赖于目标函数的导数信息。以下是该方法的核心机制:
1. 随机树扩展
随机树扩展是该方法的基础,它允许算法在不知道目标函数具体形式的情况下,通过随机选择和扩展搜索树的节点来探索解空间。如图1(b)所示,这种扩展方式使得算法能够在高维空间中有效地搜索,并且有助于避免陷入局部最优解。
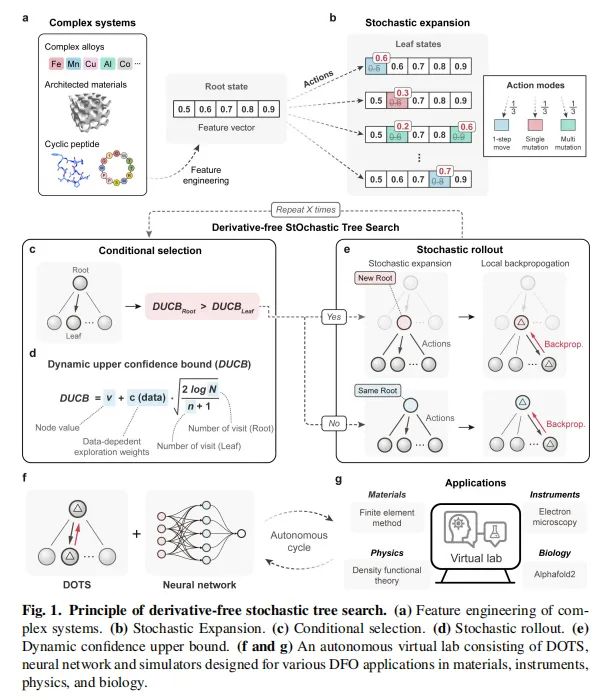
2. 动态置信上界
动态置信上界(Dynamic Confidence Upper Bound, DUCB)是一种用于指导搜索过程的机制。如图1(e)所示,DUCB评估每个节点的潜在价值,并根据这一评估来动态调整搜索方向。这种方法利用了置信区间的概念,通过比较根节点和叶节点的DUCB值,来决定是否继续在当前路径上搜索或是转向其他可能的更优路径。
3. 短程反向传播机制
短程反向传播机制是指在局部区域内使用反向传播来更新节点的评估值,如图1(i)中所示的创建局部DUCB梯度“阶梯”。这种机制有助于算法在平坦的景观中克服局部最小值,从而更接近全局最优解。
实验验证:基准函数与实际应用
为了验证树搜索方法的有效性,我们在基准函数和实际应用中进行了一系列实验。
1. 在多达2000维的基准函数上的表现
我们在不同维度的基准函数上进行了测试,包括Rastrigin 1000维、Ackley 200维和Rosenbrock 100维等。如图2所示,我们的方法在所有合成函数上的收敛率超过了90%,而其他算法则完全无法收敛(0%)。这表明我们的方法在处理高维优化问题时具有显著的优势。
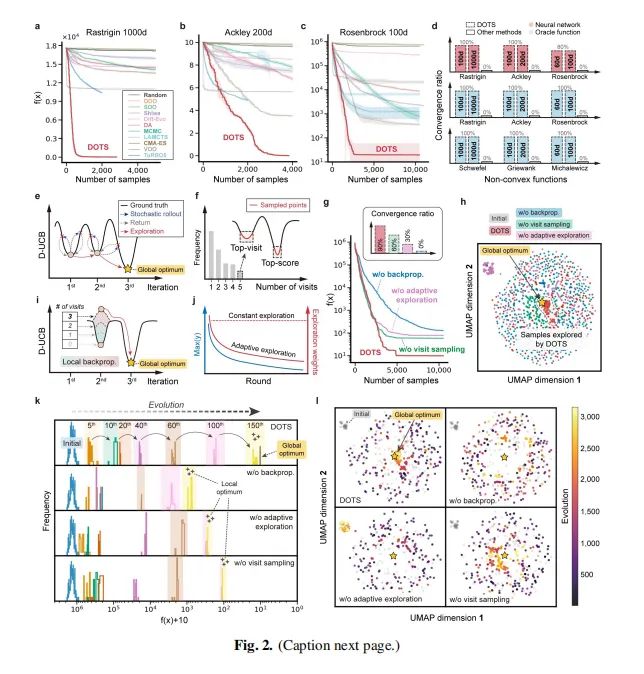
2. 实际复杂系统中的应用案例
我们的方法在多个实际复杂系统中得到了应用,包括材料、物理和生物学领域。例如,图3展示了我们的方法在优化建筑材料的机械性能、电子特性以及蛋白质-蛋白质相互作用(PPIs)方面的应用。在这些案例中,我们的方法不仅在优化性能上显著超越了现有的算法,还展示了通过自驱动的虚拟实验室进行高效自主知识发现的潜力。
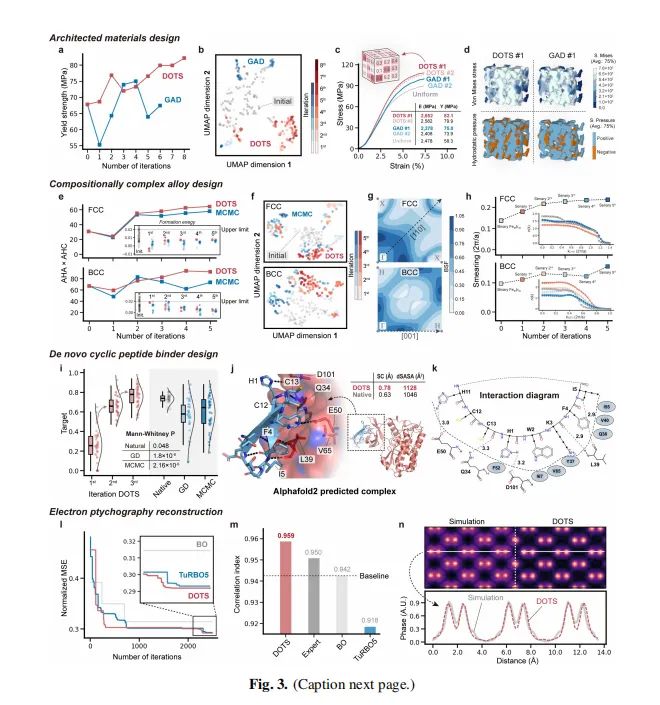
自驾虚拟实验室的构建与应用
1. 材料、物理和生物学领域的应用
自驾虚拟实验室的构建是为了应对高维复杂系统设计任务中的优化问题,这些问题通常涉及到许多参数,而且目标函数的闭合形式或导数未知。在材料科学、物理学和生物学等领域,这种方法已经显示出其强大的应用潜力。例如,在材料科学中,通过使用基于树搜索的导数自由优化方法(DOTS),研究人员能够优化构建材料的机械属性,如图3(a)所示,通过与基线方法GAD的比较,可以看到在输入分布的U-MAP 2D表示中,DOTS方法展现出更优的性能。同样,在优化复杂合金(CCAs)的电子属性时,DOTS与MCMC(基线)方法相比,在费米面的构建上表现出更高的精确度,如图3(e)所示。在生物学领域,DOTS用于优化蛋白-蛋白相互作用(PPIs),并成功设计了通过Alphafold2预测的复合物中的循环肽,如图3(i)所展示。
2. 自动化知识发现的推动作用
自驾虚拟实验室不仅在特定领域内的应用取得了显著成果,而且在自动化知识发现方面也起到了推动作用。通过结合树搜索方法、机器学习模型和模拟器,研究人员能够在没有明确导数信息的情况下,迭代逼近全局最优解。这种方法在处理高维问题时表现出色,如在多达2000维的基准函数上实现了超过90%的收敛率,远超其他现有方法。这种优化技术的进步,不仅加速了复杂系统的最优设计,还促进了高效的自主知识发现,为自驾虚拟实验室的实际应用奠定了基础。
讨论:方法的普适性与跨学科潜力
1. 方法在自然科学领域的影响
在自然科学领域,特别是在材料科学、物理学和生物学中,本文介绍的树搜索方法对于导数自由优化问题的解决具有重要影响。这种方法通过引入随机树扩展、动态置信上界和短程反向传播机制,有效地避免了局部最优,并迭代逼近全局最优。这一发展有效地解决了维度挑战问题,实现了在各种基准函数上的全局最优收敛,显著提高了设计任务的效率和精度。
2. 对其他定量学科的潜在贡献
尽管本文的研究重点在自然科学领域,但所取得的优化技术进步同样适用于更广泛的定量学科挑战。这种方法的普适性和跨学科潜力意味着它可以被应用于任何需要处理高维优化问题的领域,无论是金融工程、运筹学、人工智能还是其他需要精确和高效优化算法的学科。通过这种方法,可以实现更快的自动化决策,推动各个领域的知识发现和技术创新。
总结:树搜索方法的前景与挑战
1. 技术发展的趋势
在众多领域,如材料科学、物理学和生物学,设计任务常常可以归结为在不知道目标函数闭合形式或导数的情况下,寻找其最优解。传统的无导数优化技术(Derivative-Free Optimization, DFO)通常依赖于对目标函数的强假设,这在优化超过100维的非凸系统时常常会失败。然而,最近提出的一种基于树搜索的方法为高维复杂系统的加速最优设计提供了新的可能性。
这种方法通过引入随机树扩展、动态置信上界(Dynamic Upper Confidence Bound, DUCB)和短程反向传播机制,有效地避免了局部最优,并利用机器学习模型迭代逼近全局最优。在实验中,这种方法在多达2000维的各种基准函数上实现了收敛到全局最优,其性能超过了现有方法10到20倍。此外,该方法在真实世界复杂系统中的广泛适用性也得到了验证,显著优于现有的最先进算法。
2. 面临的挑战与未来研究方向
尽管树搜索方法在处理高维优化问题方面取得了显著进展,但仍面临一些挑战。首先,随着维度的增加,算法的性能可能会受到影响,因为高维空间的搜索更加困难,可能导致节点值的不准确。其次,现实世界任务中往往存在大量未标记数据,而标签相对稀缺,这增加了算法在实际应用中的挑战。
未来的研究方向可能包括进一步提高算法在极高维度问题上的鲁棒性和准确性,以及开发更有效的策略来利用未标记数据。此外,算法的适应性和泛化能力也是未来研究的重点,以确保在不同的复杂系统中都能够取得良好的性能。最后,随着自动化实验室和自主知识发现的需求日益增长,如何将树搜索方法与这些系统集成,以实现更高效的自动化设计和优化,也将是一个重要的研究领域。
这篇关于Meta·清华·剑桥联合研发树搜索法,优化复杂系统性能提升10-20倍的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



