本文主要是介绍逻辑回归模型与GBDT+LR——特征工程模型化的开端,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
随着信息技术和互联网的发展, 我们已经步入了一个信息过载的时代,这个时代,无论是信息消费者还是信息生产者都遇到了很大的挑战:
- 信息消费者:如何从大量的信息中找到自己感兴趣的信息?
- 信息生产者:如何让自己生产的信息脱颖而出, 受到广大用户的关注?
为了解决这个矛盾, 推荐系统应时而生, 并飞速前进,在用户和信息之间架起了一道桥梁,一方面帮助用户发现对自己有价值的信息, 一方面让信息能够展现在对它感兴趣的用户前面。 推荐系统近几年有了深度学习的助推发展之势迅猛, 从前深度学习的传统推荐模型(协同过滤,矩阵分解,LR, FM, FFM, GBDT)到深度学习的浪潮之巅(DNN, Deep Crossing, DIN, DIEN, Wide&Deep, Deep&Cross, DeepFM, AFM, NFM, PNN, FNN, DRN), 现在正无时无刻不影响着大众的生活。
推荐系统通过分析用户的历史行为给用户的兴趣建模, 从而主动给用户推荐给能够满足他们兴趣和需求的信息, 能够真正的“懂你”。 想上网购物的时候, 推荐系统在帮我们挑选商品, 想看资讯的时候, 推荐系统为我们准备了感兴趣的新闻, 想学习充电的时候, 推荐系统为我们提供最合适的课程, 想消遣放松的时候, 推荐系统为我们奉上欲罢不能的短视频…, 所以当我们淹没在信息的海洋时, 推荐系统正在拨开一层层波浪, 为我们追寻多姿多彩的生活!
协同过滤模型存在的劣势就是仅利用了用户与物品相互行为信息进行推荐, 忽视了用户自身特征, 物品自身特征以及上下文信息等,导致生成的结果往往会比较片面。
而今天的这两个模型是逻辑回归家族系列, 逻辑回归能够综合利用用户、物品和上下文等多种不同的特征, 生成较为全面的推荐结果。相比于协同过滤和矩阵分解利用用户的物品“相似度”进行推荐, 逻辑回归模型将问题看成了一个分类问题, 通过预测正样本的概率对物品进行排序。这里的正样本可以是用户“点击”了某个商品或者“观看”了某个视频, 均是推荐系统希望用户产生“正反馈”行为。
逻辑回归模型将推荐问题转成成了一个点击率预估问题。协同过滤是“TOPN"推荐的问题, 而逻辑回归转成了一种点击率预估问题, 成了一种二分类, 如果模型预测用户会点击, 那么就进行推荐。
本篇文章会首先介绍逻辑回归模型,易于并行, 模型简单, 训练开销小,由于其局限性引出更为强大的组合模型GBDT+LR, 这个模型利用GBDT的”自动化“特征组合, 使得模型具备了更高阶特征组合的能力,被称作特征工程模型化的开端。
本篇文章的重点在于:GBDT的原理, GBDT的在解决二分类问题上的细节和GBDT+LR模型的细节, 最后是基于GBDT+LR模型完成一个点击率预测的任务。
大纲如下:
- 逻辑回归模型
- GBDT模型的细节介绍
- GBDT+LR模型及及细节
- 编程实践
逻辑回归模型
逻辑回归模型在推荐领域里面, 相比于传统的协同过滤, 能够综合利用用户、物品、上下文等多种不同的特征生成较为“全面”的推荐结果, 而在机器学习领域, 逻辑回归模型是面试当中非常容易被问到的一个算法, 做为神经网络中的最基础单一神经元, 成为了深度学习的基础性结构。
逻辑回归是在线性回归的基础上加了一个Sigmoid 函数(非线形)映射,使得逻辑回归成为一个优秀的分类算法:
逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的。
涉及到了伯努利分布, 极大似然, 梯度下降, 二分类, sigmoid函数,损失函数的推导等。
逻辑回归模型已经将推荐问题转换成了一个点击率预测的问题, 而点击率预测就是一个典型的二分类, 正好适合逻辑回归进行处理, 逻辑回归推荐流程如下:
- 将用户年龄、性别、物品属性、物品描述、当前时间、当前地点等特征转成数值型向量
- 确定逻辑回归的优化目标,比如把点击率预测转换成二分类问题, 这样就可以得到分类问题常用的损失作为目标, 训练模型
- 在预测的时候, 将特征向量输入模型产生预测, 得到用户“点击”物品的概率
- 利用点击概率对候选物品排序, 得到推荐列表
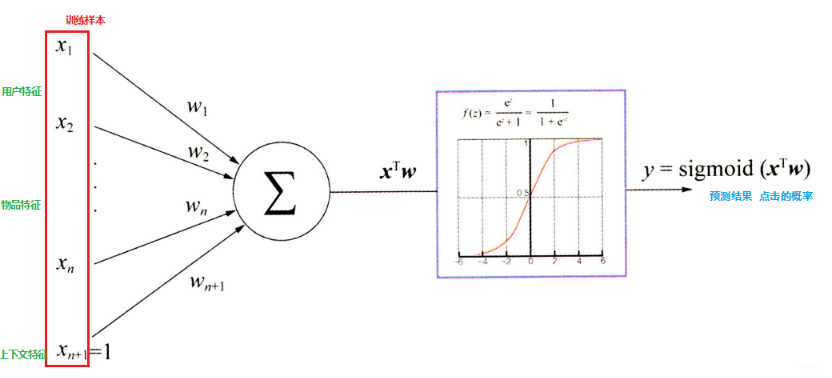
!(https://cdn.mathpix.com/snip/images/ixtRTjccZusk1-XuqxWzK0DXNsul3LDrhywoR0KesEk.original.fullsize.png)
这里的关键就是每个特征的权重参数 w w w ,一般使用梯度下降的方式,先随机初始化一批 w w w ,然后将特征向量(上面数值化出来的特征) 输入到模型,通过计算得到模型的预测概率,然后通过对目标函数求导得到每个 w w w 的梯度,然后进行更 新 w w w,通过若干次迭代, 就可以得到最终的 w w w了
这里的目标函数长下面这样:
J ( w ) = − 1 m ( ∑ i = 1 m ( y i log f w ( x i ) + ( 1 − y i ) log ( 1 − f w ( x i ) ) ) J(w)=-\frac{1}{m}\left(\sum_{i=1}^{m}\left(y^{i} \log f_{w}\left(x^{i}\right)+\left(1-y^{i}\right) \log \left(1-f_{w}\left(x^{i}\right)\right)\right)\right. J(w)=−m1(i=1∑m(yilogfw(xi)+(1−yi)log(1−fw(xi)))
求导之后的方式长这样:
w j ← w j − γ 1 m ∑ i = 1 m ( f w ( x i ) − y i ) x j i w_{j} \leftarrow w_{j}-\gamma \frac{1}{m} \sum_{i=1}^{m}\left(f_{w}\left(x^{i}\right)-y^{i}\right) x_{j}^{i} wj←wj−γm1i=1∑m(fw(xi)−yi)xji
逻辑回归模型的优缺点
优点
- LR模型可解释性好,从特征的权重可以看到不同的特征对最后结果的影响
- 训练时便于并行化,在预测时只需要对特征进行线性加权,适合处理海量id类特征,用id类特征可以防止信息损失(相对于范化的 CTR 特征)
- 资源占用小,尤其是内存。在实际的工程应用中只需要存储权重比较大的特征及特征对应的权重
- 方便输出结果调整。很方便可以最后的分类结果,因为输出的是每个样本的概率分数,可以很容易的对这些概率分数进行cutoff,也就是划分阈值(大于某个阈值的是一类,小于某个阈值的是一类)
- 和复杂模型对比,易于并行化, 模型简单,训练开销小会提升效果
局限性:
- 表达能力不强, 无法进行特征交叉, 特征筛选等一系列操作
- 准确率不高。只是一个线性模型加了个sigmoid,很难去拟合数据的真实分布
- 处理非线性数据较麻烦。 如果想处理非线性, 需要对连续特征离散化(离散化的目的是为了引入非线性),人工分桶
- LR 需要进行人工特征组合,模型迁移起来比较困难,换一个领域又需要重新进行大量的特征工程。
所以如何自动发现有效的特征、特征组合,弥补人工经验不足,缩短LR特征实验周期,是亟需解决的问题, 也正是由于这些问题, 使得推荐系统继续朝着复杂化发展, 衍生出了因子分解机(FM), 组合模型等高维复杂模型, FM模型通过隐变量的方式,发现两两特征之间的组合关系,但这种特征组合仅限于两两特征之间, 这个模型后面也会介绍到。 深度学习时代之后, 多层神经网络凭借着其强大的表达能力替代了逻辑回归, 到现在, 基本上各大公司很少能看到逻辑回归的身影了。
这篇关于逻辑回归模型与GBDT+LR——特征工程模型化的开端的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









