无人驾驶（移动机器人）路径规划之RRT与RRTStar算法及其matlab实现

2024-04-25 23:12
文章标签 算法 规划 matlab 实现 路径 移动机器人 无人驾驶 rrt rrtstar

本文主要是介绍无人驾驶（移动机器人）路径规划之RRT与RRTStar算法及其matlab实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

       在自动驾驶与移动机器人路径规划时，必定会用到经典的算法RRT与RRT Star。下面是RRT与RRTStar的matlab实现效果。可以发现RRTStar效果明显改善。

目录

一、效果比较

1.1 RRT算法效果（黑色为障碍物，红色线为最终路径，蓝色三角形为开始点，粉色三角形为目标点）

1.2 RRTStar算法效果（黑色为障碍物，红色线为最终路径，蓝色三角形为开始点，粉色三角形为目标点）

二、RRT与RRTStar算法

2.1 RRT算法

2.2 RRTStar算法

三、核心代码（完整代码见上述链接）

3.1 地图创建

 3.2 RRT主代码

3.3 RRTStar主代码

3.4 rewire代码。

一、效果比较

1.1 RRT算法效果（黑色为障碍物，红色线为最终路径，蓝色三角形为开始点，粉色三角形为目标点）

代码链接：

移动机器人自主路径规划之RRT算法MATLAB实现代码资源-CSDN文库

（1）原始地图信息。

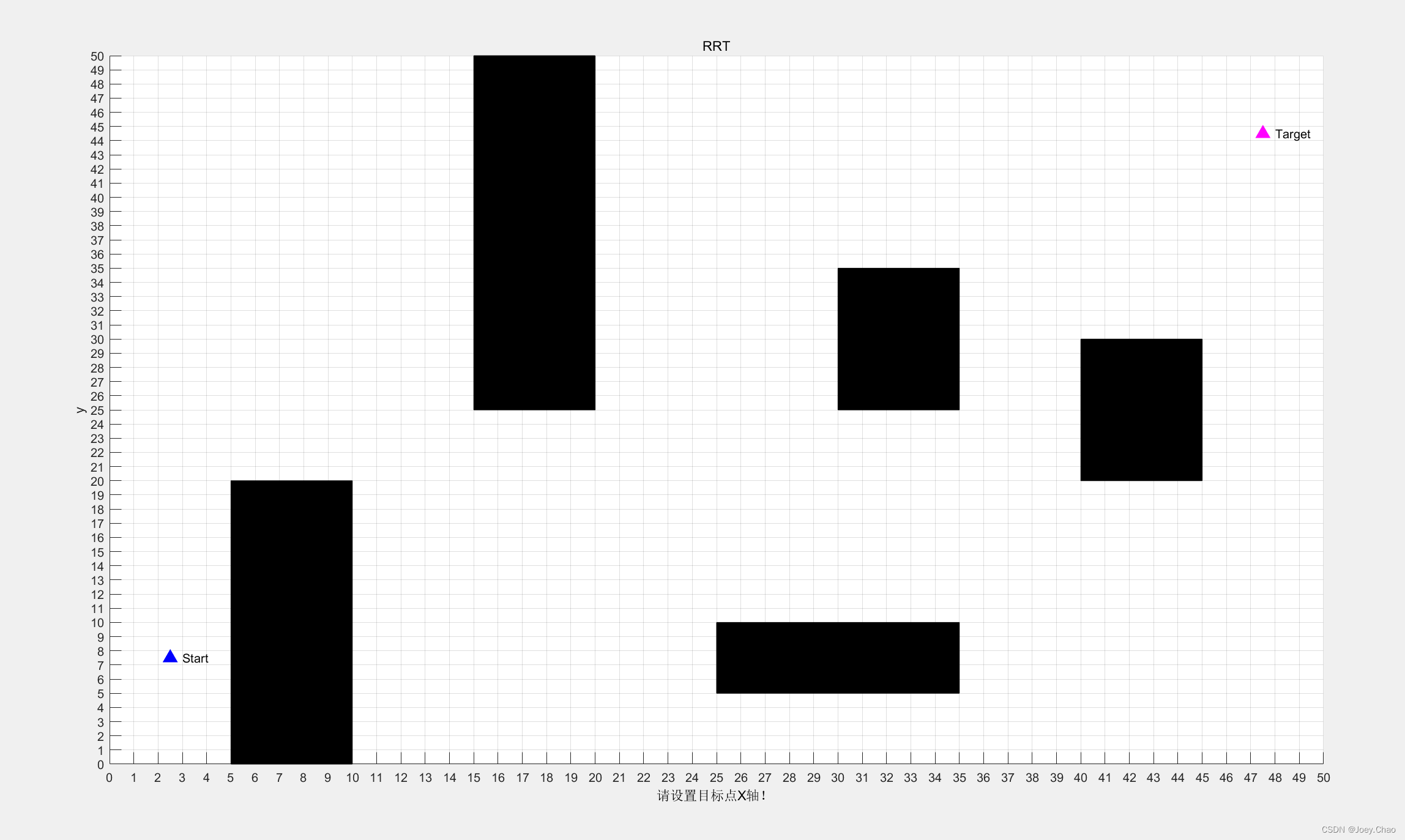
（2）规划路径信息。

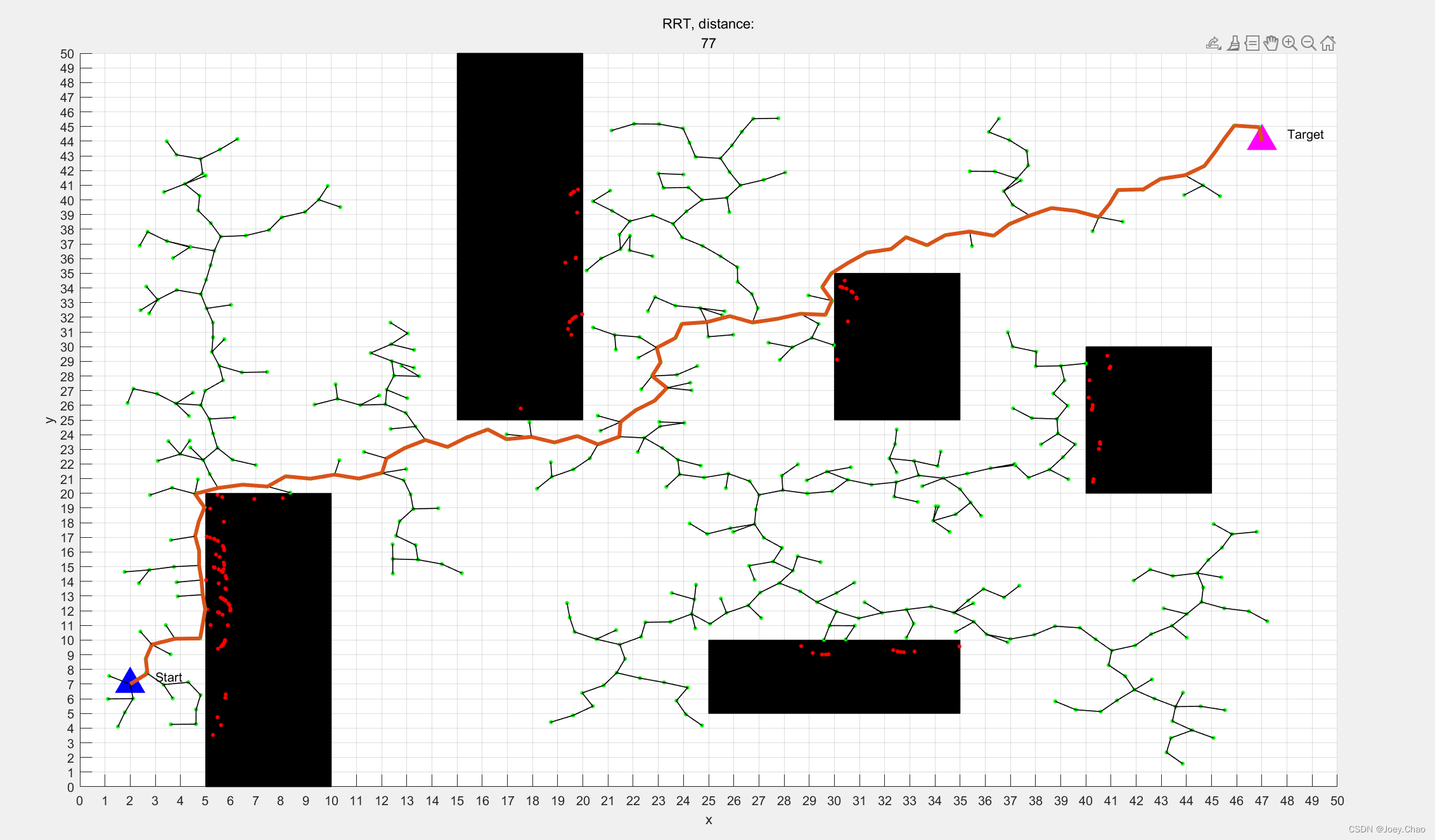
1.2 RRTStar算法效果（黑色为障碍物，红色线为最终路径，蓝色三角形为开始点，粉色三角形为目标点）

代码链接:

移动机器人自主路径规划之RRTStar算法MATLAB实现代码资源-CSDN文库

（1）原始地图信息。

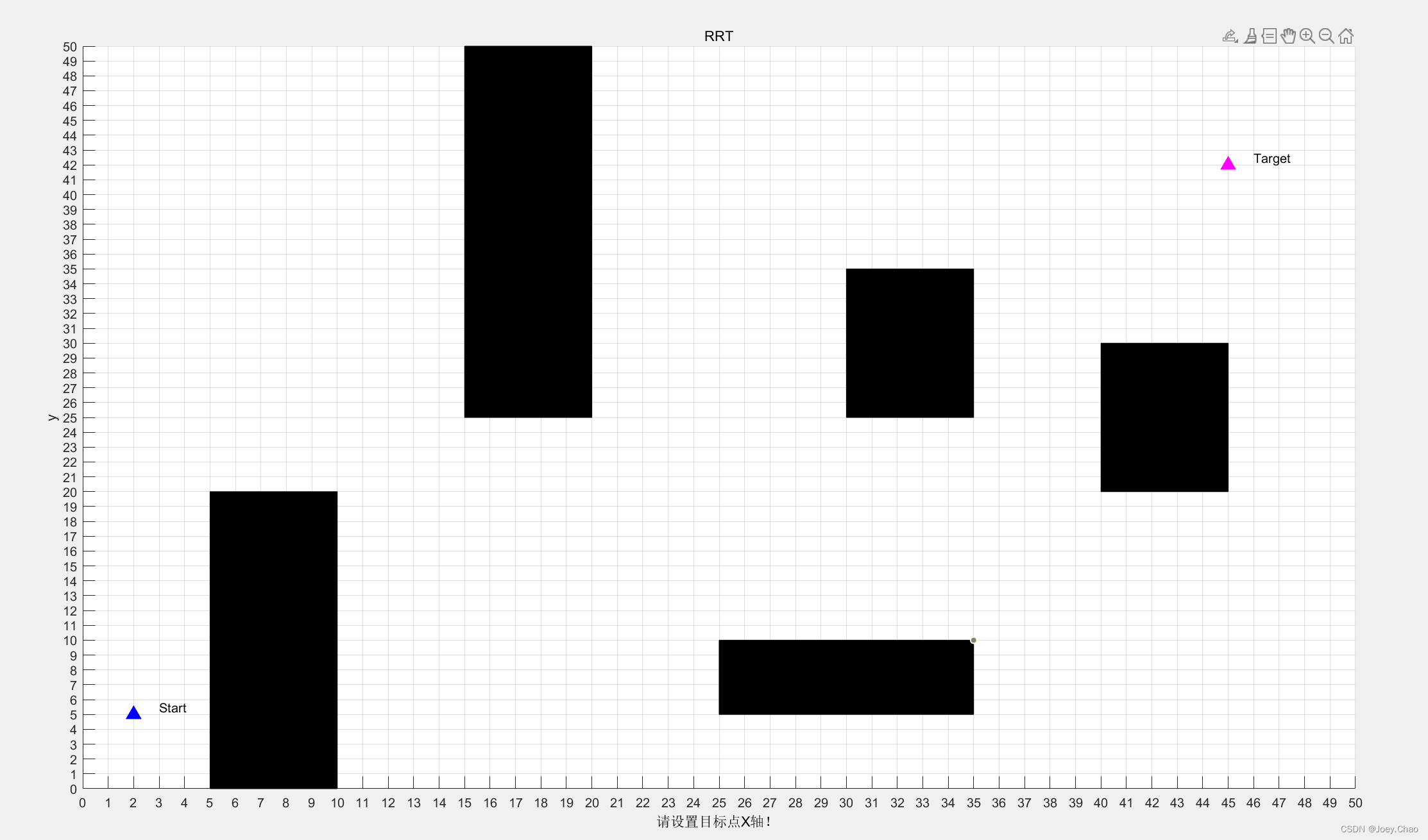
（2）规划路径信息。

 

二、RRT与RRTStar算法

2.1 RRT算法

       RRT算法，全称为Rapidly-Exploring Random Tree（快速探索随机树），是一种在路径规划和运动规划领域广泛应用的算法，特别是在自动驾驶、机器人导航等场景下。该算法由Steven M. LaValle于1998年提出，其核心在于利用随机采样技术构建一个能够快速覆盖配置空间（Configuration Space）的随机树结构，从而找到从初始状态到目标状态的可行路径。

  1. 初始化：算法开始时，从起始点创建一个单一的节点作为随机树的根节点。

  2. 随机采样：算法在每一步中都会随机选取一个状态空间中的点，这个点通常是在整个可行区域或者配置空间中随机产生的。

  3. 接近性判断与树扩展：计算新采样点与树中最近节点的距离，并检查从最近节点沿直线向采样点方向延伸是否遇到障碍物。如果没有障碍阻挡，就在该方向上添加一个新节点至采样点的位置，这个新节点成为树的一部分。

  4. 目标检测与终止条件：如果新添加的节点或采样点落在目标区域，或者与目标点足够接近（依据预设的阈值），则认为找到了一条可行路径，并停止扩展。此时可以通过回溯随机树从起始节点到目标节点来获取路径。

  5. 重复采样与扩展：如果上述步骤未达到终止条件，则重复步骤2至4，直至找到路径或满足其他停止条件（如达到最大迭代次数、计算资源限制等）。

       RRT算法具有概率完备性，即只要存在可行路径，随着迭代次数的增加，算法总能以概率1找到这条路径。然而，RRT算法生成的路径通常不是最优的，且可能包含很多不必要的转折。因此，RRT经常与其他算法（如优化算法）结合使用，以改进路径的质量。

       RRT算法在许多领域都有广泛的应用，包括机器人导航、无人机飞行路径规划、自动驾驶等。它特别适用于那些难以用传统方法（如网格法）处理的复杂环境，能够高效地处理障碍物多且分布不规则的情况。

2.2 RRTStar算法

         RRTStar（Rapidly-exploring Random Tree Star）算法是RRT（Rapidly-exploring Random Tree）算法的一个改进版本，旨在提高路径规划的质量和效率。RRTStar算法继承了RRT算法的基本框架，即通过在空间中随机采样和构建树来探索可行路径。然而，与RRT相比，RRTStar引入了一些关键的改进，使得它在路径优化和避免局部最优解方面更具优势。

以下是RRTStar算法的主要特点和改进之处：

  1. 路径优化：RRTStar算法在构建树的过程中，不仅关注如何快速找到一条从起点到终点的路径，还致力于优化这条路径。它采用了重连策略，即在添加新节点后，会检查是否存在更优的连接方式，如果有，则重新连接树中的节点，以形成更平滑、更短的路径。这种优化过程随着采样点的增加而持续进行，使得最终得到的路径质量更高。

  2. 避免局部最优解：RRT算法有时可能陷入局部最优解，即找到一条看似不错的路径但实际上并不是全局最优的。RRTStar通过引入启发式函数和重新布线策略来避免这个问题。启发式函数用于估计当前节点与目标点之间的距离，引导树的扩展方向，使其更有可能找到全局最优解。重新布线策略则通过调整树的结构，使得路径更加平滑，并减少不必要的转折。

  3. 适应性和鲁棒性：RRTStar算法对不同类型的环境和问题具有较好的适应性和鲁棒性。无论是障碍物分布密集还是稀疏的环境，无论是二维还是三维空间，RRTStar都能有效地进行路径规划。此外，由于它是基于随机采样的方法，因此不依赖于特定的地图表示或环境模型，使得它在实际应用中更加灵活和方便。

       需要注意的是，虽然RRTStar算法在路径优化和避免局部最优解方面表现出色，但它仍然存在一定的局限性。例如，在复杂环境中，RRTStar可能需要较长的计算时间来找到一条满意的路径。此外，由于算法基于随机采样，因此生成的路径可能不是严格的最优解，而是在可接受范围内的次优解。在实际应用中，需要根据具体需求和环境特点来选择合适的算法参数和策略。

      RRT*的实现通常涉及复杂的启发式搜索策略、成本函数的设计以及高效的邻近节点查询机制，比如使用KD树或平衡二叉树来加速最近节点的查找过程，确保算法的高效执行。此外，算法还可能包括对采样策略的优化，以更好地探索环境并避免陷入局部最优。

三、核心代码（完整代码见上述链接）

3.1 地图创建

RRT与RRTStar所用到的地图是相同的。

function [start,target,max_x,max_y,wall,resolution]=creat_map_ob()%创建障碍物地图
%创建地图
clear all;
resolution = 1;%每个格子的长度%map的边界
max_x = 50;
max_y = 50;%obstacle
obstacle(1,:) = [25,5,10,5];
obstacle(2,:) = [15,25,5,25];
obstacle(3,:) = [40,20,5,10];
obstacle(4,:) = [30,25,5,10];
obstacle(5,:) = [5,0,5,20];
figure;%创建新窗口
axis([0 max_x 0 max_y]);
set(gca,'XTick',0:resolution:max_x);%x轴的间隔为1
set(gca,'YTick',0:resolution:max_y);%y轴的间隔为1
grid on;
title('RRT');
xlabel('x');
ylabel('y');
hold on;wall = [obstacle];
for i = 1:1:size(wall,1)fill([wall(i,1),wall(i,1) + wall(i,3),wall(i,1) + wall(i,3),wall(i,1)],...[wall(i,2),wall(i,2),wall(i,2) + wall(i,4),wall(i,2) + wall(i,4)],'k');
end
pause(1);%延时一秒
%初始点
h=msgbox('初始位置标记！');%弹出初始框提示标记初始位置
uiwait(h,3);%3s后关闭对话框
if ishandle(h) == 1%删除对话框delete(h);
end
xlabel('请设置初始点X轴！ ','Color','black');%设置x轴
but = 0;
while(but ~= 1)%收到左键点击[xval,yval,but] = ginput(1);xval=floor(xval);yval=floor(yval);
end
start.x = xval;%初始位置
start.y = yval;
plot(xval,yval,'b^','MarkerFaceColor','b','MarkerSize',10*resolution);%绘制初始点
text(xval + 1,yval + 0.5,'Start');
pause(1);%延时一秒
%目标点
h=msgbox('目标位置标记！');%弹出目标提示标记目标位置
uiwait(h,3);%3s后关闭对话框
if ishandle(h) == 1%删除对话框delete(h);
end
xlabel('请设置目标点X轴！ ','Color','black');%设置x轴
but1 = 0;
while(but1 ~= 1)%收到左键点击[xval,yval,but1] = ginput(1);xval=floor(xval);yval=floor(yval);
end
target.x = xval;%目标位置
target.y = yval;
plot(xval,yval,'m^','MarkerFaceColor','m','MarkerSize',10*resolution);%绘制目标点
text(xval + 1,yval + 0.5,'Target');
hold on;

 3.2 RRT主代码

function RRT()
clc
clear all
close all;
[start,target,max_x,max_y,wall,resolution] = creat_map_ob();
figure;%创建新窗口
axis([0 max_x 0 max_y]);
set(gca,'XTick',0:resolution:max_x);%x轴的间隔为1
set(gca,'YTick',0:resolution:max_y);%y轴的间隔为1
grid on;
title('RRT');
xlabel('x');
ylabel('y');
hold on;
for i = 1:1:size(wall,1)fill([wall(i,1),wall(i,1) + wall(i,3),wall(i,1) + wall(i,3),wall(i,1)],...[wall(i,2),wall(i,2),wall(i,2) + wall(i,4),wall(i,2) + wall(i,4)],'k');
end
plot(start.x,start.y,'b^','MarkerFaceColor','b','MarkerSize',20*resolution);%绘制初始点
text(start.x + 1,start.y + 0.5,'Start');
plot(target.x,target.y,'m^','MarkerFaceColor','m','MarkerSize',20*resolution);%绘制目标点
text(target.x + 1,target.y + 0.5,'Target');
%初始化随机树
tree.child = [];%存储所有节点
tree.parent = [];%存储节点的父节点
tree.distance = [];%存储child到起点的距离tree.child = start;
tree.parent = start;
tree.distance = 0;%存储新衍生的节点，起点初始化
%target_distance用于存储new_node到终点的距离
new_node.x = start.x;
new_node.y = start.y;target_distance = sqrt((target.x-new_node.x)^2+(target.y-new_node.y)^2);
grow_distance = 1;
target_radius = 1.5;
while target_distance > target_radiusrandom_point.x = max_x*rand();random_point.y = max_y*rand();handle1 = plot(random_point.x,random_point.y,'p','MarkerEdgeColor',[0.9290 0.6940 0.1250],'MarkerFaceColor',[0.9290 0.6940 0.1250],'MarkerSize',10*resolution);[angle,min_idx] = find_closet_node(random_point.x,random_point.y,tree);pause(0.001);handle2 = plot([tree.child(min_idx).x,random_point.x],[tree.child(min_idx).y,random_point.y],'-','Color',[0.7 0.7 0.7],'LineWidth',0.8*resolution); %根据步长选择新节点pause(0.001);new_node.x = tree.child(min_idx).x + grow_distance*cos(angle);new_node.y = tree.child(min_idx).y + grow_distance*sin(angle);handle3 = plot(new_node.x,new_node.y,'.r','MarkerFaceColor','r','MarkerSize',10*resolution);obflag = 1;step = 0.01;%判断路径是否位于障碍物之中if new_node.x < tree.child(min_idx).xstep = -step;endfor k = 1:1:size(wall,1)for i = tree.child(min_idx).x:step:new_node.xif angle>pi/2-5e-03 && angle<pi/2+5e-03j = tree.child(min_idx).y+i-tree.child(min_idx).x;elseif angle>-pi/2-5e-03 && angle<-pi/2+5e-03j = tree.child(min_idx).y-i+tree.child(min_idx).x;elsej = tree.child(min_idx).y+(i-tree.child(min_idx).x)*tan(angle);endif i >= wall(k,1) - 0.005 && i <= (wall(k,1)+wall(k,3)) + 0.005if j >= wall(k,2) - 0.005 && j <= (wall(k,2) + wall(k,4)) + 0.005obflag = 0;breakendendendif obflag == 0breakendend%更新pause(0.001);if obflag == 1tree.child(end + 1) = new_node;tree.parent(end + 1) = tree.child(min_idx);tree.distance(end + 1) = 1 + tree.distance(min_idx);target_distance = sqrt((target.x-new_node.x)^2 + (target.y-new_node.y)^2);%删除红色点delete(handle3);plot(new_node.x,new_node.y,'.g','MarkerFaceColor','g','MarkerSize',10*resolution); % draw the new node%画新连接线plot([tree.child(min_idx).x,new_node.x],[tree.child(min_idx).y,new_node.y],'-k','LineWidth',0.8*resolution);endpause(0.001);%删除随机点delete(handle1);%删除最近点与随机点连线。delete(handle2);pause(0.001);
end
tree.child(end + 1) = target;
tree.parent(end + 1) = new_node;
tree.distance(end + 1) = 2 + tree.distance(min_idx);
final_distance = tree.distance(end);
title('RRT, distance:',num2str(final_distance));
current_index = length(tree.child);
while current_index ~= 1plot([tree.child(current_index).x,tree.parent(current_index).x],[tree.child(current_index).y,tree.parent(current_index).y],'-','LineWidth',3*resolution,'Color',[0.8500 0.3250 0.0980]);for i = 1:length(tree.child)if tree.child(i).x == tree.parent(current_index).xif tree.child(i).y == tree.parent(current_index).ycurrent_index = i;breakendendend
end

3.3 RRTStar主代码

function RRT()
clc
clear all
close all;
[start,target,max_x,max_y,wall,resolution] = creat_map_ob();
figure;%创建新窗口
axis([0 max_x 0 max_y]);
set(gca,'XTick',0:resolution:max_x);%x轴的间隔为1
set(gca,'YTick',0:resolution:max_y);%y轴的间隔为1
grid on;
title('RRT');
xlabel('x');
ylabel('y');
hold on;
for i = 1:1:size(wall,1)fill([wall(i,1),wall(i,1) + wall(i,3),wall(i,1) + wall(i,3),wall(i,1)],...[wall(i,2),wall(i,2),wall(i,2) + wall(i,4),wall(i,2) + wall(i,4)],'k');
end
plot(start.x,start.y,'b^','MarkerFaceColor','b','MarkerSize',20*resolution);%绘制初始点
text(start.x + 1,start.y + 0.5,'Start');
plot(target.x,target.y,'m^','MarkerFaceColor','m','MarkerSize',20*resolution);%绘制目标点
text(target.x + 1,target.y + 0.5,'Target');
%初始化随机树
tree.child = [];%存储所有节点
tree.parent = [];%存储节点的父节点
tree.distance = [];%存储child到起点的距离tree.child = start;
tree.parent = start;
tree.distance = 0;
radius = 5;
%存储新衍生的节点，起点初始化
%target_distance用于存储new_node到终点的距离
new_node.x = start.x;
new_node.y = start.y;target_distance = sqrt((target.x-new_node.x)^2+(target.y-new_node.y)^2);
grow_distance = 1;
target_radius = 1.5;line1.l = [];
line1.id = [];
while target_distance > target_radiusrandom_point.x = max_x*rand();random_point.y = max_y*rand();handle1 = plot(random_point.x,random_point.y,'p','MarkerEdgeColor',[0.9290 0.6940 0.1250],'MarkerFaceColor',[0.9290 0.6940 0.1250],'MarkerSize',10*resolution);[angle,min_idx] = find_closet_node(random_point.x,random_point.y,tree);%pause(0.01);handle2 = plot([tree.child(min_idx).x,random_point.x],[tree.child(min_idx).y,random_point.y],'-','Color',[0.7 0.7 0.7],'LineWidth',0.8*resolution); %根据步长选择新节点%pause(0.01);new_node.x = tree.child(min_idx).x + grow_distance*cos(angle);new_node.y = tree.child(min_idx).y + grow_distance*sin(angle);handle3 = plot(new_node.x,new_node.y,'.r','MarkerFaceColor','r','MarkerSize',10*resolution);step = 0.005;%判断路径是否位于障碍物之中%更新pause(0.001);if isobstacle(wall,step,tree,new_node,min_idx,angle) == 1target_distance = sqrt((target.x-new_node.x)^2 + (target.y-new_node.y)^2);%删除红色点delete(handle3);plot(new_node.x,new_node.y,'.g','MarkerFaceColor','g','MarkerSize',10*resolution); % draw the new node%画新连接线handle4 = plot([tree.child(min_idx).x,new_node.x],[tree.child(min_idx).y,new_node.y],'-k','LineWidth',0.8*resolution);% pause(0.001);%删除随机点delete(handle1);%删除最近点与随机点连线。delete(handle2);%pause(0.001);theta = linspace(0, 2*pi, 100);handle6 = plot(new_node.x+radius*cos(theta),new_node.y+radius*sin(theta),'b--');[minid,min_dis_fs,newid] = chooseparent(wall,tree,radius,min_idx,new_node,step,resolution);tree.child(end + 1) = new_node;tree.parent(end + 1) = tree.child(minid);tree.distance(end + 1) = min_dis_fs;delete(handle4);line1.l(end+1) = plot([tree.child(minid).x,new_node.x],[tree.child(minid).y,new_node.y],'-k','LineWidth',0.8*resolution);line1.id(end+1) = length(tree.child);[deid] = rewire(wall,tree,minid,new_node,step,newid,min_dis_fs);if(deid ~= 0)for j = 1:1:length(line1.id)if(line1.id(j) == deid)%pause(2);delete (line1.l(j));breakendend% pause(2);line1.l(j) = plot([tree.child(deid).x,new_node.x],[tree.child(deid).y,new_node.y],'-k','LineWidth',0.8*resolution);%pause(2);enddelete(handle6);else%删除随机点%pause(0.001);delete(handle3);delete(handle1);%删除最近点与随机点连线。delete(handle2);%pause(0.001);endend
tree.child(end + 1) = target;
tree.parent(end + 1) = new_node;
tree.distance(end + 1) = 2 + tree.distance(min_idx);
final_distance = tree.distance(end);
title('RRT, distance:',num2str(final_distance));
current_index = length(tree.child);
while current_index ~= 1plot([tree.child(current_index).x,tree.parent(current_index).x],[tree.child(current_index).y,tree.parent(current_index).y],'-','LineWidth',3*resolution,'Color',[0.8500 0.3250 0.0980]);for i = 1:length(tree.child)if tree.child(i).x == tree.parent(current_index).xif tree.child(i).y == tree.parent(current_index).ycurrent_index = i;breakendendend
end

3.4 rewire代码。

function [deid] = rewire(wall,tree,minid,new_node,step,newid,min_dis_fs)
deid = 0;
for i = 1:1:length(newid)if(newid(i) ~= minid)newcost = min_dis_fs + sqrt((tree.child(newid(i)).x-new_node.x)^2+(tree.child(newid(i)).y-new_node.y)^2);if(newcost < tree.distance(newid(i)))angle = atan2(new_node.y-tree.child(newid(i)).y,new_node.x-tree.child(newid(i)).x);if isobstacle(wall,step,tree,new_node,newid(i),angle) == 1tree.parent(newid(i)) = new_node;tree.distance(newid(i)) = newcost;deid = newid(i);endendend
end

这篇关于无人驾驶（移动机器人）路径规划之RRT与RRTStar算法及其matlab实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/936054。

相关文章

Java实现检查多个时间段是否有重合

Java实现检查多个时间段是否有重合

《Java实现检查多个时间段是否有重合》这篇文章主要为大家详细介绍了如何使用Java实现检查多个时间段是否有重合,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录流程概述步骤详解China编程步骤1：定义时间段类步骤2：添加时间段步骤3：检查时间段是否有重合步骤4：输出结果示例代码结语作
阅读更多...
使用C++实现链表元素的反转

使用C++实现链表元素的反转

《使用C++实现链表元素的反转》反转链表是链表操作中一个经典的问题,也是面试中常见的考题,本文将从思路到实现一步步地讲解如何实现链表的反转,帮助初学者理解这一操作,我们将使用C++代码演示具体实现,同... 目录问题定义思路分析代码实现带头节点的链表代码讲解其他实现方式时间和空间复杂度分析总结问题定义给定
阅读更多...
Java覆盖第三方jar包中的某一个类的实现方法

Java覆盖第三方jar包中的某一个类的实现方法

《Java覆盖第三方jar包中的某一个类的实现方法》在我们日常的开发中,经常需要使用第三方的jar包,有时候我们会发现第三方的jar包中的某一个类有问题,或者我们需要定制化修改其中的逻辑,那么应该如何... 目录一、需求描述二、示例描述三、操作步骤四、验证结果五、实现原理一、需求描述需求描述如下：需要在
阅读更多...
如何使用Java实现请求deepseek

如何使用Java实现请求deepseek

《如何使用Java实现请求deepseek》这篇文章主要为大家详细介绍了如何使用Java实现请求deepseek功能,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录1.deepseek的api创建2.Java实现请求deepseek2.1 pom文件2.2 json转化文件2.2
阅读更多...
python使用fastapi实现多语言国际化的操作指南

python使用fastapi实现多语言国际化的操作指南

《python使用fastapi实现多语言国际化的操作指南》本文介绍了使用Python和FastAPI实现多语言国际化的操作指南,包括多语言架构技术栈、翻译管理、前端本地化、语言切换机制以及常见陷阱和... 目录多语言国际化实现指南项目多语言架构技术栈目录结构翻译工作流1. 翻译数据存储2. 翻译生成脚本
阅读更多...
如何通过Python实现一个消息队列

如何通过Python实现一个消息队列

《如何通过Python实现一个消息队列》这篇文章主要为大家详细介绍了如何通过Python实现一个简单的消息队列,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录如何通过 python 实现消息队列如何把 http 请求放在队列中执行1. 使用 queue.Queue 和 reque
阅读更多...
Python如何实现PDF隐私信息检测

Python如何实现PDF隐私信息检测

《Python如何实现PDF隐私信息检测》随着越来越多的个人信息以电子形式存储和传输,确保这些信息的安全至关重要,本文将介绍如何使用Python检测PDF文件中的隐私信息,需要的可以参考下... 目录项目背景技术栈代码解析功能说明运行结php果在当今，数据隐私保护变得尤为重要。随着越来越多的个人信息以电子形
阅读更多...
使用 sql-research-assistant进行 SQL 数据库研究的实战指南(代码实现演示)

使用 sql-research-assistant进行 SQL 数据库研究的实战指南(代码实现演示)

《使用sql-research-assistant进行SQL数据库研究的实战指南(代码实现演示)》本文介绍了sql-research-assistant工具,该工具基于LangChain框架,集... 目录技术背景介绍核心原理解析代码实现演示安装和配置项目集成LangSmith 配置（可选）启动服务应用场景
阅读更多...
使用Python快速实现链接转word文档

使用Python快速实现链接转word文档

《使用Python快速实现链接转word文档》这篇文章主要为大家详细介绍了如何使用Python快速实现链接转word文档功能,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 演示代码展示from newspaper import Articlefrom docx import
阅读更多...
前端原生js实现拖拽排课效果实例

前端原生js实现拖拽排课效果实例

《前端原生js实现拖拽排课效果实例》：本文主要介绍如何实现一个简单的课程表拖拽功能,通过HTML、CSS和JavaScript的配合,我们实现了课程项的拖拽、放置和显示功能,文中通过实例代码介绍的... 目录1. 效果展示2. 效果分析2.1 关键点2.2 实现方法3. 代码实现3.1 html部分3.2
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2