线性代数 --- 矩阵的对角化以及矩阵的n次幂

本文主要是介绍线性代数 --- 矩阵的对角化以及矩阵的n次幂，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

矩阵的对角化以及矩阵的n次幂

（特征向量与特征值的应用）

前言：

在上一篇文章中，我记录了学习矩阵的特征向量和特征值的学习笔记，所关注的是那些矩阵A作用于向量x后，方向不发生改变的x(仅有尺度的缩放)。
线性代数 --- 特征值与特征向量（上）-CSDN博客文章浏览阅读1.1k次，点赞9次，收藏21次。文章介绍了特征向量与特征值的基本概念，并给出了详细的说明图示和例子。至于如何求解矩阵的特征向量与特征值，我在下一篇文章中给出了说明。https://blog.csdn.net/daduzimama/article/details/136455766
此外，我也在另一篇文章中提到了一般矩阵的特征值与特征向量的求法。线性代数 --- 特征值与特征向量（下）-CSDN博客文章浏览阅读1.3k次，点赞31次，收藏19次。本文介绍了求解一般矩阵的特征向量和特征值的具体方法。https://blog.csdn.net/daduzimama/article/details/136608493

正文：

Part I 矩阵的对角化

这里，我打算通过这篇文章整理/梳理一下矩阵对角化的学习笔记。既然已经知道了如何求出矩阵的特征向量和特征值现，那么找到这些东西有什么用呢？答案就是矩阵的对角化。

(截图来自于参考文献2)

假设一个n维方阵A经过计算后得到n个线性无关的特征向量x1，x2...，xn，对应n个λ1，λ2...，λn。我们有：

$\left\{\begin{matrix} Ax_{1}=\lambda x_{1}\\ Ax_{2}=\lambda x_{2}\\ ...\\ Ax_{n}=\lambda x_{n} \end{matrix}\right.$

现在，我们把这些特征向量都放到一个矩阵中，合成一个新的矩阵X。看看矩阵A乘以矩阵X后会怎么样。首先，我们按照如下方式构建一个新矩阵X，我们称之为特征向量矩阵(Eigen-vector matrix)。因为该矩阵的每一列都是一个特征向量 $x_{i}$ ，所以用大写的X表示：

$X=\begin{bmatrix} | & | & &| \\ | & | & & | \\ x_{1} & x_{2} &... &x_{n} \\ | & | & & | \\ | & | & & | \end{bmatrix}$

令A乘以X，根据矩阵的乘法原则，矩阵A与矩阵X的乘法可以看成是把矩阵X各列看成权重的线性组合的结果(这句话不好懂，可以看看下面的图示)

得到：

$AX=A\begin{bmatrix} | & | & &| \\ | & | & & | \\ x_{1} & x_{2} &... &x_{n} \\ | & | & & | \\ | & | & & | \end{bmatrix}=\begin{bmatrix} | & | & &| \\ | & | & & | \\ Ax_{1} & Ax_{2} &... &Ax_{n} \\ | & | & & | \\ | & | & & | \end{bmatrix}$

$=\begin{bmatrix} | & | & &| \\| & | & &| \\ \lambda _{1}x_{1} & \lambda _{2}x_{2} &... &\lambda _{n}x_{n} \\ | & | & & | \\ | & | & & | \end{bmatrix}=\begin{bmatrix} | & | & &| \\ | & | & &| \\ x_{1} & x_{2} &... &x_{n} \\ | & | & & | \\ | & | & & | \end{bmatrix}\begin{bmatrix} \lambda _{1} &0 &... &0 \\0 & \lambda _{2} &... &0 \\... & ...&... & ...\\ 0 & 0&... & 0\\ 0 & 0 &... & \lambda _{n} \end{bmatrix}$

注意，之前用特征向量构造的新矩阵X，又再一次出现了。与此同时，他的旁边出现了一个新矩阵，这是一个对角矩阵，主对角线上的元素全是特征值λ。这也是一个新矩阵，称之为特征值矩阵(Eigen-value matrix)。因其主对角线上的元素都是特征值 $\lambda _{i}$ ，所以用大写的 $\Lambda$ （即，大写的λ）表示：

$\Lambda =\begin{bmatrix} \lambda _{1} &0 &... &0 \\0 & \lambda _{2} &... &0 \\... & ...&... & ...\\ 0 & 0&... & 0\\ 0 & 0 &... & \lambda _{n} \end{bmatrix}$

最终得到：

$AX=\begin{bmatrix} | & | & &| \\ | & | & &| \\ x_{1} & x_{2} &... &x_{n} \\ | & | & & | \\ | & | & & | \end{bmatrix}\begin{bmatrix} \lambda _{1} &0 &... &0 \\0 & \lambda _{2} &... &0 \\... & ...&... & ...\\ 0 & 0&... & 0\\ 0 & 0 &... & \lambda _{n} \end{bmatrix}=X\Lambda$

The Key Equation

$AX=X\Lambda$

又因为，我之前所构建的特征向量矩阵X是由n个线性无关的特征向量组成的，列与列之间线性无关。因此，矩阵X是可逆的。现在我们把等式两边同时左乘一个X的逆矩阵，即完成了矩阵A的对角化：

$\mathbf{X^{-1}AX=X^{-1}X\Lambda=\Lambda}$

（对角化公式）

反过来，如果把等式两边同时右乘X的逆矩阵，就得到了矩阵A的又一种分解公式（之前学过的分解有基于高斯消元的LU分解，基于gram-schmidt正交化的QR分解）：

$\mathbf{AXX^{-1}=X\Lambda X^{-1}\Rightarrow A=X\Lambda X^{-1}}$

（矩阵A的分解公式）

注意，这一切操作都基于一个前提：矩阵A有n个线性无关的特征向量

什么样的矩阵可以对角化？

当n维方阵A有n个不同的特征值时，矩阵A才能用上述方式对角化。因为，如果A有n个不同的特征值，那么一定对应有n个相互独立的特征向量。但反过来就不一定成立，比如说单位矩阵有n个不同的特征向量，但他的特征值都是1。

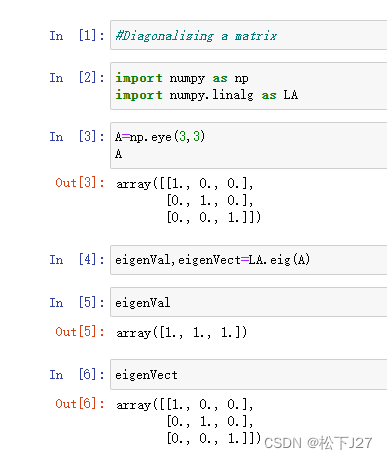
(截图来自于我用Jupyter notebook所生成的代码)

最后我们给出一个矩阵对角化的例子作为这部分的小结，假设方阵矩阵A为：

$A=\begin{bmatrix} 1 &5 \\ 0 & 6 \end{bmatrix}$

首先，用jupyter note book求出特征向量和特征值：

为了方便，我把后面那个特征向量改成[1,1]（我这里不是乱改的，如果自己动手算也能得到这个结果）。如此一来我们得到的两个特征值和他们各自对应的特征向量为：

$\lambda _{1}=1,x_{1}=\begin{bmatrix} 1\\ 0 \end{bmatrix}$ 和 $\lambda _{2}=6,x_{2}=\begin{bmatrix} 1\\ 1 \end{bmatrix}$

相应的在这里我们就能写出特征值矩阵 $\Lambda$ ：

$\Lambda =\begin{bmatrix} \lambda 1 & 0\\ 0 & \lambda 2 \end{bmatrix}=\begin{bmatrix} 1 & 0\\ 0 & 6 \end{bmatrix}$

齐次，用特征向量构建特征向量矩阵X：

$X=\begin{bmatrix} | & |\\ x_{1} &x_{2} \\ |& | \end{bmatrix}=\begin{bmatrix} 1 &1\\ 0 &1 \end{bmatrix}$

求特征向量矩阵X的逆：

$X^{-1}=\begin{bmatrix} 1 &-1 \\ 0& 1 \end{bmatrix}$

代入矩阵的对角化公式完成对角化，看乘法的结果是否正好等于特征向量矩阵 $\Lambda$ ：

$X^{-1}AX=\begin{bmatrix} 1 &-1 \\ 0& 1 \end{bmatrix}\begin{bmatrix} 1 &5 \\ 0& 6 \end{bmatrix}\begin{bmatrix} 1 &1 \\ 0& 1 \end{bmatrix}=\begin{bmatrix} 1 &0 \\ 0& 6 \end{bmatrix}$