本文主要是介绍[运动规划算法]基于似然场的快速避障算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、简介
- 二、原理
- 1. 问题描述
- 2. 概率模型
- 3. 局部概率
- 4. 全局概率
- 5. 方法实现
- 三、项目演示
- 参考
一、简介
这是一种在复杂环境中实现快速自主飞行的规划方法。通常,在复杂环境中进行自主导航需要在栅格地图上进行连续搜索,但是导航过程中通过传感器数据来对图进行更新的计算代价是昂贵的,路径规划也是一样,特别是要求搜索出的路径必须是运动学上可行的。我们建议尽量避免在线搜索来减少计算的复杂度。
首先,要对环境进行建模,使障碍物在传感器探测范围内确定性已知,传感器范围以外概率已知,该方法并非寻找代价最低的路径,而是最大化确定能成功导航到下一个目标的可能性。
该方法支持使用或者不使用先验地图的两种配置。两种配置均可用于运动规划。后者可以允许设定特定目标点或者人工指引来进行导航。
在实验中,它使轻型无人机能够在复杂的森林环境中以10m/s的速度飞行。
二、原理
1. 问题描述
定义: Q ⊂ R Q⊂R Q⊂R表示为车辆的配置空间, A ⊂ Q A⊂Q A⊂Q表示车辆的当前位置, B ⊂ Q B⊂Q B⊂Q表示目标点的位置,起始状态表示 X s X_s Xs,到达目标点B的概率表示为 P B ( . ) P_B(.) PB(.)。
整个规划问题可以描述为:
给定 A 、 B ∈ Q A、B∈ Q A、B∈Q, S ⊂ Q S ⊂ Q S⊂Q及在 Q Q Q中的障碍物,通过初始状态 X s X_s Xs来最大化概率 P B ( X s ) P_B(X_s) PB(Xs)。
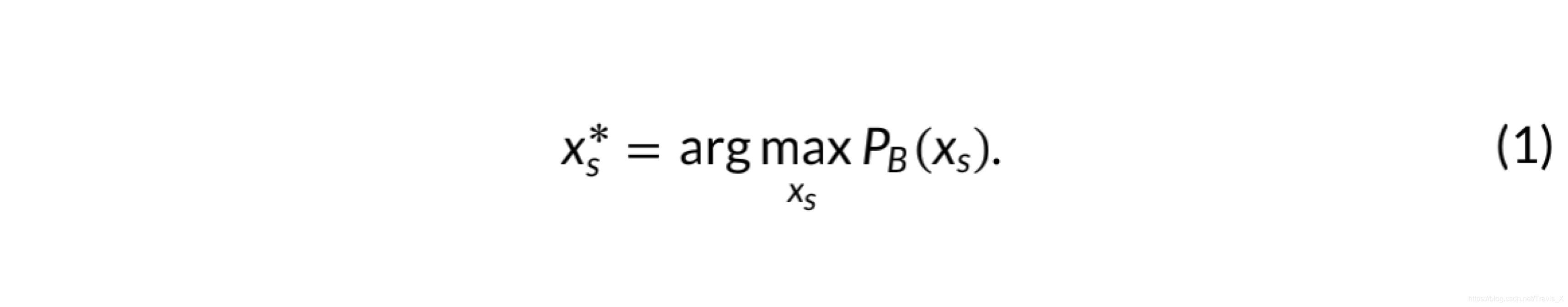
2. 概率模型
根据问题定义中所述,传感器范围 S S S内的障碍物被确定认为是已知的。如果有地图可用,则S以外的障碍物被认为是概率已知的。否则,则认为是没有先验障碍。
将 S S S表示为灰色区域。 F ⊂ S F ⊂ S F⊂S为传感器边界(红色实线表示)。给定初始状态 X s X_s Xs,A和B点连接的路径为黑色曲线。对于所有可能的路径,它们必定与 F F F相交。
定义车辆通过F时的状态为 X f X_f Xf。给定为 X f X_f Xf和 P ( X F ∣ X s ) P (X_F | X_s) P(XF∣Xs)的条件分布可以从传感器提供的障碍信息中得出。此外,可以从先验地图上的障碍物获得车辆从 X f X_f Xf到达B的概率密度 ρ B ( X f ) \rho B(X_f) ρB(Xf)。
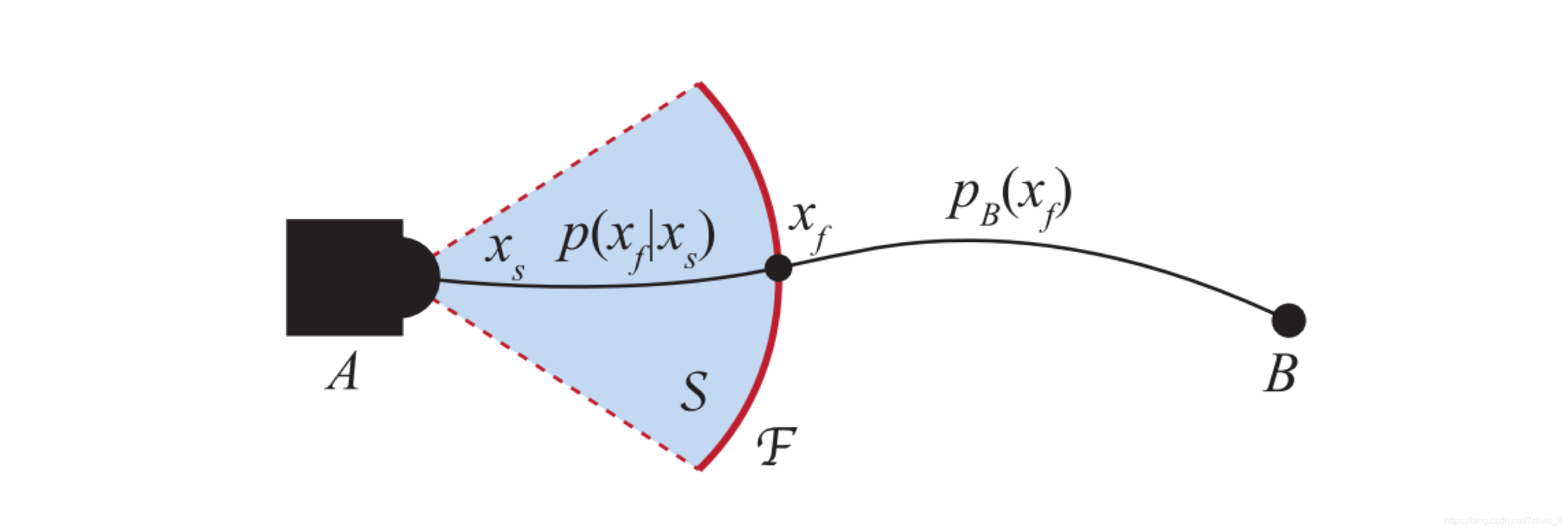
车辆从 X f X_f Xf到达B的概率密度 ρ B ( X f ) \rho B(X_f) ρB(Xf)可以表示为:
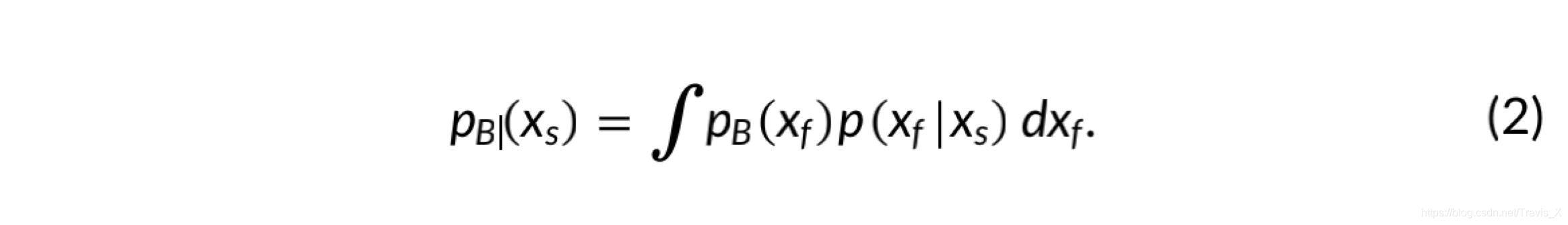
根据蒙特卡洛抽样理论,可以建立:
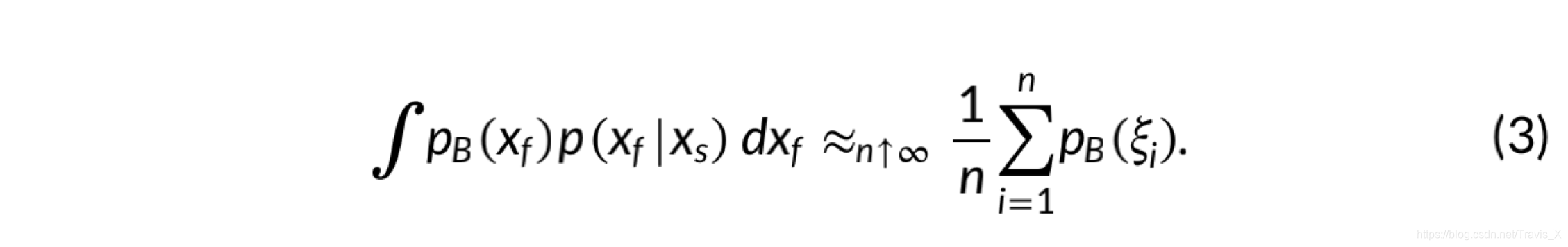
合并公式(2)和(3)以及假定n是一个常数可得:
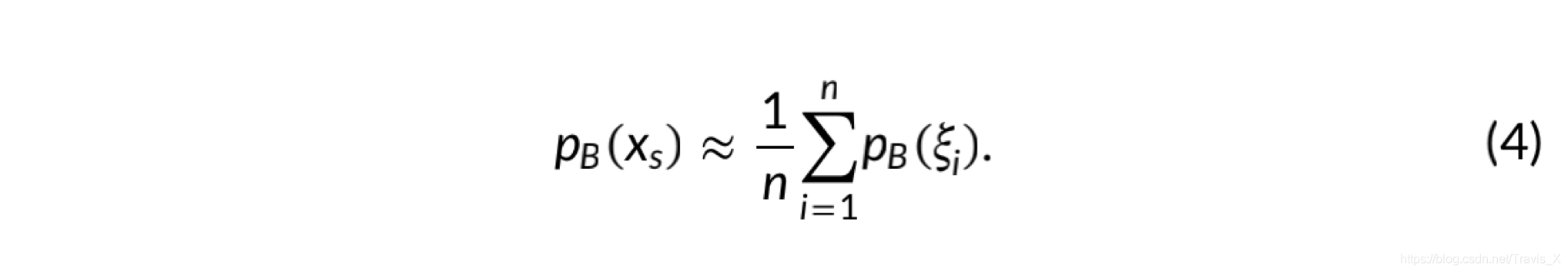
3. 局部概率
给定了初始状态 X s X_s Xs,车辆可以沿着不同的路径到达传感器边界 F F F。
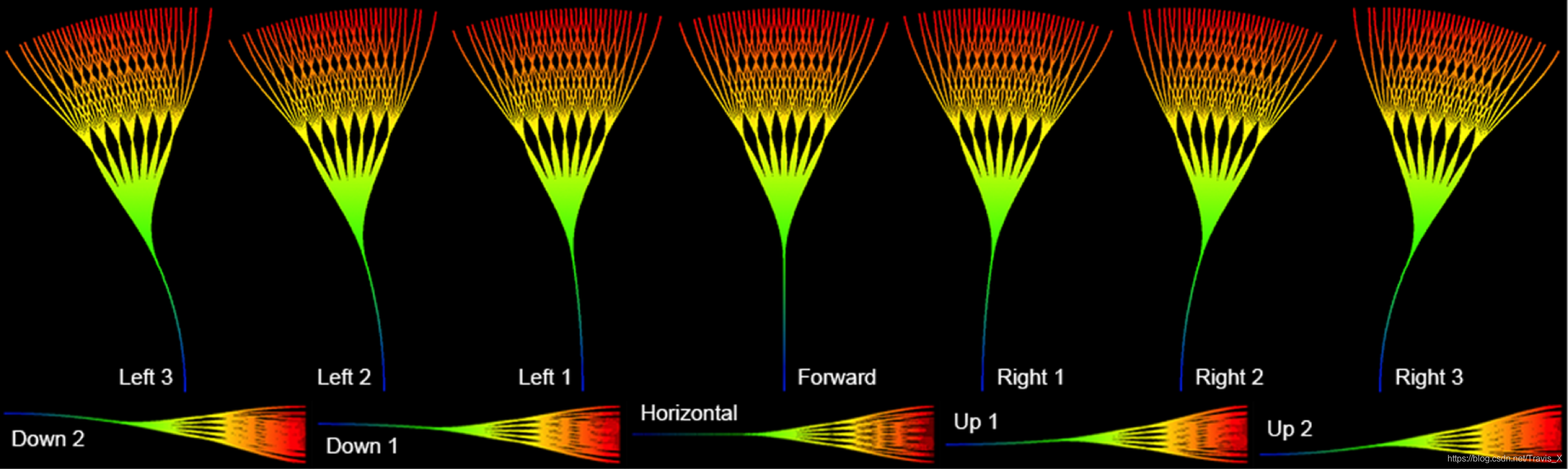
图中所有路径均由三次样条曲线生成,路径首先在35个方向(水平7个,垂直5个方向)上分割,每个路径又在35个方向上分割。这导致一组中的 3 5 2 35^2 352= 1225条路径。考虑35个路径组,总共有35×1225 = 42,875条路径。
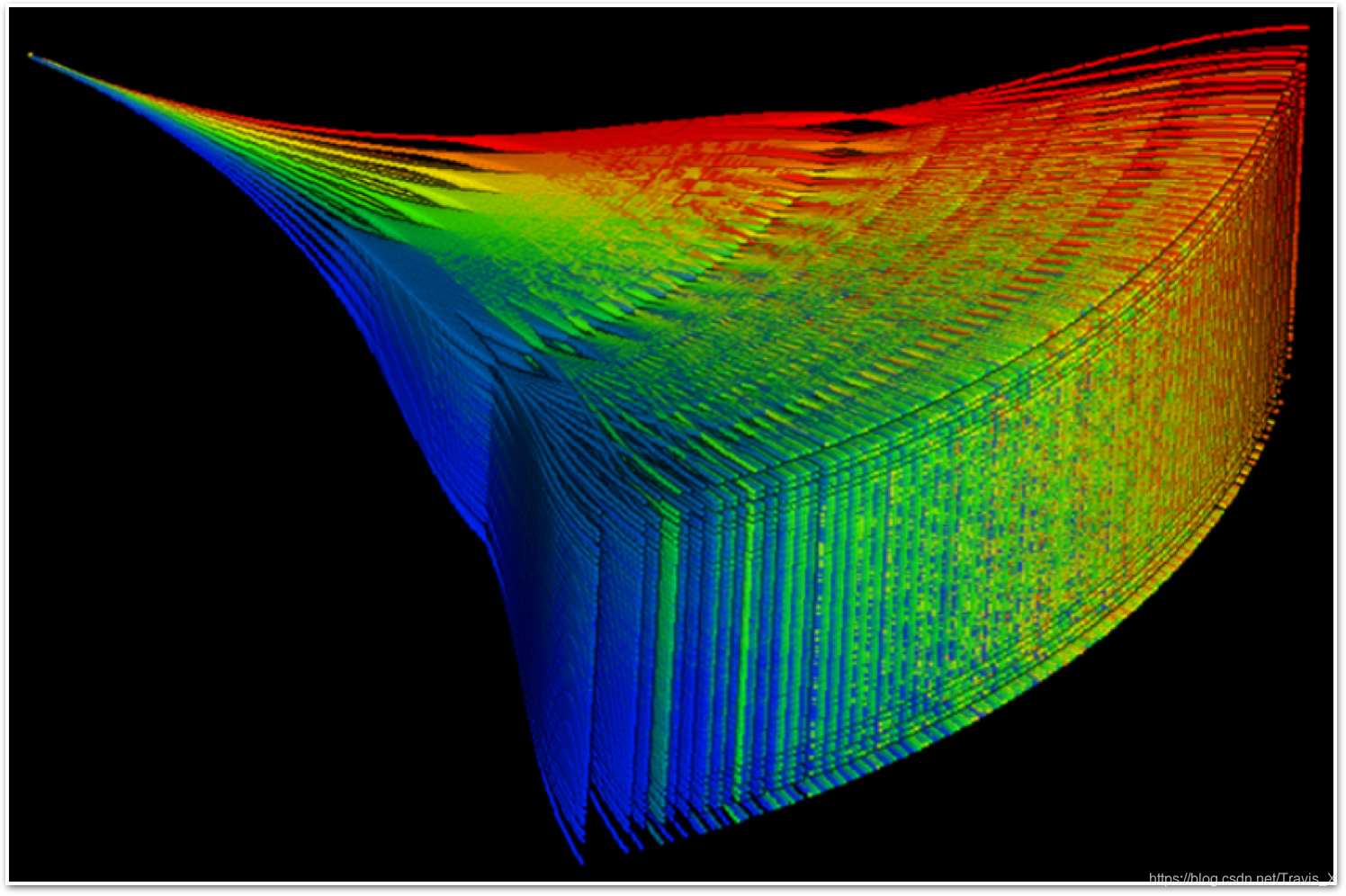
所有路径是根据车辆运动的约束生成的,组中的所有路径都可视为从 X s X_s Xs到 F F F的可行路径。 
可以将路径末端的状态视为 X f X_f Xf的样本 ξ i ξ_i ξi, i =1、2、…n ,其中的 X f X_f Xf分布是从 P ( X f ∣ X s ) P(X_f | X_s) P(Xf∣Xs)得出的。在导航过程中,障碍物会被传感器遮挡住某些路径。图中给出了一个障碍物示例以及组中相应的无碰撞路径。 定义一个布尔函数表示路径的间隙:

基于公式(4)可以计算出 P B ( X s ) P_B (X_s) PB(Xs):
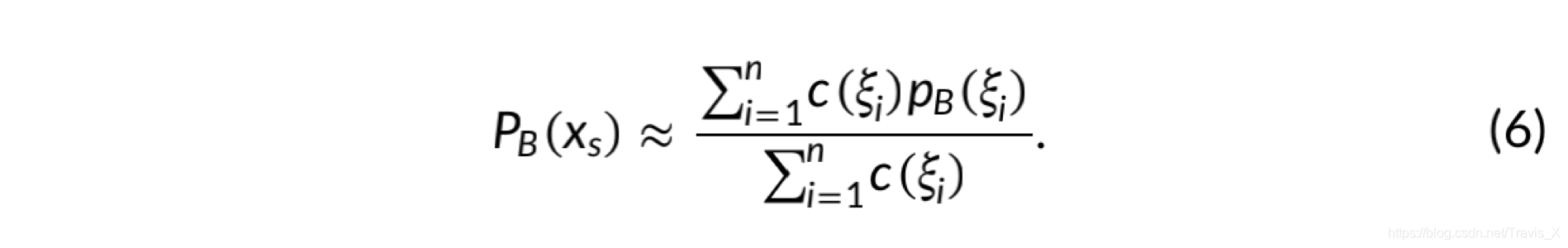
将公式(6)应用于所有的路径组,并选择最高 P B ( X s ) P_B (X_s) PB(Xs)的 X s ∗ X^*_s Xs∗来执行控制车辆。
4. 全局概率
环境是以体素网格来表示。与传统体素不同的是,我们的体素同时包含位置和方向信息。
如图(a)所示,基于恒定的角度间隔将体素分为多个方向,以 δ δ δ表示。角度间隔设置了车辆穿过体素的方向。 用 X j k , j , k X^k_j, j,k Xjk,j,k∈Z 表示体素的状态,其中 j j j是体素指数, k k k是方向指数。 与 X j k X^k_j Xjk相关的位置被建模在体素内,并且将该方向建模为围绕 X j k X^k_j Xjk方向均匀分布在[− δ / 2 δ / 2 δ/ 2δ/2 δ/2δ/2]内。 从 X j k X^k_j Xjk到达B的概率密度表示为 ρ B ( X j k ) \rho B(X^k_j) ρB(Xjk)。
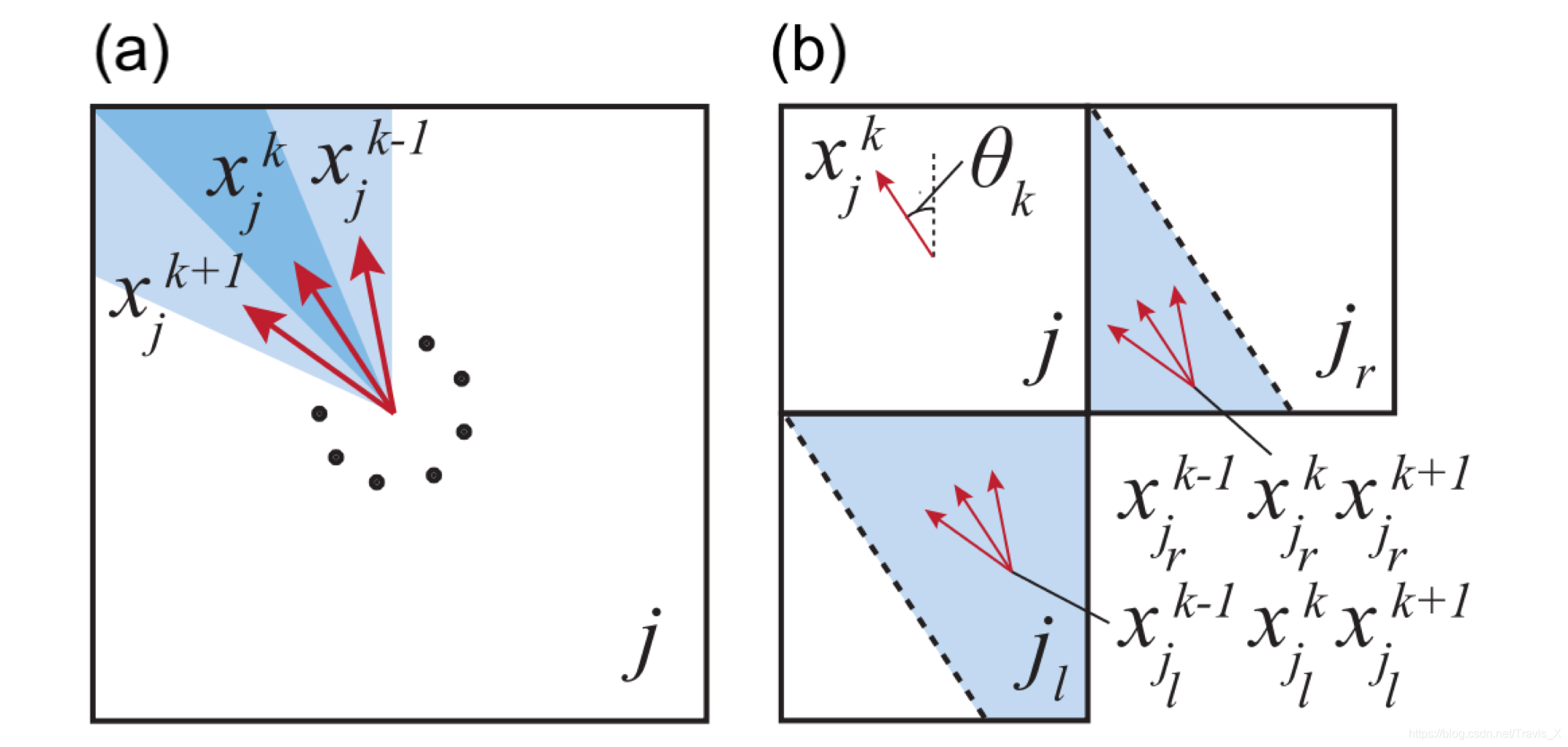
概率可在相邻体素之间传输。考虑概率是从相邻体素传输到 x j k x^k_j xjk的情况,在左下角表示为 j l j_l jl,在右上角表示为 j r j_r jr。 θ k θ_k θk为与 x j k x^k_j xjk相关的方向。由于位置被建模是均匀地分布在体素中,因此要传输到 x j k x^k_j xjk的概率来自体素 j l j_l jl和 j r j_r jr中的灰色区域,分别为体素的 1 − t a n θ k / 2 1 − tan θ_k/2 1−tanθk/2和 t a n θ k ∕ 2 tan θ_k∕2 tanθk∕2区域。 这里,灰色区域是通过在 j l j_l jl和 j r j_r jr中画一条平行于 x j k x^k_j xjk方向的线来确定的,该方向连接了体素j的左下和右上顶点。 从每个灰色区域,从三个相邻方向传输概率概率密度传输定义为:
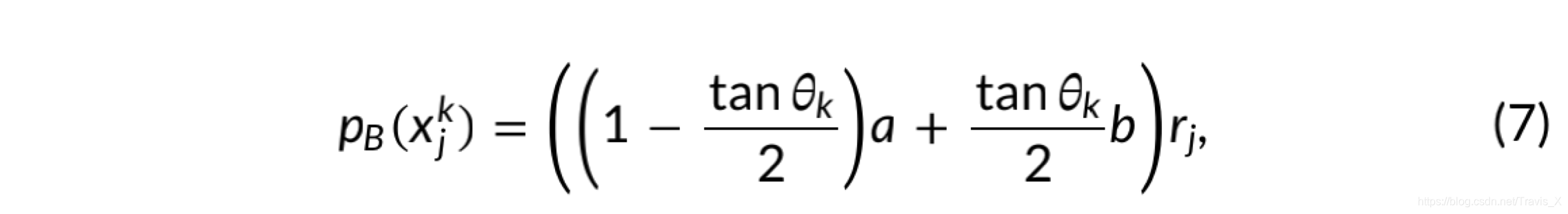
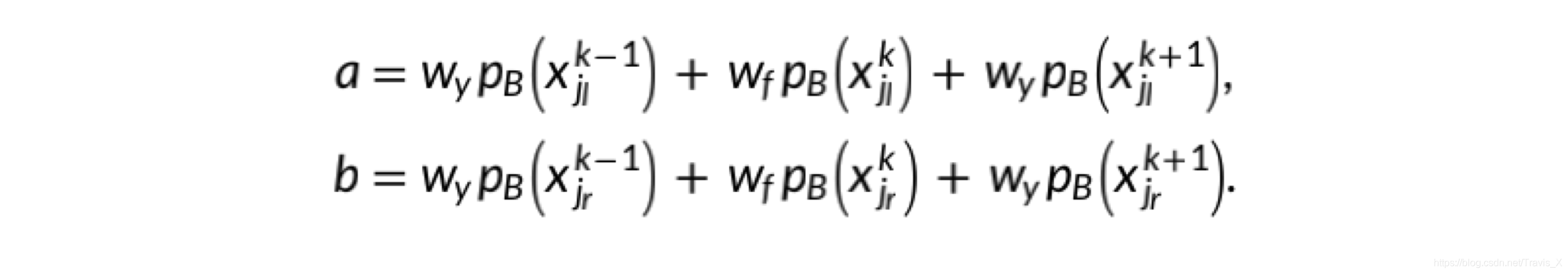
r j r_j rj表示由于障碍而引起的体素 j j j的可穿越性,其中 r j r_j rj = 1表示完全清除, r j r_j rj = 0表示完全闭塞。
w f w_f wf和 w y w_y wy分别确定对应于向后运动和偏航调整的概率分布。
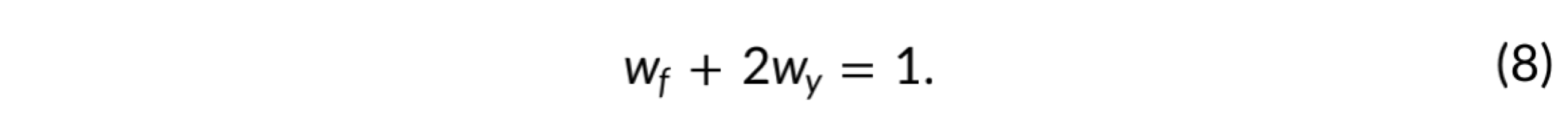
三维情况的扩展,与二维情况类似。
概率密度计算为:
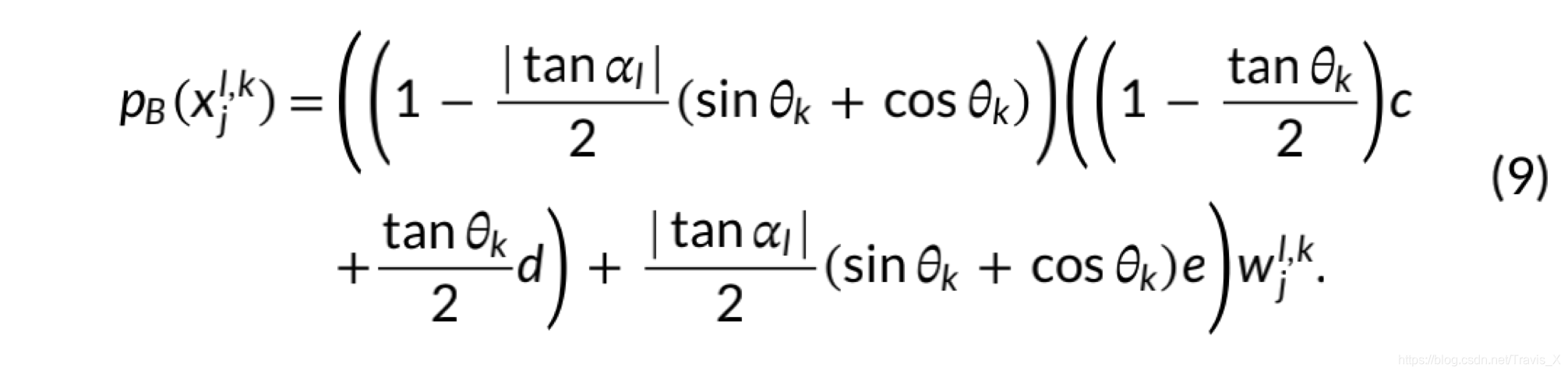
其中:
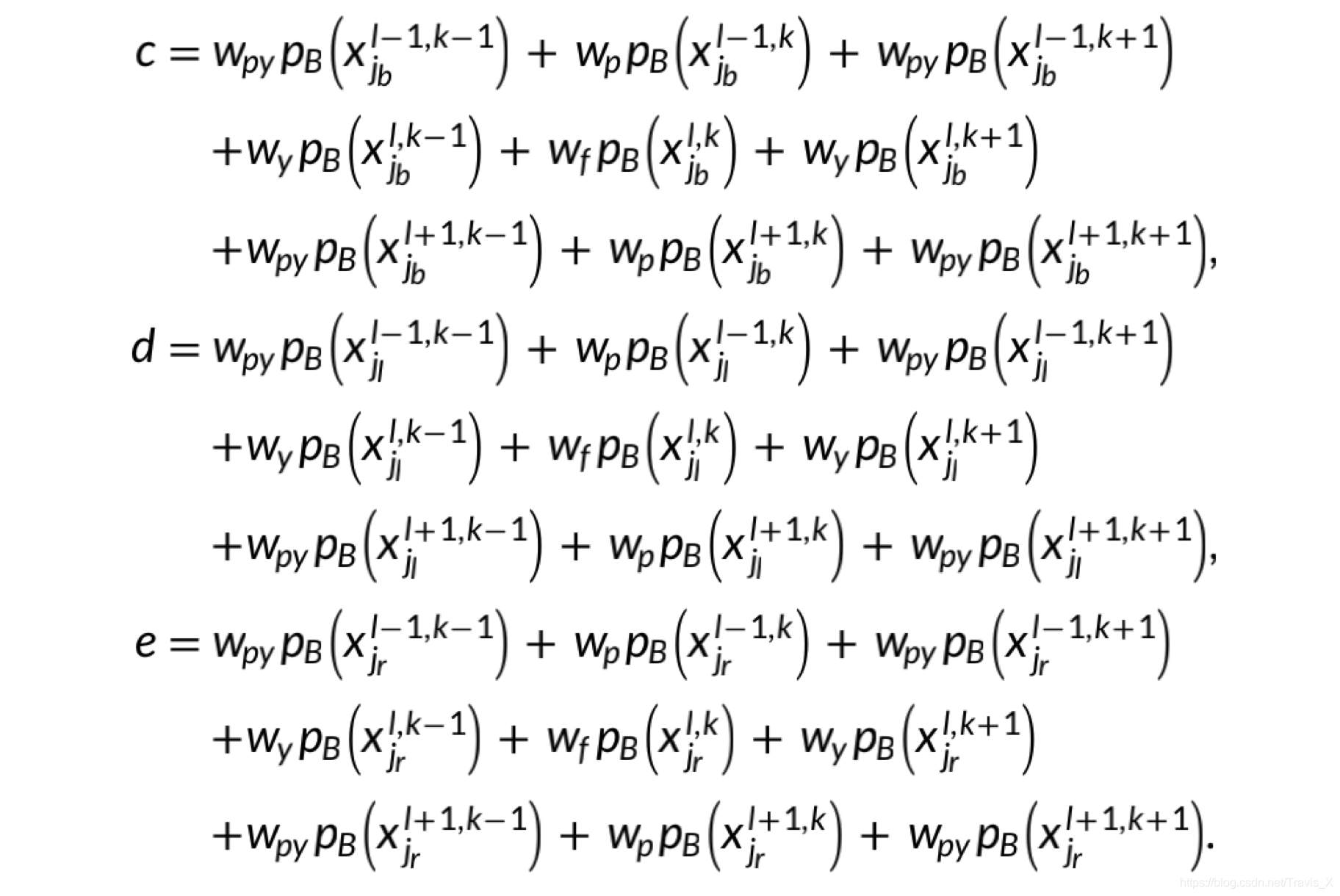
w j l , k w^{l,k}_j wjl,k表示 x j l , k x^{l,k}_j xjl,k障碍物的可遍历性。
w p w_p wp表示概率传输 ρ B ( x j ∗ l − 1 , k ) \rho_B(x^{l-1,k}_{j*}) ρB(xj∗l−1,k)和 ρ B ( x j ∗ l + 1 , k ) \rho_B(x^{l+1,k}_{j*}) ρB(xj∗l+1,k)到 ρ B ( x l , k ) \rho_B(x^{l,k}) ρB(xl,k)的转弯权重。
要求在传输过程中不损失任何概率:
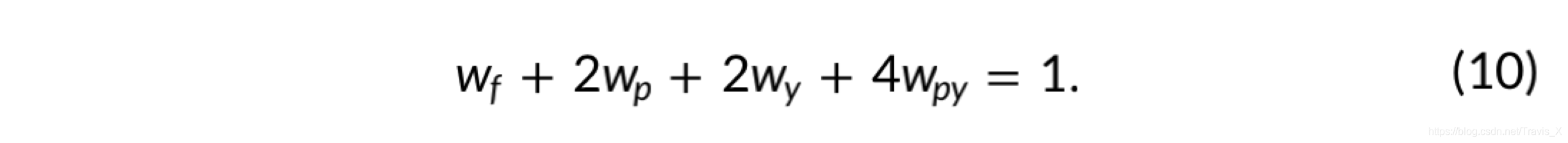
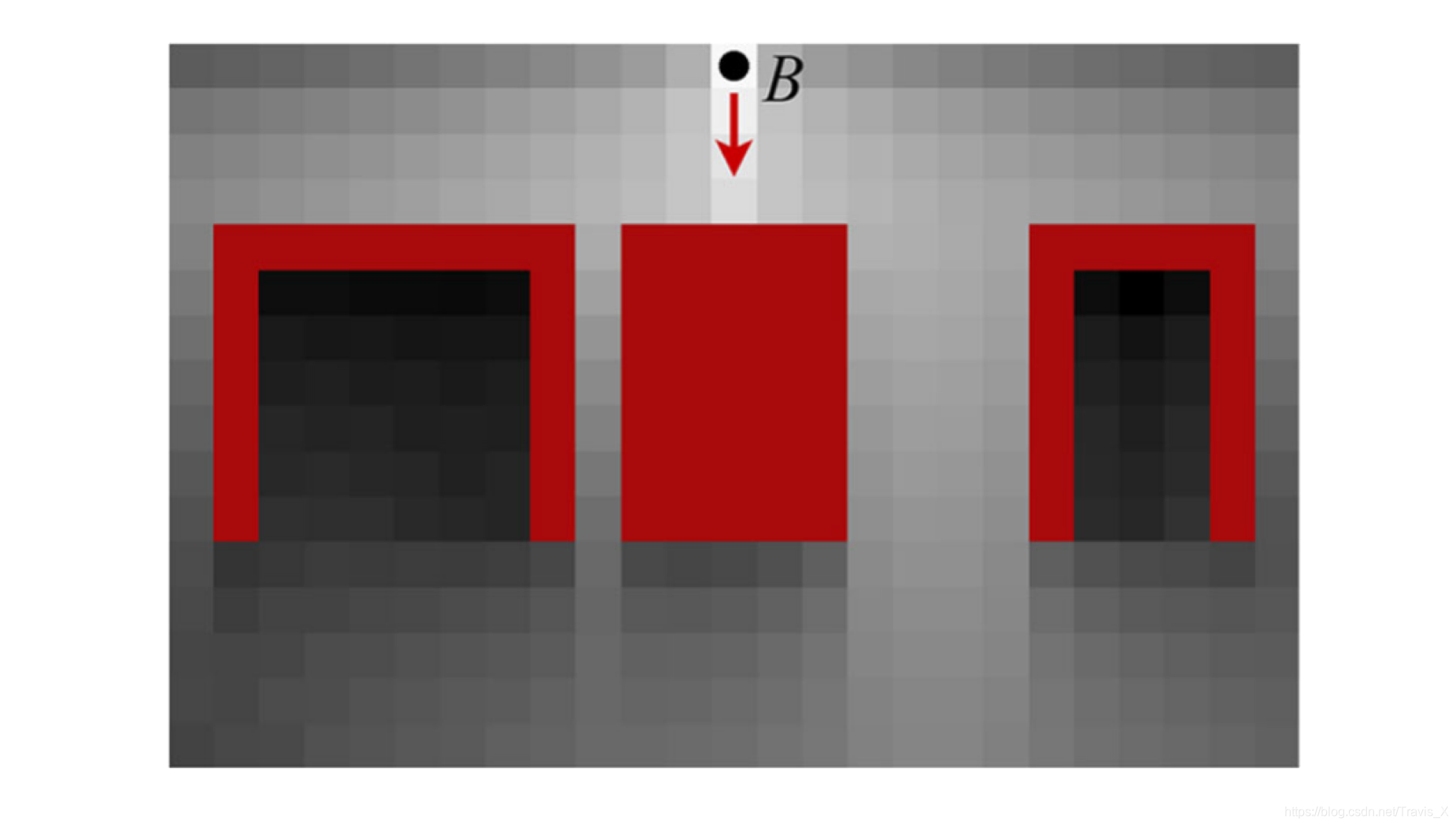
初始化期间,概率密度是均匀分布在包含B的体素中的所有方向上。概率的传播是通过迭代进行的。如图给出了2D环境中传播的概率密度演示。体素越亮表示概率密度越高。
5. 方法实现
路径组是离线生成的。我们使用传感器覆盖范围 S S S生成体素网格来做碰撞检测。
体素和路径之间的对应关系是预先建立,并存储在邻接表中。在邻接表中,每一行都与一个体素相关联,并由路径的索引组成,这些路径被放置在体素中心的障碍物所遮挡。接着,要考虑车辆半径来计算遮挡。
系统启动后,路径和邻接表将加载到机载电脑中。在线碰撞检测会处理所有感知数据,并根据邻接表标记要遮挡的相应路径。然后,该算法会遍历每组中的所有路径,并基于(6)计来算 P B ( X s ) P_B (X_s) PB(Xs),并选择最高 P B ( X s ) P_B (X_s) PB(Xs)值的路径组。 该算法返回 x ∗ s x^s_* x∗s:

三、项目演示
差速机器人模型的仿真
[运动规划算法]基于似然场的快速避障算法(1)
加入A*算法作全局规划
[运动规划算法]基于似然场的快速避障算法(2)
参考
【1】Ji Zhang Chen Hu Rushat Gupta Chadha Sanjiv Singh,Falco: Fast likelihood‐based collision avoidance with extension to human‐guided navigation.
这篇关于[运动规划算法]基于似然场的快速避障算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




