BST AVL RBT

本文主要是介绍BST AVL RBT，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

BST

定义

• 根节点的值大于左子树包含的节点的值
• 根节点的值小于右子树包含的节点的值
• 左右子树都是BST

插入

假设当前节点为 cur ，待插入节点为 node ，根节点为 root ，分如下四种情况：

1. root == None: root=node
2. cur.val == node.val: 不做任何处理
3. cur.val > node.val:
   • if cur.left == None: cur.left = node
   • if cur.left != None: 递归左子树
4. cur.val < node.val:
   • if cur.right == None: cur.right = node
   • if cur.right != None: 递归右子树

删除

分如下三种情况：

1. 删除节点为叶子节点：直接删除
2. 删除节点只有一个子节点：删除节点的父节点指向其唯一的那个子节点
3. 删除节点有两个子节点：选择后继节点（右子树的最小节点）来顶替其位置，然后删除后继节点

AVL

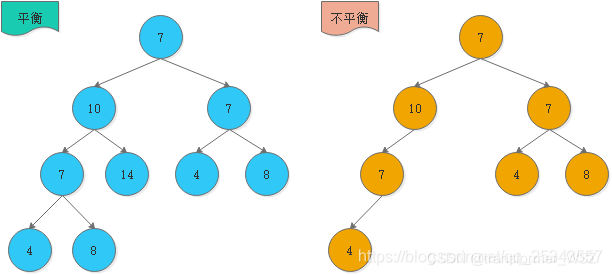
平衡因子：树中某结点其左子树的高度和右子树的高度之差

定义

• 特殊的BST，树中任意一个节点的平衡因子绝对值小于等于1

AVL的插入和删除时间复杂度均为 $O(lo{g}_{2}n)$ ，$n$ 为树中节点个数。

AVL树大部分操作都和BST树相同, 只有在插入删除结点时, 有可能造成AVL树失去平衡, 而且只有那些在被插入/删除结点到根节点的路径上的结点有可能出现失衡, 因为只有那些结点的子树结构发生了变化。

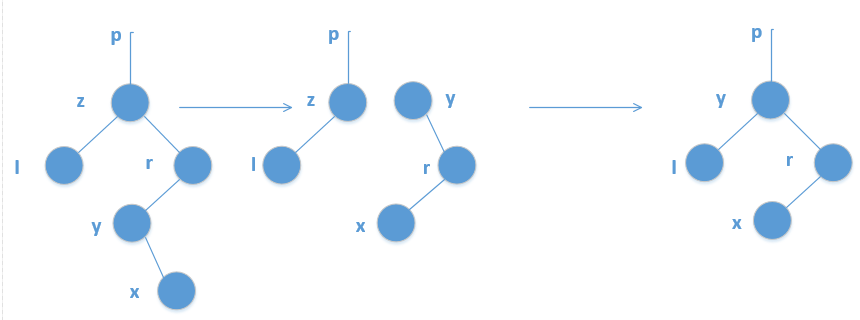
这时我们需要一些操作来把树恢复平衡，这些操作叫做AVL树的旋转：

• LL
• RR
• LR
• RL

具体操作可见 平衡二叉树(AVL树)的平衡原理以及插入,删除操作 和 AVL树的插入和删除

插入

• 当插入新结点导致不平衡时, 我们需要找到距离新节点最近的不平衡结点为轴来转动AVL树来达到平衡

删除

• AVL删除节点的操作与和BST一样, 不同的是删除一个结点有可能引起父结点失衡。与插入不同，除了在父节点处旋转外，可能必须在父节点的祖先处再进行旋转。因此，我们必须继续追踪路径，直到到达根为止。

RBT

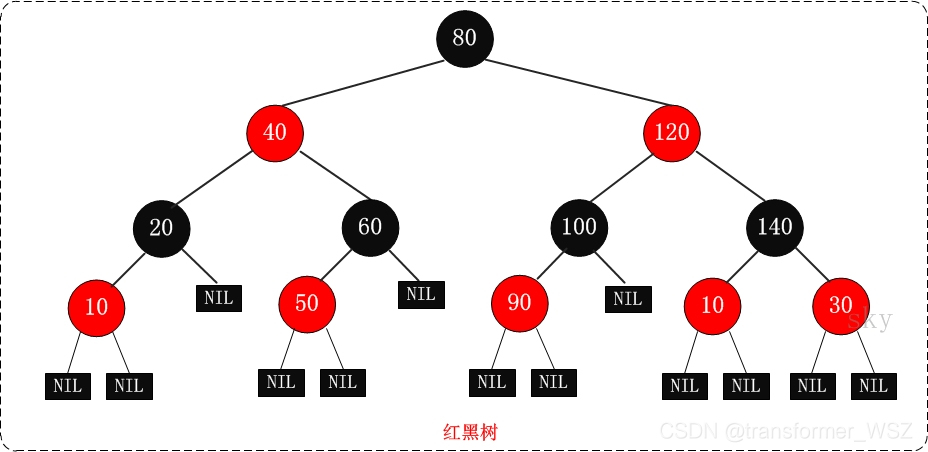
• 一棵含有 $n$ 个节点的红黑树的高度至多为 $2log(n+1)$
• RBT的插入和删除时间复杂度均为 $O(lo{g}_{2}n)$ ，$n$ 为树中节点个数

定义

RBT也是一种特殊的BST，此外它还有如下五个特性：

1. 每个节点要么黑色，要么红色
2. 根节点为黑色
3. 每个叶子节点为黑色（这里叶子节点专指值为None的节点）
4. 如果一个节点为红色，那么它的子节点必为黑色
5. 任意一节点到每个叶子节点的路径上都包含相同数量的黑色节点

插入、删除

RBT的插入和删除情况较为复杂，具体案例可见 什么是红黑树？面试必问！ 和 红黑树(一)之 原理和算法详细介绍

RBT相比于BST、AVL有什么优缺点

• RBT是牺牲了严格的高度平衡的优越条件为代价，它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能。红黑树能够以 $O(lo{g}_{2}n)$ 的时间复杂度进行搜索、插入、删除操作。此外，由于它的设计，任何不平衡都会在三次旋转之内解决。当然，还有一些更好的，但实现起来更复杂的数据结构能够做到一步旋转之内达到平衡，但红黑树能够给我们一个比较“便宜”的解决方案。

• 相比于BST，因为红黑树可以能确保树的最长路径不大于两倍的最短路径的长度，所以可以看出它的查找效果是有最低保证的。在最坏的情况下也可以保证 $O(logn)$ 的，这是要好于二叉查找树的。因为二叉查找树最坏情况可以让查找达到 $O(n)$ 。

• RBT的算法时间复杂度和AVL相同，但统计性能比AVL更高。AVL在插入和删除中所做的后期维护操作会比RBT要耗时好多，但是他们的查找效率都是 $O(logn)$ ，所以RBT应用还是高于AVL的。实际上插入AVL和RBT的速度取决于你所插入的数据。如果你的数据分布较好,则比较宜于采用AVL(例如随机产生系列数)，但是如果你想处理比较杂乱的情况，则RBT是比较快的。

---

参考自

• BST（二叉搜索树）
• 平衡二叉树(AVL树)的平衡原理以及插入,删除操作
• 详细图文——AVL树
• AVL树的插入和删除
• 什么是红黑树？面试必问！
• 红黑树(一)之 原理和算法详细介绍
• 面试题——轻松搞定面试中的红黑树问题

这篇关于BST AVL RBT的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---