物理学视角讲解diffusion生成模型——数学基础和一维度实现

本文主要是介绍物理学视角讲解diffusion生成模型——数学基础和一维度实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

从物理学的视角来看扩散过程模型。之所以整理这个系列是因为现在大部份讲生成模型的教程都是直接从加噪、去噪、然后代码实现角度来讲。然而为什么要这么加噪、去噪、为什么要高斯拟合，如果我不这么做会怎么样，后续我要优化我的代码要从那下手呢。这些原理层面的东西基本没有讲，这就相当于给了一套生产流程，我们并不知道这套流程是怎么设计背后思想是什么。我们后续碰到问题如果要升级改造这个流程和链路要从何下手呢。要怎么接续上这套流程的设计思路呢。
所以这个系列就是从这个视角切入，来讲解物理学家视角的扩散过程。以及当时为什么选择了扩散过程来作为生成模型的一个框架，并且给出了这些框架的考量指标。同时会带你从1维、2维、3维做扩展，带你经历从理论到现在工业模型进阶。
这个系列文章包括一下几部份：
1.SDE数学基础
2.扩散模型选择的考量
3.几种可行的扩散模型
4.一维扩散模型实现
5.二维高斯扩散模型实现
6.条件扩散模型
7.latent扩散模型
8.扩散模型的几大类求解器
9.工业实现例子拆解
开始之前我们先来看看物理学家或者数学家是怎么思考和解决问题的。他们有什么思维的范式。如果要总结那其实就是三句话：1.观察现象抽取范式 2.提出系列标准，构建解决问题框架 3.推广具象求解，具体步骤列入下：
1.现象观察
2.抽取影响因素
3.建立规则模型表达
4.有几种表现形式
5.有几种经典范例
6.每种范例特性表达形式如何
7.如何求解
8.选择合适范例做好约束解决问题

数学基础知识

扩散方程通常被称为菲克第二定律，它在数学上表示了我们观察到的墨水等物质随时间扩散或扩散的过程。从本质上讲，它的定义是：
$\frac{\partial \phi}{\partial t} = D \nabla^2 \phi$
phi：是物质的浓度。它象征着我们物质的浓度，就像特定水域中墨水的密度一样。
t：代表时间。
∂phi/∂t：这个速率分量告诉我们这个浓度如何随着时间的推移而变化。这就像观察墨水在水中扩散的速度有多快。
D：称为扩散系数，该系数体现了我们物质固有的“扩散速度”。这就是为什么有些物质消散得很快，而另一些物质则需要很长时间的原因。
∇²phi: 称为拉普拉斯算子，表示空间二阶导数。
方程的这一部分让我们深入了解物质传播的方向和程度。这类似于确定我们的墨水想要行进的方向以及它想要分散的程度。
出于计算目的，连续扩散方程通常是离散的，允许其在迭代深度学习框架中应用。这涉及将时间和空间分解为离散的步骤和单元。
离散化如何工作？
离散化扩散方程意味着将我们对时间和空间的连续视图转换成小的、不同的块，类似于将平滑渐变转换成一组单独的色块。对于计算模型，比如深度学习中的模型，这种逐步的视角至关重要。
现在，对于扩散方程：
$\frac{\partial \phi}{\partial t} = D \nabla^2 \phi$
当我们对其进行离散化时，我们可以使用离散步骤来表示浓度、时间和空间的变化：
让我们使用：
Δt 表示离散时间步长。
Δx 用于 x 方向上的离散空间步长（对于 y、z，如果是 2D 或 3D，则类似）。
我们的离散扩散方程可以看起来像这样：
$\phi(x,t+\Delta t）- \phi(x,t) = D[\phi(x+\Delta x,t) - 2 \phi(x,t) + \phi(x-\Delta x,t)]\frac{1}{\Delta x^2}$
该方程本质上表明，小时间步长 (Δt) 内任何点的浓度变化取决于当前时间相邻点之间的浓度差（由 Δx 确定）。
扩散方程和生成建模之间的联系：
扩散作为生成过程：在深度学习中，扩散方程可以用来描述生成过程。这个想法是将数据分布视为随时间扩散的“物质”。该过程从简单分布开始，通过迭代步骤接近目标复杂分布。
噪声添加和迭代细化：通过添加噪声，我们将数据推向更简单的分布。由神经网络促进的迭代细化试图扭转这一过程。这类似于在每一步对数据进行“去噪”，逐渐使其更接近目标分布。
概率解释：扩散过程可以用概率来看待。在每一步中，给定当前状态，下一个状态都有一个概率分布。扩散模型中的神经网络经过训练来捕获这种转移概率，从而帮助生成过程。

动态系统是一个发生运动的系统；其中的组件或变量随时间演变。假设有一个动态系统，在这个系统中，变量 y 随时间 t 被观察。此外，存在一个未被观察到的隐藏状态 x，它控制着 y 随时间的演变。因此，使用贝叶斯定理，该模型被描述为
$p(x_t | y_t) ∝ p(y_t | x_t) p(x_t)，$
其中 y 通过观测模型被观测到。如果是高斯分布，观测模型可以写作：
$p(y_t | x_t) ∼ N(y_t | Hx_t, R)$ ,
其中 t ∈ [0, T]。此外，为了进行推断，需要对 x 引入一个先验。对于动态建模，微分方程成为先验的自然选择。由于随机微分方程（SDEs）相对于常微分方程（ODEs）的稳健性，更倾向于使用 SDEs。然而，在讨论具有 SDE 先验的模型之前，先简要讨论一下 SDEs。

随机微分方程（SDE）
微分方程是关系函数及其导数的方程，应用范围涵盖物理、化学和经济等领域。任何系统的动态都可以用一个控制系统状态随时间变化的微分方程来表达：
$\frac{dx(t)}{d_t} = f(x(t), t)$
其中 x(t) 是时间 t 时系统的状态，f(.) 是控制函数。这被称为常微分方程（ODE）。
给定初始值，方程的解为：
$\int_{t=0}^{T} f(x(t), t) dt$
这通常被称为初始值问题（IVP）。用于解决IVP的一种数值方法是欧拉方法
$X (t + h) = X (t) + f (X (t), t) h$
其中 h 是时间步长。
例如：
考虑一个弹簧-质量模型
$d^2x(t)/dt^2 + γ dx(t)/dt + v^2x(t) = w(t)$
在状态空间形式中，它被写为：
$f(X(t), t) = [0 1; -v^2 -γ] X(t) + [0; 1] w(t)$
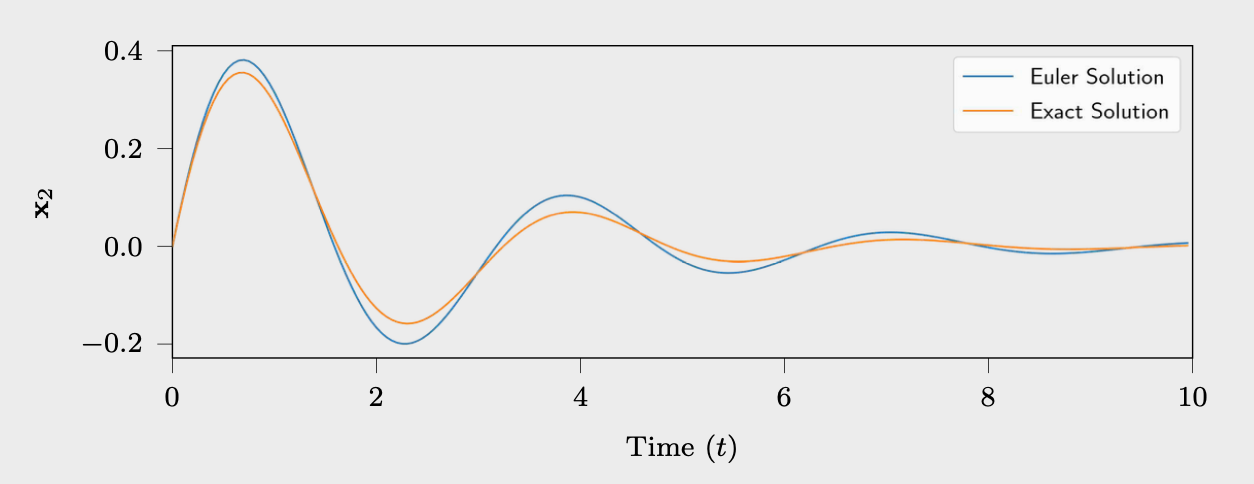
欧拉方法解决弹簧-质量初始值问题（IVP）模型及其与真实解的比较
在这里， $\frac{dX(t)}{dt} 而 X(t) = \begin{bmatrix} x(t) \\ \frac{dx(t)}{dt} \end{bmatrix}$ 。设定参数 $\gamma = 1 ，且 w(t) = 0$ 。使用欧拉方法模拟的轨迹，时间 t 在 [0,10] 范围内，步长为 0.05，初始位置 $x_0 = [0, 1]$ 。
与常微分方程（ODEs）相关的一个缺点是，它没有包括可能存在于系统/环境/传感器中的不确定性。一种合理的包含这些不确定性的方法是添加高斯噪声：
$\frac{dx(t)}{dt} = F(x(t), t) + \epsilon,$
其中 $\epsilon \sim N(0, I)$ 。在方程中，噪声的强度是恒定的，可以通过引入一个新函数 $L(\cdot)$ 来使其变为可变的：
$\frac{dx(t)}{dt} = F(x(t), t) + L(x(t), t) \epsilon.$
的一个问题是，由于高斯白噪声的不连续性，它不是全局可微分的。为了缓解这个问题，引入了伊藤积分，这导致了下面的方程，使用布朗运动：
$d\beta(t)$
其中 $F (x (t), t)$ 被称为漂移函数， $L (x (t), t)$ 为扩散函数，而 $d\beta(t)$ 是具有谱密度Q的布朗运动。
解决随机微分方程（SDE），即方程的一个常用数值方法是欧拉-丸山方法：
$x_{t+h} = x_t + F(x_t, t) h + \sqrt{h} L(x_t, t) \omega(t),$
其中 $\omega(t) \sim N(0, Q)$ 且 h 是时间步长。
示例：
在方程中，如果将驱动力视为高斯噪声，该方程可写为
$\begin{bmatrix} 0 & 1 \\ -v^2 & -\gamma \end{bmatrix} X(t) + \begin{bmatrix} 0 \\ \epsilon(t) \end{bmatrix},$
其中 $\epsilon(t) \sim N(0, Q)$ 。现在，使用与前一个示例相同的值，并且 Q = 0.005 I ，通过欧拉-丸山方法模拟的轨迹如图所示。
100条欧拉-丸山方法解决的弹簧-质量初始值问题（IVP）模型的轨迹，包括高斯噪声和平均轨迹
与常微分方程（ODE）的确定性解相比，随机微分方程（SDE）提供了随机解（轨迹）。因此，SDE相对于ODE的一个主要优势是其稳健性和量化不确定性的能力。

SDE 先验

具有高斯观测模型的动态系统可以表示为
$p(x_t | y_t) \propto p(y_t | x_t) p(x_t), \\ \quad p(y_t | x_t) \sim N(Hx_t, R).$
此外，为了学习动态，引入了关于 x 的 SDE 先验：
$d\beta(t).$
使用 SDE 先验的一个假设是系统是马尔可夫的。所谓马尔可夫，是指在任何时间 t，给定全部过去的未来事件的条件概率与给定时间 t 的状态的该未来事件的条件概率相同。
为了进行推断，即计算后验，可以使用近似推断方法。如 Särkkä & Solin所讨论的，具有线性漂移函数的 SDE 与高斯过程（GPs）有关系。因此，在假设线性 SDE 并使用马尔可夫性质的情况下，可以使用马尔可夫 GPs 作为近似分布族进行变分推断（VI）。

状态空间模型

状态空间模型（SSM）是一种建模方法，其中动态系统的状态表示为一组一阶微分或差分方程。系统的状态定义为完全描述系统的最小变量集，即它包含足够的信息来预测未来的状态/行为。
示例：
考虑一个线性时变动态模型，其中 $\in \mathbb{R}^n$ 是状态向量， $\in \mathbb{R}^m$ 是观测向量，x的速度表示为 $\dot{x}(t)$ 。然后，状态空间模型方程写为
$\dot{x}(t) = A(t) x(t) + B(t) u(t), \\ \quad y(t) = C(t) x(t) + D(t) u(t),$
其中 $\in \mathbb{R}^n$ 是状态向量, $\in \mathbb{R}^m$ 是观测向量， $\in \mathbb{R}^p$ 是控制向量， $\in \mathbb{R}^{n \times n}$ 是系统矩阵， $\in \mathbb{R}^{n \times p}$ 是输入矩阵， $\in \mathbb{R}^{m \times n}$ 是输出矩阵， $\in \mathbb{R}^{m \times p}$ 是反馈矩阵。
状态空间模型适用于连续时间和离散时间模型，以及时变和时不变模型。SSM的一个主要优点是系统的紧凑和简洁的表示，有助于快速和有效的分析。

马尔可夫高斯过程

高斯过程（GP）（Rasmussen & Williams, 2006）是一个关于函数的分布。形式上，高斯过程被定义为在输入空间 $\mathbb{R}^d$ 上的一个随机函数 f(x)，由均值函数 $\mu(x)$ 和协方差函数 $\kappa(x, x')$ 特征化。函数 f(x)上的 GP 先验表示为
$\sim GP(\mu(x), \kappa(x, x')),$
其中 $\mu(x) = E[f(x)] 和 \kappa(x, x') = \text{Cov}(f(x), f(x'))$ 。
如所讨论的，马尔可夫过程具有 $x_{n+1}$ 的分布条件依赖于 $\{x_0, x_1, \ldots, x_n\}$ 与仅依赖于 $x_n$ 的分布条件相同。
因此，如果一个随机过程同时遵循高斯过程和马尔可夫过程的属性，则该过程是一个马尔可夫高斯过程。

稀疏变分高斯过程

高斯过程（GP）模型的一个主要限制是计算复杂性，因为它涉及到逆转一个 $\mathbb{R}^{n \times n}$ 矩阵，这是一个 $O(n^3)$ 的操作。因此，它对数据的扩展性很差。
最近，研究在这方面取得了进展，其中最著名的工作之一是稀疏变分高斯过程（SVGP）（Hensman等，2015b），它使用变分近似。它使用 m 个引导点而不是实际的 n 个数据点；引导点不一定是数据点，并且随时间学习。它将计算复杂性降低到 $O(m^3)$ 。增强模型与引导点一起写为 $p (y, f, u) = p (y ∣ f) p (f ∣ u) p (u)$ 。
变分推断（VI）用于通过 $q (f, u)$ 近似后验 $p (f, u ∣ y)$ ，并选择分布族 Q 的形式为 $q (f, u) = p (f ∣ u) q (u)$ ，其中 $\sim N(m, S)$ 。
可以使用詹森不等式计算ELBO，如下：
$\log p(y) \geq \mathbb{E}_{q(u, f)} [\log p(y | f)] - \mathbb{E}_{q(u, f)} \left[\frac{\log q(f, u)}{p(f, u)}\right] \geq \mathbb{E}_{q(f)} [\log p(y | f)] - D_{KL} [q(u) \| p(u)].$
示例：
有一组200个数据点，目标是在此数据上条件化一个GP模型。然而，由于经典GP模型的高复杂性，使用带有20个可学习引导点的SVGP。
使用Adam优化器（Kingma & Ba, 2015）对ELBO进行了40个时代的优化，学习率为0.05。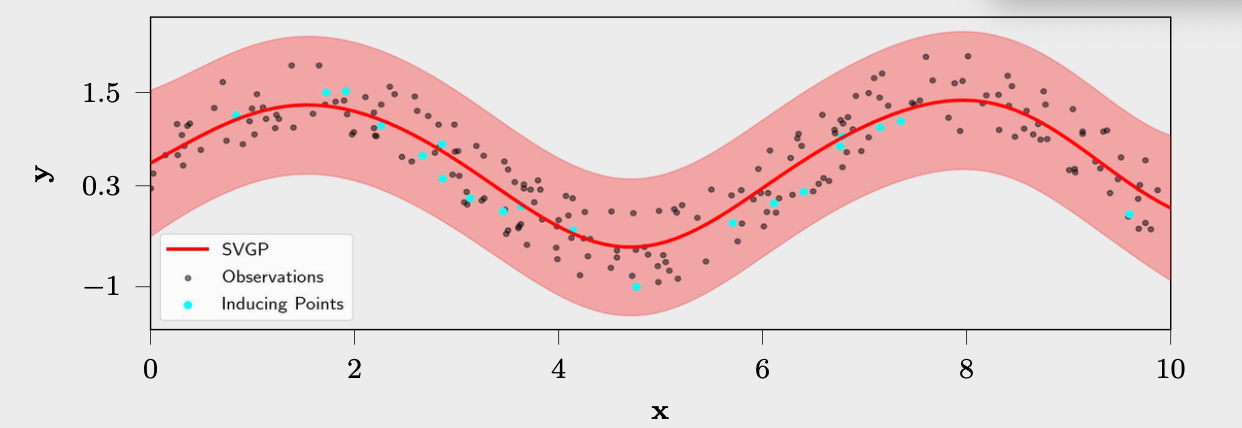
SVGP模型后验的均值和95%置信区间，以及学习到的引导点（青色）和数据点（黑色）

双重稀疏变分高斯过程

Adam等人（2020）研究了结合SSM和SVGP的优势以解决GP中的计算复杂性问题。他们将跨域引导特征的思想与状态空间GP公式结合起来，称之为双重稀疏变分高斯过程（S2VGP）。用于引导特征的线性算子 $\psi$ 被选择为
$\psi_i : f \rightarrow s(z_i) = [f(z_i),...,f^{(d-1)}(z_i)]^\top,$
其中 $[z_1, \ldots, z_m]$ 是有序的引导点， $s (\cdot)$ 表示状态。
这导致引导状态 $\{\psi_i[f_Q]\}_{i=1}^M$ 是马尔可夫的，并遵循高斯分布，即 $p_\psi(U) = p(u_1) \prod_{i=1}^{M-1} p(u_{i+1} | u_i)$ 。
另一个有趣的属性是，函数的后验仅依赖于最近的右侧和左侧引导点， $p(f(x_n) | u) = p(f(x_n) | u_{n-}, u_{n+})$ 。
S2VGP的ELBO定义为
$\sum_{n=1}^N \left[ \mathbb{E}_q[\log p(y_n | f(x_n))] - \frac{1}{2} \text{tr}(Q_\psi \Sigma_{uu}) + \frac{1}{2} |\Sigma_{uu}| + c(\mu_u, p_\psi) \right].$
有关更多详情，请参阅Adam等人（2020）。

一维扩散模型

一维扩散过程（在实数线上）可以通过随机微分方程来定义。
$\dot{x} = \sigma \ \eta(t)$
其中σ>0是一个常数，而η(t)表示高斯白噪声项。
这到底是什么意思？我们可以通过定义上述表达式为离散过程的小Δt极限来使其具体化。
$\Delta t) = x(t) + \sigma \sqrt{\Delta t} \ r$
其中r∼N(0,1)是来自标准正态分布的一个样本。这是一个欧拉-马鲁亚马时间步的例子。
上述扩散的描述对于进行模拟很有用。给定一个数字x，我们可以使用上述更新规则使其经历一个时间步的扩散。但是，一个补充的视角描述了概率密度p(x,t)，系统在时间t处于位置x的概率，随时间如何变化。特别是，p(x,t)根据著名的扩散方程进行变化：
$\frac{\partial p(x, t)}{\partial t} = \frac{\sigma^2}{2} \frac{\partial^2 p(x, t)}{\partial x^2} \ .$
你可能习惯于看到这个方程使用扩散常数D而不是参数σ。它们之间的转换是D:=σ²/2。
扩散方程的解，在给定一个δ函数作为初始条件p(x,0)=δ(x-x₀)（即，假设我们最初确定系统位于位置x₀）的情况下，是众所周知的热核：
$x_0, 0) = \frac{1}{\sqrt{2 \pi \sigma^2 t}} \exp\left\{ - \frac{(x - x_0)^2}{2 \sigma^2 t} \right\} \ .$

给定一个任意的初始条件p(x,0)=p₀(x)，扩散方程的一般解随后是
$\int_{-\infty}^{\infty} p(x, t | x_0, 0) p_0(x_0) \ dx_0 \ .$

随机微分方程（SDEs）基础

扩散只是受随机微分方程（SDE）控制的随机过程中一个特别简单的例子。最通用的一维SDE形式如下：
$\dot{x} = f(x, t) + g(x, t) \ \eta(t)$
其中f(x,t)和g(x,t)是函数，η(t)再次是一个高斯白噪声项。函数f(x,t)是漂移项，描述了x(t)的平均值如何随时间演变。涉及g(x,t)的项是噪声或扩散项，描述了x(t)值的随机波动。
这到底是什么意思？不同于扩散的情况，其中g(x,t)是一个常数，在使上述表达式明确定义方面有额外的数学细节。对我们而言，我们可以选择被称为伊藤解释的约定，它定义了上述表达式为离散过程的小Δt极限。
$\Delta t) = x(t) + f(x(t), t) \Delta t + g(x, t) \sqrt{\Delta t} \ r$
其中r∼N(0,1)是来自标准正态分布的一个样本。这是一个更通用的欧拉-马鲁亚马时间步（尽管这仍然不是最通用的形式，因为我们目前只在一维中工作）。
与扩散方程相对应的是福克-普朗克方程（FPE），它描述了一个由随机微分方程（SDE）描述的系统中p(x,t)如何随时间演变。对于上述用伊藤解释写成的一维系统，它是由以下给出的
$\frac{\partial p(x, t)}{\partial t} = - \frac{\partial}{\partial x} \left[ \ f(x, t) p(x, t) \ \right] + \frac{\partial^2}{\partial x^2} \left[ \ \frac{g(x, t)^2}{2} p(x, t) \ \right] \ .$

大多数FPE都难以或无法通过解析方法解决，因此我们可能无法得到p(x,t)的精确解。我们能够精确求解p(x,t)的著名情况包括扩散和类Ornstein-Uhlenbeck过程（OU过程）。OU过程是均值回归的随机过程；一个一维的例子是SDE
$\dot{x} = \frac{1}{\tau} \left[ \mu - x \right] + \sigma \sqrt{\frac{2}{\tau}} \ \eta(t) \ .$
其解（对于初始条件p(x,0)=δ(x-x₀)）是
$x_0, 0) = \frac{1}{\sqrt{2 \pi s(t)^2}} \exp\left\{ - \frac{[ x - \mu(t) ]^2}{2 s(t)^2} \right\}$
其中
$KaTeX parse error: {split} can be used only in display mode.$
在长时间极限（t→∞）下，我们有
$x_0, 0) \xrightarrow{t \to \infty} p_{ss}(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left\{ - \frac{(x - \mu)^2}{2 \sigma^2} \right\} \ ,$

即稳态解 $p_{ss}(x)$ 是一个均值为μ和方差为σ²的高斯分布。
这个OU过程的一般解（给定一个初始分布p(x,0)=p₀(x)）是
$\int_{-\infty}^{\infty} p(x, t | x_0, 0) p_0(x_0) \ dx_0 \ .$
OU过程与严格的扩散过程有些不同的一点是，它们的长时间行为会完全丧失对初始条件的记忆。也就是说，随着t的增加，p(x,t)越来越不依赖于p₀(x)。

基础示例代码

让我们看看模拟一维扩散过程可能是什么样子，这是一个特别简单的随机过程。你也可以自己动手修改代码，来模拟其他的随机微分方程，比如奥恩斯坦-乌伦贝克过程。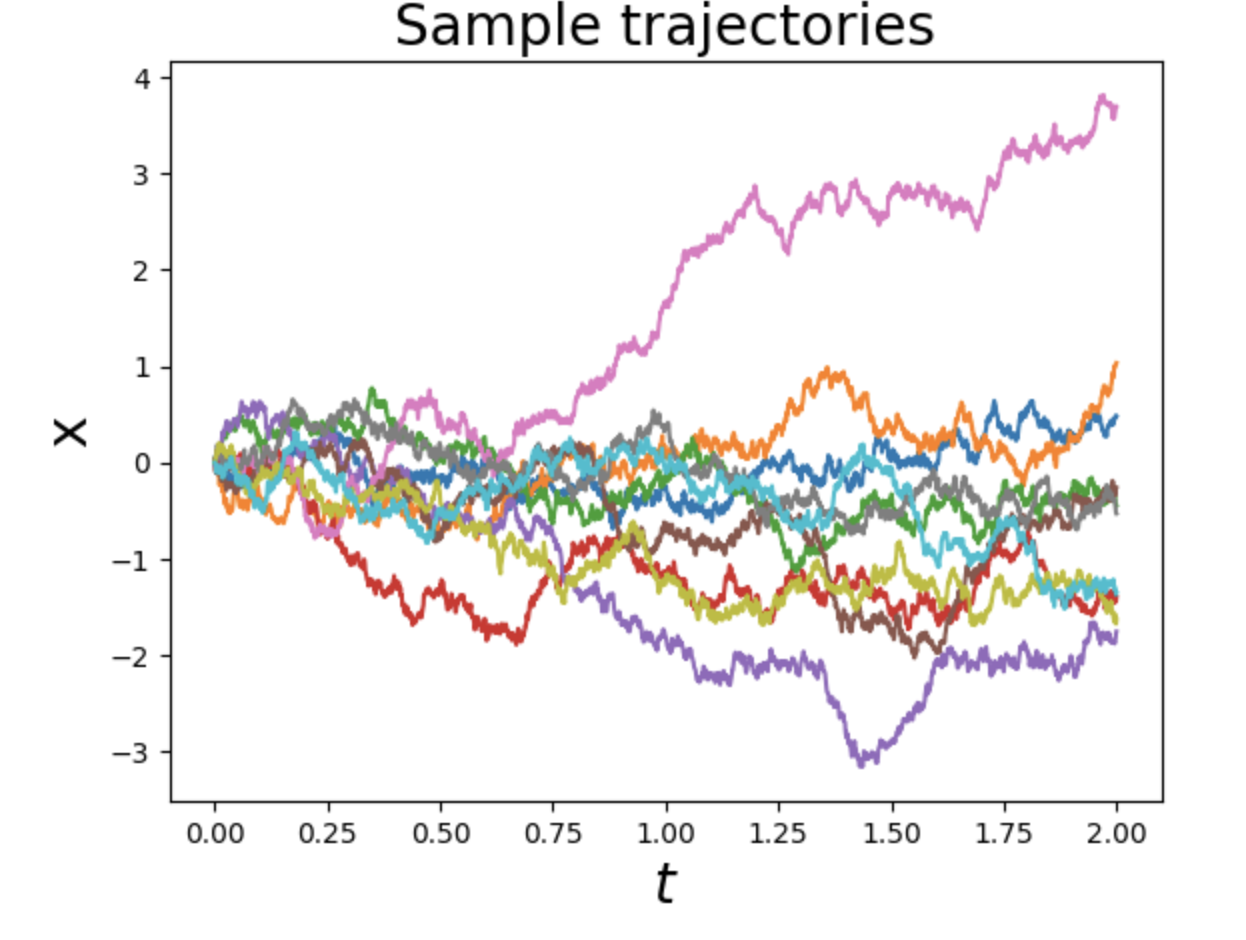

import numpy as np
import matplotlib.pyplot as pltfrom scipy.stats import norm# Simulate SDE with drift function f and noise amplitude g for arbitrary number of steps
def forward_SDE_simulation(x0, nsteps, dt, f, g, params):# Initialize time and a stochastic trajectoryt = 0x_traj = np.zeros((nsteps + 1, *x0.shape))x_traj[0] = np.copy(x0)# Perform many Euler-Maruyama time stepsfor i in range(nsteps):random_normal = np.random.randn(*x0.shape)        # standard normal random numberx_traj[i+1] = x_traj[i] + f(x_traj[i], t, params)*dt + g(x_traj[i], t, params)*np.sqrt(dt)*random_normalt = t + dtreturn x_traj# Drift function for diffusion (returns zeros)
def f_diff_simple(x, t, params):return np.zeros((*x.shape,))# Noise amplitude for diffusion (constant)
def g_diff_simple(x, t, params):sigma = params['sigma']return sigma*np.ones((*x.shape,))# Exact transition probability for 1D diffusion
def transition_probability_diffusion_exact(x, t, params):x0, sigma= params['x0'], params['sigma']pdf = norm.pdf(x, loc=x0, scale=np.sqrt((sigma**2)*t))  # pdf of normal distribution with mean x0 and variance (sigma^2)*treturn pdf#测试例子
sigma = 1         # noise amplitude for 1D diffusionnum_samples = 1000
x0 = np.zeros(num_samples)    # initial condition for diffusionnsteps = 2000      # number of simulation steps
dt = 0.001          # size of small time steps 
T = nsteps*dt
t = np.linspace(0, T, nsteps + 1)params = {'sigma': sigma, 'x0':x0, 'T':T}#生成扩散数据
x_traj = forward_SDE_simulation(x0, nsteps, dt, f_diff_simple, g_diff_simple, params)#可视化扩散过程
# Plot initial distribution (distribution before diffusion)
plt.hist(x_traj[0], density=True, bins=100)
plt.title("$t = 0$", fontsize=20)
plt.xlabel("$x$", fontsize=20)
plt.ylabel("probability", fontsize=20)
plt.show()# Compute exact transition probability 
x_f_min, x_f_max = np.amin(x_traj[-1]), np.amax(x_traj[-1])
num_xf = 1000
x_f_arg = np.linspace(x_f_min, x_f_max, num_xf)
pdf_final = transition_probability_diffusion_exact(x_f_arg, T, params)# Plot final distribution (distribution after diffusion)
plt.hist(x_traj[-1], bins=100, density=True)
plt.plot(x_f_arg, pdf_final, color='black', linewidth=5)
plt.title("$t = $"+str(T), fontsize=20)
plt.xlabel("$x$", fontsize=20)
plt.ylabel("probability", fontsize=20)
plt.show()# Plot some trajectories
sample_trajectories = [0, 1, 2, 3, 4,5,6,7,8,9]
for s in sample_trajectories:plt.plot(t, x_traj[:,s])
plt.title("Sample trajectories", fontsize=20)
plt.xlabel("$t$", fontsize=20)
plt.ylabel("x", fontsize=20)
plt.show()

这段代码模拟了一个简单的随机微分方程（SDE）的演化，特别是一个具有常数扩散系数的一维布朗运动。它使用了欧拉-马里亚马方法（Euler-Maruyama method）来模拟随机微分方程（SDE），并通过几个自定义函数来定义漂移和扩散行为展示了如何模拟和可视化一个简单的随机过程（布朗运动），包括演化的模拟、理论分布的计算和结果的可视化。这对于理解和研究随机过程中的动态行为非常有用。代码主要分为以下几个部分：

1. 导入必要的库

numpy 用于数值计算。
matplotlib.pyplot 用于绘图。
scipy.stats.norm 用于计算正态分布的概率密度函数。

2. SDE模拟函数定义

forward_SDE_simulation：这个函数通过欧拉-马里亚马方法模拟SDE的轨迹。它接收初始条件 x0，时间步数 nsteps，时间步长 dt，漂移函数 f，噪声幅度函数 g，以及其他参数 params。函数返回模拟的轨迹。

3. 漂移和噪声函数

f_diff_simple：返回零数组，表示没有漂移的情况。
g_diff_simple：返回一个常数噪声幅度，这里是 sigma。

4. 精确的转移概率函数

transition_probability_diffusion_exact：计算和返回在给定时间 t，从初始位置 x0 出发，到达位置 x 的概率密度。这是基于正态分布的解析解。

5. 初始化参数和模拟

sigma，num_samples，x0，nsteps，dt，T，params 等参数被初始化。
使用 forward_SDE_simulation 生成一维布朗运动的数据。

6. 可视化

首先绘制初始时刻的分布，应为一个在 x=0 的δ函数。
然后计算并绘制最终时间 T 的理论和模拟分布。理论分布由 transition_probability_diffusion_exact 计算，模拟分布通过直方图展示。
最后，绘制一些样本轨迹，展示随机过程随时间的变化。

更通用的随机微分方程

我们可以考虑前一小节描述的一维随机微分方程的多变量推广。通常，我们可能有
$\dot{\mathbf{x}} = \mathbf{f}(\mathbf{x}, t) + \mathbf{g}(\mathbf{x}, t) \ \boldsymbol{\eta}(t)$
其中 $\mathbf{x}(t) \in \mathbb{R}^N$ ， $\mathbf{f}$ 是一个将 $\mathbf{x}$ 和 t 映射到 $\mathbb{R}^N$ 中向量的函数， $\mathbf{g}$ 是一个依赖于 $\mathbf{x}$ 和 t 的 $\times M$ 矩阵，而 $\boldsymbol{\eta}(t)$ 是一个由独立高斯白噪声项组成的 M维向量。
对应的（按伊藤解释的）Euler-Maruyama 时间步为
$\mathbf{x}(t + \Delta t) = \mathbf{x}(t) + \mathbf{f}(\mathbf{x}(t), t) \Delta t + \mathbf{g}(\mathbf{x}(t), t) \sqrt{\Delta t} \ \mathbf{r}$
其中 $\mathbf{r} = (r_1, ..., r_M)^T$ ，每个 $r_i$ 是从标准正态分布中抽取的样本。
相应的FPE（福克-普朗克方程）为
$\frac{\partial p(\mathbf{x}, t)}{\partial t} = \sum_{j = 1}^N - \frac{\partial}{\partial x_j} \left[ \ f_j(\mathbf{x}, t) p(\mathbf{x}, t) \ \right] + \sum_{j = 1}^N \sum_{k = 1}^N \frac{\partial^2}{\partial x_j \partial x_k} \left[ \ \mathbf{D}_{jk}(\mathbf{x}, t) p(\mathbf{x}, t) \ \right]$
其中 $\mathbf{D}(\mathbf{x}, t) := \frac{1}{2} \mathbf{g}(\mathbf{x}, t) \mathbf{g}(\mathbf{x}, t)^T$ 是一个称为扩散张量的 $\times N$ 矩阵。其元素为
$D_{jk}(\mathbf{x}, t) = \frac{1}{2} \sum_{\ell = 1}^M \sigma_{j \ell}(\mathbf{x}, t) \sigma_{k \ell}(\mathbf{x}, t) \ .$
我们将关注一类稍微不那么通用的多变量SDEs：
$\dot{\mathbf{x}} = \mathbf{f}(\mathbf{x}, t) + g(\mathbf{x}, t) \ \boldsymbol{\eta}(t)$
即 g是 $\mathbf{x}$ 和t的标量函数而不是 $\times M矩$ 阵，并且 M = N。这样解释是每个 $\mathbf{x}$ 的维度都有自己的噪声项（即噪声项不相互耦合），每个噪声项的幅度都是 $g(\mathbf{x}, t)$ 。我们部分是为了简化，部分是因为研究扩散生成模型的研究者倾向于限制在这种情况下。
对于这样的SDEs，福克-普朗克方程简化为
$\frac{\partial p(\mathbf{x}, t)}{\partial t} = - \nabla \cdot \left[ \ \mathbf{f}(\mathbf{x}, t) p(\mathbf{x}, t) \ \right] + \nabla^2 \left[ \ \frac{g(\mathbf{x}, t)^2}{2} p(\mathbf{x}, t) \ \right]\\ = - \nabla \cdot \left[ \ \mathbf{f}(\mathbf{x}, t) p(\mathbf{x}, t) - \nabla \left( \ \frac{g(\mathbf{x}, t)^2}{2} p(\mathbf{x}, t) \ \right) \ \right] \ .$

我们应该使用哪些随机微分方程来对样本进行干扰？

到目前为止，我们只回顾了一些由随机微分方程（SDEs）控制的随机过程的基本事实。我们仍需回答这个问题：给定一个我们感兴趣的分布的样本，我们应该使用什么样的随机过程来对其进行干扰？
以下是一些一般性的考虑：
1 我们希望它足够简单，以至于我们可以准确地求解出当 t 足够大时的 p(x,t)。由于逆向扩散将我们从 p(x,t) 带到我们的目标分布，这意味着我们知道应该从哪个分布中抽样，以生成我们目标分布的逆向扩散样本。
2 我们希望当 t 足够大时，p(x,t) 是一个容易抽样的分布（例如高斯分布）。
3 我们希望样本被强烈地破坏，以至于原始样本几乎没有留下任何痕迹。
第一点排除了大多数可能的随机过程，因为大多数福克-普朗克方程并不能被精确求解。它没有排除的过程类别基本上就是扩散过程和奥恩斯坦-乌伦贝克（OU）类似的过程。
在长时间限制下，扩散过程和OU类似的过程都会将样本转换为来自高斯分布的样本，因此第二点自动得到满足。
为了解决第三点，我们必须确保我们的样本中注入大量噪声。这意味着要么有一个很大的扩散系数，要么扩散很长时间。假设时间固定，我们必须选择某种噪声参数（例如σ）要大。
但“大”对于不同的数据集意味着不同的事情。在发现我们没有足够破坏我们的样本后，手动调整噪声参数会很麻烦。一个解决方案是使用随时间指数增长的噪声：这样，最终，我们应该会有超过足够的噪声。

A. 方差爆炸型随机微分方程（VE SDE）

方差爆炸（VE）随机微分方程（SDE）的定义是
$\dot{\mathbf{x}} = \sqrt{ \frac{d[ \sigma^2(t) ]}{dt} } \ \boldsymbol{\eta}(t)$
其中 σ²(t) 是时间的严格增函数，且 x(t)∈Rⁿ。相应的转移概率是
$KaTeX parse error: {split} can be used only in display mode.$
直觉是我们将样本置于一个噪声规模不断增加的扩散过程中 σ²(t)。
我们应该为 σ²(t) 选择什么函数？本着上述第三点的精神，我们可以选择一个指数增长的函数：
$\sigma^2(t) := \sigma^2_{min} \left( \frac{\sigma^2_{max}}{\sigma^2_{min}} \right)^{t/T} = \sigma^2_{min} \exp\left\{ \frac{t}{T} \log\left( \frac{\sigma^2_{max}}{\sigma^2_{min}} \right) \right\}$
其中 T 是我们对样本进行扩散的时间长度。当然，重要的不是确切的参数化，而是 σ²(t) 是指数增长的。
在宋等人 2021 年的研究中，他们建议 σ_min² = (0.01)²。他们推荐，与宋和厄蒙 2020 年的研究一致，选择 σ_max² 为所有训练样本对之间欧几里得距离平方的最大值。

B. 方差保持型随机微分方程（VP SDE）

方差保持（VP）随机微分方程（SDE）的定义是
$\dot{\mathbf{x}} = - \frac{\beta(t)}{2} \mathbf{x} + \sqrt{ \beta(t) } \ \boldsymbol{\eta}(t)$
其中 β(t) 是时间的严格增函数，且 x(t)∈Rⁿ。相应的转移概率是
$KaTeX parse error: {split} can be used only in display mode.$
其中
$KaTeX parse error: {split} can be used only in display mode.$
直觉是我们将样本的每个维度独立地置于一个OU过程中，通过一个严格增函数 β(t) 调节其向稳态（即均值为0且方差为1的高斯分布）的收敛。随着 β(t) 的增加，样本被越来越紧迫地推向零。
为了明确说明，这个过程的长时间/稳态分布与其初始条件无关，是
$\mathbf{x}, t) \xrightarrow{t \to \infty} p_{ss}(\mathbf{x}) = \frac{1}{\left[ \sqrt{2 \pi} \right]^N} \exp\left\{ - \frac{\mathbf{x}^2}{2} \right\} = \prod_{j = 1}^N \frac{1}{\sqrt{2 \pi} } \exp\left\{ - \frac{x_j^2}{2} \right\}$
即它是 N 个标准正态分布的乘积。
我们应该为 β(t) 选择什么函数？本着上述第三点的精神，我们可以选择一个线性增长的函数：
$\beta(t) := \beta_{min} + (\beta_{max} - \beta_{min}) \frac{t}{T}$
其中 T 是我们对样本运行该过程的时间长度。选择 β(t) 线性增长而不是指数增长也是可以的，因为从上述 μ(t) 和 σ²(t) 的表达式中可以看出，样本以由 β(t) 决定的速率指数级快速收敛到稳态。
在宋等人 2021 年的研究中，他们建议 β_min = 0.1 和 β_max = 20，这与何等人 2020 年的选择一致。

C. 次方差保持型随机微分方程（sub-VP SDE）

次方差保持（sub-VP）随机微分方程（SDE）的定义是
$\dot{\mathbf{x}} = - \frac{\beta(t)}{2} \mathbf{x} + \sqrt{ \beta(t) \left[ 1 - e^{- 2 \int_0^t \beta(s) ds} \right] } \ \boldsymbol{\eta}(t)$
其中 β(t) 是时间的严格增函数，且 x(t)∈Rⁿ。相应的转移概率是
$KaTeX parse error: {split} can be used only in display mode.$
其中
$KaTeX parse error: {split} can be used only in display mode.$
换句话说，这个SDE的行为就像VP SDE一样，除了它的方差总是更小（因此得名）。
长时间/稳态行为也是相同的（在 t→∞ 极限下，我们得到 N 个标准正态分布的乘积）。
宋等人 2021 年使用的 β(t) 函数与他们用于VP SDE的函数相同。

1.1：欧拉-丸山示例

用于模拟以下随机微分方程的欧拉-丸山时间步长：
(1) $\dot{x} = \sigma \sqrt{x} \ \eta(t)$
(2) $\dot{x} = \frac{1}{\tau} \left[ \mu - x \right] + \sigma \sqrt{\frac{2}{\tau}} \ \eta(t) \ .$
(3) $KaTeX parse error: {split} can be used only in display mode.$
(4) $KaTeX parse error: {split} can be used only in display mode.$

1.2：扩散保持分布的均值

我们是否希望保持目标分布的均值？如果是的话，扩散可能比OU过程更好，因为扩散保持了分布的均值。
考虑一维扩散，其相应的转移概率是
$x_0, 0) = \frac{1}{\sqrt{2 \pi \sigma^2 t}} \exp\left\{ - \frac{(x - x_0)^2}{2 \sigma^2 t} \right\} \ .$
给定任意初始条件 $p(x, 0) = p_0(x)$ ，扩散方程的一般解为
$\int_{-\infty}^{\infty} p(x, t | x_0, 0) p_0(x_0) \ dx_0 \ .$
证明
$\langle x(t) \rangle := \int x \ p(x, t) \ dx = \int x_0 p_0(x_0) \ dx_0 \ .$

1.3：OU过程的长时间行为

考虑一维OU过程
$\dot{x} = \frac{1}{\tau} \left[ \mu - x \right] + \sigma \sqrt{\frac{2}{\tau}} \ \eta(t) \ ,$
我们发现其转移概率是
$x_0, 0) = \frac{1}{\sqrt{2 \pi s(t)^2}} \exp\left\{ - \frac{[ x - \mu(t) ]^2}{2 s(t)^2} \right\}$
其中
$KaTeX parse error: {split} can be used only in display mode.$
证明，对于任意初始分布 $p(x, 0) = p_0(x)$ ，我们有
$\int_{-\infty}^{\infty} p(x, t | x_0, 0) p_0(x_0) \ dx_0 \ \xrightarrow{t \to \infty} p_{ss}(x) \\= \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left\{ - \frac{(x - \mu)^2}{2 \sigma^2} \right\} \ .$
特别需要注意的是，OU过程不保持分布的均值！

1.4：扩散对高斯混合的影响

考虑一个具有M个混合成分的一维高斯混合模型
$p_0(x) = \sum_{j = 1}^M w_j \ \frac{1}{\sqrt{2 \pi s_j^2}} \exp\left\{ - \frac{[ x - \mu_j ]^2}{2 s_j^2} \right\}$
其中 $\mu_j$ 是第 j个混合成分的均值, $s_j$ 是第 j个混合成分的标准差。
假设我们使用这个高斯混合作为一维扩散的初始条件。提醒一下，一维扩散的转移概率为
$x_0, 0) = \frac{1}{\sqrt{2 \pi \sigma^2 t}} \exp\left\{ - \frac{(x - x_0)^2}{2 \sigma^2 t} \right\} \ .$
证明
$KaTeX parse error: {split} can be used only in display mode.$
换句话说，扩散一个高斯混合会得到另一个高斯混合，其各个成分的方差都会增加。

1.5：福克-普朗克方程的推导

让我们尝试推导一维伊藤解释下的随机微分方程的福克-普朗克方程
$\dot{x} = f(x, t) + g(x, t) \ \eta(t)$
我们提醒读者这是
$\frac{\partial p(x, t)}{\partial t} = - \frac{\partial}{\partial x} \left[ \ f(x, t) p(x, t) \ \right] + \frac{\partial^2}{\partial x^2} \left[ \ \frac{g(x, t)^2}{2} p(x, t) \ \right] \ .$

从欧拉-马鲁亚马时间步的表达式开始。证明如果

$x_{n+1} = x_n + f(x_n, t) \Delta t + g(x_n, t) \sqrt{t} \ r \ ,$
从欧拉-马鲁亚马时间步的表达式开始。证明如果
$p(x_{n+1}, t + \Delta t | x_n, t) = \frac{1}{\sqrt{2 \pi g(x_n,t)^2 \Delta t}} \exp\left\{ - \frac{(x_{n+1} - x_n - f(x_n, t) \Delta t)^2}{2 g(x_n, t)^2 \Delta t} \right\} \ .$
提示：正态随机变量的线性组合也是正态随机变量。

证明（把上面条件概率表示成对delta T导数形式，然后在对delta T积分把T去除）

$p(x_{n+1}, t + \Delta t | x_n, t) = \int_{-\infty}^{\infty} \frac{dp_n}{2 \pi} \ \exp\left\{ - i p_n \left[ x_{n+1} - x_n - f(x_n, t) \Delta t \right] - \frac{g(x_n, t)^2}{2} p_n^2 \Delta t \right\} \ .$
提示：如果这太让人困惑，不妨先尝试计算高斯积分
$\int_{-\infty}^{\infty} \frac{dp}{2 \pi} \ \exp\left\{ - i p \left[ x - \mu \right] - \frac{\sigma^2}{2} p^2 \right\} \ .$

请注意

$\int_{-\infty}^{\infty} dy \ p(x, t | y, t') p(y, t')$
其中 t’ 是 t 之前的任何时间，即 t’ ≤ t。特别是，我们有这样的情况：
$\Delta t) = \int_{-\infty}^{\infty} dy \ p(x, t + \Delta t | y, t) p(y, t)$
或者Δt非常小。证明，在Δt的一阶情况下，
$\Delta t) = \int_{-\infty}^{\infty} dy \int_{-\infty}^{\infty} \frac{dp}{2 \pi} \ e^{- i p (x - y)} \left\{ 1 + \left[ i p f(y, t) + (ip)^2 \frac{g(y, t)^2}{2} \right] \Delta t \ \right\} p(y, t)$

回忆一下狄拉克δ函数具有积分表示法

$\delta(x - y) = \int_{-\infty}^{\infty} \frac{dp}{2\pi} \ e^{- i p (x - y)} \ .$
通过分部积分法论证你的表达式 p(x,t+Δt) 暗示了
$\Delta t) = p(x, t) + \left\{ \ - \frac{\partial}{\partial x}\left[ f(x, t) p(x, t) \right] + \frac{\partial^2}{\partial x^2}\left[ \frac{g(x, t)^2}{2} p(x, t) \right] \ \right\} \Delta t \ .$
利用这一点得出结论，p(x,t) 满足福克-普朗克方程。

反向扩散

我们如何“撤销”我们在前向扩散过程中添加到样本中的噪声？尽管这有点违反直觉——例如，我们期望通过扩散看到奶油和咖啡混合，但不期望它们会自发分离——事实证明，定义一个由随机微分方程（SDE）控制的随机过程的时间逆过程在数学上是直截了当的。时间逆过程本身是一个由SDE控制的随机过程，其概率密度随时间演变遵循福克-普朗克方程。

反转一维扩散

回想一下，一维扩散（在时间T内）可以通过随机微分方程（SDE）来描述。
$\dot{x} = \sigma \ \eta(t) \ .$
直观上来说，扩散会使事物扩散开来。我们会期望这一过程的时间逆向会使事物重新聚集。
有一种随机过程会使事物聚集，而不是扩散开来，那就是OU过程。某种OU过程可能是一维扩散的时间逆过程吗？事实证明，所描述的OU过程
$\dot{x} = \frac{x_0 - x}{T - t} + \sigma \ \eta(t)$
是一个从点 $x_0$ 开始、并在时间 T内扩散开的扩散过程的时间逆过程。换句话说，这个过程会压缩一个高斯分布，直到它在时间 T $时变成一个以$ x_0 $为中心的狄拉克函数。 转移概率也是相反的： $ q(x, t | x_0, 0) = \frac{1}{\sqrt{2 \pi \sigma^2 (T - t)}} \exp\left{ - \frac{(x - x_0)^2}{2 \sigma^2 (T - t)} \right} \ . $ 为了不将这些概率与前向过程的概率混淆，我们将用 q 而不是 p 来表示它们。 由于逆过程也受到随机微分方程（ S D E ）的约束，我们可以使用欧拉 - 马里亚马时间步来模拟它；在这里，我们将有 $ x(t + \Delta t) = x(t) + \frac{x_0 - x}{T - t} \Delta t + \sigma \sqrt{\Delta t} \ r \ . $ 注意，我们使用的约定是时间向 * 前 * 运行，从 t = 0 到 t = T 。人们也使用时间向 * 后 * 运行的约定（从 t = T 到 t = 0 ），在这种情况下，我们将有 $ x(t - \Delta t) = x(t) - \frac{(x_0 - x)}{t} \Delta t + \sigma \sqrt{\Delta t} \ r \ .$
它们在数学上是等价的，所以在进行模拟时你可以使用任何一个。

反转更一般的随机过程

有没有一些系统的方法来推导逆过程？幸运的是，有这样的方法；对于一维伊藤解释的随机微分方程（具有状态独立的噪声）
$\dot{x} = f(x, t) + g(t) \ \eta(t) \ ,$
时间逆过程（继续使用时间向前运行的约定，从 t = 0 到 t = T）是
$\dot{x} = - f(x, T - t) + g(T - t)^2 \frac{\partial}{\partial x} \log p(x, T - t) + g(T - t) \ \eta(t) \ .$
如果 p(x, t)描述了从某个特定初始条件开始的前向过程的时间演化，那么 q(x, t)，即逆过程的时间演化，满足
$q (x, t) = p (x, T - t)$
即它是相同的时间演化，但是向’后’运行。
对于具有各向同性状态独立噪声的 N $维伊藤解释的随机微分方程 $ \dot{\mathbf{x}} = \mathbf{f}(\mathbf{x}, t) + g(t) \ \boldsymbol{\eta}(t) \ , $ 时间逆过程是 $ \dot{\mathbf{x}} = - \mathbf{f}(\mathbf{x}, T - t) + g(T - t)^2 \ \nabla_{\mathbf{x}} \log p(\mathbf{x}, T - t) + g(T - t) \ \boldsymbol{\eta}(t) \ . $ 我们有更一般的关系 $ q(\mathbf{x}, t) = p(\mathbf{x}, T - t) \ .$

引出得分函数

上述逆过程的表达式中包含了一个看起来很有趣的函数：所谓的得分函数，定义为
$\mathbf{s}(\mathbf{x}, t) := \nabla_{\mathbf{x}} \ p(\mathbf{x}, t) \ .$
如果我们想要在某些噪声上运行逆过程，并将其转换为我们目标分布的样本，我们需要知道得分函数。这实际上是这整个生成模型方法的关键难点。
为什么这会困难？我们不知道 $p(\mathbf{x}, t)!$ 如果我们知道，我们可以直接从中抽样，而不是进行逆向扩散。
虽然这看起来像是先有鸡还是先有蛋的问题，情况并没有看上去那么糟糕。我们确实*需要学习得分函数，但这比直接学习 $p(\mathbf{x}, t)$ 更容易，后者还需要我们学习一个归一化因子（这很难）。

得分函数的例子

得分函数将每个时间步的随机过程与一个向量场关联起来。每个小向量都指向概率增加的方向。让我们看几个例子来建立直觉。

从点质量出发的一维扩散

考虑一维扩散的情况，初始条件为位于 $x_0$ 的delta函数。时间依赖的概率是
$\frac{1}{\sqrt{2 \pi \sigma^2 t}} \exp\left\{ - \frac{(x - x_0)^2}{2 \sigma^2 t} \right\} \ .$
然后得分函数是
$\frac{\partial}{\partial x} \log p(x, t) = - \frac{(x - x_0)}{\sigma^2 t} \ .$

从点质量出发的一维OU过程

考虑上述定义的一维OU过程，初始条件为位于 $x_0$ 的delta函数。时间依赖的概率是
$\frac{1}{\sqrt{2 \pi s(t)^2}} \exp\left\{ - \frac{[ x - \mu(t) ]^2}{2 s(t)^2} \right\} \ .$
然后得分函数是
$\frac{\partial}{\partial x} \log p(x, t) = - \frac{[ x - \mu(t) ]}{s(t)^2} \ .$

从高斯混合出发的一维扩散

如考虑一个有M个混合成分的一维高斯混合模型
$p_0(x) = \sum_{j = 1}^M w_j \ \frac{1}{\sqrt{2 \pi s_j^2}} \exp\left\{ - \frac{[ x - \mu_j ]^2}{2 s_j^2} \right\}$
其中 $\mu_j$ 是混合成分j的均值， $s_j$ 是混合成分j的标准差。扩散这个混合模型产生
$KaTeX parse error: {split} can be used only in display mode.$
因此，相应的得分函数是
$\frac{\partial}{\partial x} \log p(x, t) = - \frac{1}{p(x, t)} \sum_{j = 1}^M w_j \frac{(x - \mu_j)}{s_j^2 + \sigma^2 t} \ \frac{1}{\sqrt{2 \pi (s_j^2 + \sigma^2 t)}} \exp\left\{ - \frac{[ x - \mu_j ]^2}{2 (s_j^2 + \sigma^2 t)} \right\} \ .$

基本示例代码

让我们尝试实现对应于一维扩散的反向过程（解析解）。我们将重用上面的一些代码（用于模拟正向过程）；我们只需要为反向过程定义漂移和噪声函数。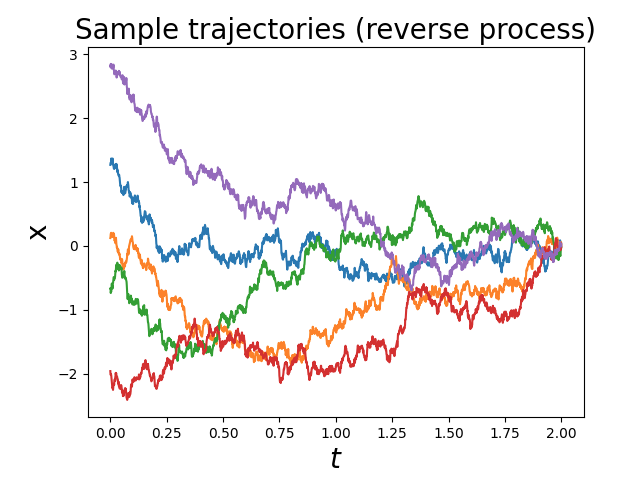

# Drift function for a reverse process. More general than 1D diffusion.
def f_diff_simple_rev(x, t, params):T = params['T']return - f_diff_simple(x, T-t, params) + (g_diff_simple(x, T-t, params)**2)*score(x, T-t, params)# Noise function for 1D diffusion (constant)
def g_diff_simple_rev(x, t, params):sigma = params['sigma']return sigma*np.ones(len(x))# The score function for 1D diffusion from a point source. Score = grad log p(x,t)
def score(x, t, params):x0 = params['x0']sigma = params['sigma']score_ = (x0 - x)/((sigma**2)*(t))return score_#测试例子
sigma = 1         # noise amplitude for 1D diffusionnum_samples = 1000
x0 = np.zeros(num_samples)    # initial condition for diffusionnsteps = 2000      # number of simulation steps
dt = 0.001          # size of small time steps 
T = nsteps*dt
t = np.linspace(0, T, nsteps + 1)params = {'sigma': sigma, 'x0':x0, 'T':T}#生成前向过程数据，用解析解表示方式取得逆高斯过程的解
x_traj = forward_SDE_simulation(x0, nsteps, dt, f_diff_simple, g_diff_simple, params)
x_traj_rev = forward_SDE_simulation(x_traj[-1], nsteps, dt, f_diff_simple_rev, g_diff_simple_rev, params)#可视化逆高斯过程
# Compute exact transition probability 
x_f_min, x_f_max = np.amin(x_traj[-1]), np.amax(x_traj[-1])
num_xf = 1000
x_f_arg = np.linspace(x_f_min, x_f_max, num_xf)
pdf_final = transition_probability_diffusion_exact(x_f_arg, T, params)# Plot final distribution (distribution after diffusion / before reverse diffusion)
plt.hist(x_traj[-1], bins=100, density=True)
plt.plot(x_f_arg, pdf_final, color='black', linewidth=5)
plt.title("$t = $"+str(T), fontsize=20)
plt.xlabel("$x$", fontsize=20)
plt.ylabel("probability", fontsize=20)
plt.show()# Plot initial distribution (distribution before diffusion / after reverse diffusion)
#fig, ax = plt.subplots(1, 2, width=)
plt.hist(x_traj_rev[-1], density=True, bins=100, label='rev. diff.')
plt.hist(x_traj[0], density=True, bins=100, label='true')plt.title("$t = 0$", fontsize=20)
plt.xlabel("$x$", fontsize=20)
plt.ylabel("probability", fontsize=20)
plt.legend(fontsize=15)
plt.show()# Plot some trajectories
sample_trajectories = [0, 1, 2, 3, 4]
for s in sample_trajectories:plt.plot(t, x_traj_rev[:,s])
plt.title("Sample trajectories (reverse process)", fontsize=20)
plt.xlabel("$t$", fontsize=20)
plt.ylabel("x", fontsize=20)
plt.show()

这段代码定义了涉及一维扩散过程的逆向过程的几个函数：

f_diff_simple_rev(x, t, params) - 这是逆向过程的漂移函数。它使用参数T（总时间）来计算时间T-t时的正向过程的漂移和噪声函数，然后计算得分函数（概率密度函数的梯度的对数）。函数返回逆向过程的漂移，这是正向漂移的负值加上噪声函数的平方乘以得分函数。
g_diff_simple_rev(x, t, params) - 这是逆向过程的噪声函数。它返回一个与输入x长度相同、值为sigma的常数数组。这里的sigma是扩散过程的标准差，由参数字典params提供。
score(x, t, params) - 这是从点源开始的一维扩散过程的得分函数。得分函数是概率密度函数对数的梯度。在这个函数中，它根据位置x、时间t、初始位置x0和扩散系数sigma来计算得分。

这些函数通常用于模拟和分析随机过程中的路径依赖性，特别是在金融数学和物理学中的扩散过程。逆过程的概念在期权定价和风险管理中尤为重要，因为它可以帮助理解和预测在给定终点条件下系统的行为。

几个相关推导

为什么逆向随机过程有效？

考虑一个一维的由伊藤解释的随机微分方程（SDE）
$\dot{x} = f(x, t) + g(t) \ \eta(t) \ ,$
其时间逆过程应为
$\dot{x} = - f(x, T - t) + g(T - t)^2 \frac{\partial}{\partial x} \log p(x, T - t) + g(T - t) \ \eta(t) \ .$
如果后者确实是前者的时间逆过程，我们期望
$\ .$
注意，前向过程满足福克-普朗克方程
$\frac{\partial p(x, t)}{\partial t} = - \frac{\partial}{\partial x} \left[ \ f(x, t) p(x, t) \ \right] + \frac{\partial^2}{\partial x^2} \left[ \ \frac{g(x, t)^2}{2} p(x, t) \ \right] \ .$
通过时间反转，我们发现 $p (x, T - t)$ 满足
$\frac{\partial p(x, T - t)}{\partial t} = \frac{\partial}{\partial x} \left[ \ f(x, T-t) p(x, T-t) \ \right] - \frac{\partial^2}{\partial x^2} \left[ \ \frac{g(x, T-t)^2}{2} p(x, T-t) \ \right] \ .$
利用这一事实来证明 $q (x, t) = p (x, T - t)$ 是福克-普朗克方程的解
$\frac{\partial q(x, t)}{\partial t} = - \frac{\partial}{\partial x} \left[ \ \left( f(x, T-t) - g(T-t)^2 \frac{\partial}{\partial x} \log p(x, T-t) \right) q(x, t) \ \right] + \frac{\partial^2}{\partial x^2} \left[ \ \frac{g(x, T-t)^2}{2} q(x, t) \ \right] \ ,$
从而证明我们确实写下了描述逆过程的SDE。

为什么逆向随机过程有效？

考虑一个 $N$ 维的由伊藤解释的随机微分方程（SDE）
$\dot{\mathbf{x}} = \mathbf{f}(\mathbf{x}, t) + g(t) \ \boldsymbol{\eta}(t) \ ,$
其时间逆过程应为
$\dot{\mathbf{x}} = - \mathbf{f}(\mathbf{x}, T - t) + g(T - t)^2 \ \nabla_{\mathbf{x}} \log p(\mathbf{x}, T - t) + g(T - t) \ \boldsymbol{\eta}(t) \ .$
我们期望
$q(\mathbf{x}, t) = p(\mathbf{x}, T - t) \ .$
通过从之前问题中推广论点，展示 $q(\mathbf{x}, t) = p(\mathbf{x}, T - t)$ 满足正确的福克-普朗克方程，从而证明我们确实写下了描述逆过程的SDE。

通过学习方式求解逆高斯噪声分布

下面代码是一个一维扩散生成模型的实现示例，展示了如何通过模拟随机微分方程的扩散和逆向过程来生成和恢复数据。代码里面几个重要点：训练数据是什么，模型训练的是什么（预测逆向图像分布？），推理时候输入是什么
1. 导入库
代码首先导入了一系列Python库，这些库主要用于数据处理、数学运算、图形可视化和深度学习模型构建。具体包括：

matplotlib 和 seaborn：用于数据可视化。
pandas 和 numpy：提供数据操作和数学运算支持。
torch：PyTorch库，用于构建和训练深度学习模型。
itertools 和 tqdm：用于循环操作和进度条显示。

创建数据分布
使用torch.distributions构建了一个混合高斯分布，这个分布由两个不同均值（-4和4）且相同标准差（1）的正态分布组成。这种混合模型可以模拟具有两个明显峰值的数据分布。
3. 数据可视化
使用seaborn的histplot函数绘制了生成的数据集的直方图。这有助于直观地查看数据的分布情况，确认是否符合预期的双峰分布。
4. 扩散过程
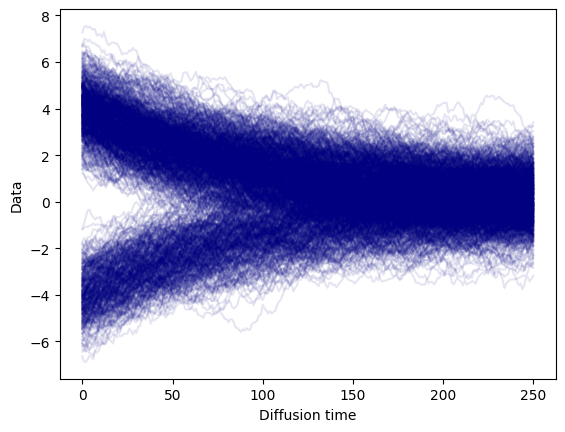
定义了do_diffusion函数，该函数通过多步迭代模拟数据的扩散过程。在每一步中，当前数据点根据正态分布进行随机扰动，逐渐向噪声状态转变。这个过程可以视为数据通过随机微分方程的演化。
5. 可视化扩散过程
通过绘制扩散过程中的数据点，展示了数据随时间的演变过程。这有助于理解数据是如何从初始状态逐渐“扩散”到一个近乎随机的状态。
6. 计算损失
compute_loss函数用于计算在扩散模型中的损失。这个函数考虑了从数据的扩散状态逆向恢复到原始状态的过程，通过比较正向扩散模型和逆向恢复模型的概率分布来计算损失。
7. 模型训练
设置了一个简单的神经网络，用于在逆向过程中预测数据点的均值和方差。使用AdamW优化器进行参数优化，通过最小化损失函数来训练模型。
8. 可视化训练过程
绘制了训练过程中损失函数的变化曲线，使用对数尺度展示损失的下降，帮助观察训练的效果和速度。
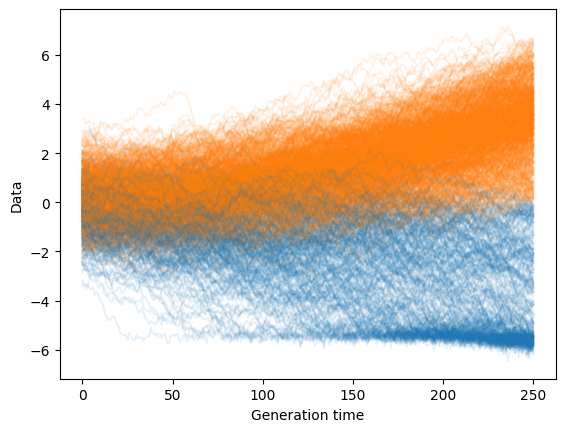
9. 生成新数据
sample_reverse函数实现了从完全随机的噪声状态开始，通过逆向运行扩散过程来生成新的数据样本。这个过程展示了如何从无序状态恢复出有序且具有特定分布的数据。
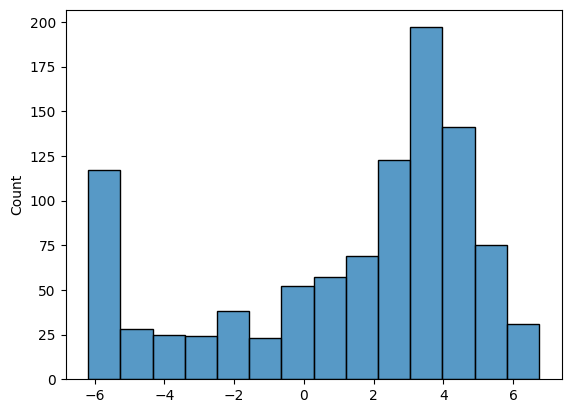
10. 可视化生成的数据
对逆向生成的数据样本进行可视化，并使用直方图展示了最终生成的数据分布情况。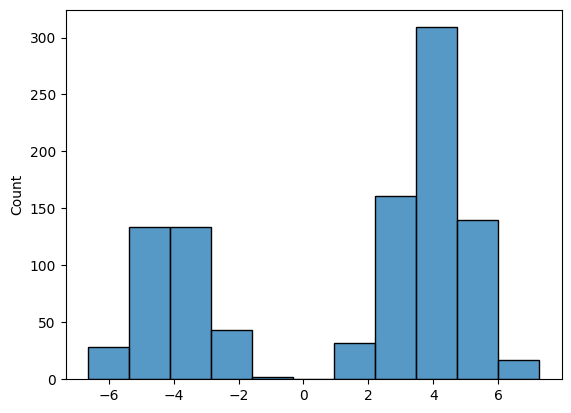

import matplotlib.pyplot as plt
import matplotlib as mpl
import pandas as pd
import numpy as np
import torch
import seaborn as sns
import itertools
from tqdm.auto import tqdmdata_distribution = torch.distributions.mixture_same_family.MixtureSameFamily(torch.distributions.Categorical(torch.tensor([1, 2])),torch.distributions.Normal(torch.tensor([-4., 4.]), torch.tensor([1., 1.]))
)dataset = data_distribution.sample(torch.Size([1000, 1]))
sns.histplot(dataset[:, 0])
plt.show()# we will keep these parameters fixed throughout
TIME_STEPS = 250
BETA = 0.02def do_diffusion(data, steps=TIME_STEPS, beta=BETA):# perform diffusion following equation 2# returns a list of q(x(t)) and x(t)# starting from t=0 (i.e., the dataset)distributions, samples = [None], [data]xt = datafor t in range(steps):q = torch.distributions.Normal(np.sqrt(1 - beta) * xt,np.sqrt(beta))xt = q.sample()distributions.append(q)samples.append(xt)return distributions, samples_, samples = do_diffusion(dataset)for t in torch.stack(samples)[:, :, 0].T[:1000]:plt.plot(t, c='navy', alpha=0.1)
plt.xlabel('Diffusion time')
plt.ylabel('Data')
plt.show()def compute_loss(forward_distributions, forward_samples, mean_model, var_model):# here we compute the loss in equation 3# forward = q , reverse = p# loss for x(T)p = torch.distributions.Normal(torch.zeros(forward_samples[0].shape),torch.ones(forward_samples[0].shape))loss = -p.log_prob(forward_samples[-1]).mean()#print(len(forward_samples))#print(len(forward_samples[-1]))for t in range(1, len(forward_samples)):xt = forward_samples[t]         # x(t)xprev = forward_samples[t - 1]  # x(t-1)q = forward_distributions[t]    # q( x(t) | x(t-1) )# normalize t between 0 and 1 and add it as a new column# to the inputs of the mu and sigma networksxin = torch.cat((xt, (t / len(forward_samples)) * torch.ones(xt.shape[0], 1)),dim=1)# compute p( x(t-1) | x(t) ) as equation 1mu = mean_model(xin)sigma = var_model(xin)p = torch.distributions.Normal(mu, sigma)# add a term to the lossloss -= torch.mean(p.log_prob(xprev))loss += torch.mean(q.log_prob(xt))return loss / len(forward_samples)mean_model = torch.nn.Sequential(torch.nn.Linear(2, 4), torch.nn.ReLU(),torch.nn.Linear(4, 1)
)
var_model = torch.nn.Sequential(torch.nn.Linear(2, 4), torch.nn.ReLU(),torch.nn.Linear(4, 1), torch.nn.Softplus()
)optim = torch.optim.AdamW(itertools.chain(mean_model.parameters(), var_model.parameters()),lr=1e-2, weight_decay=1e-6,
)loss_history = []
bar = tqdm(range(2000))
for e in bar:forward_distributions, forward_samples = do_diffusion(dataset)optim.zero_grad()loss = compute_loss(forward_distributions, forward_samples, mean_model, var_model)loss.backward()optim.step()bar.set_description(f'Loss: {loss.item():.4f}')loss_history.append(loss.item())plt.plot(loss_history)
plt.yscale('log')
plt.ylabel('Loss')
plt.xlabel('Training step')
plt.show()def sample_reverse(mean_model, var_model, count, steps=TIME_STEPS):p = torch.distributions.Normal(torch.zeros(count, 1), torch.ones(count, 1))xt = p.sample()sample_history = [xt]for t in range(steps, 0, -1):xin = torch.cat((xt, t * torch.ones(xt.shape) / steps), dim=1)p = torch.distributions.Normal(mean_model(xin), var_model(xin))xt = p.sample()sample_history.append(xt)return sample_historysamps = torch.stack(sample_reverse(mean_model, var_model, 1000))for t in samps[:,:,0].T[:1000]:plt.plot(t, c='C%d' % int(t[-1] > 0), alpha=0.1)
plt.xlabel('Generation time')
plt.ylabel('Data')
plt.show()sns.histplot(samps[-1, :, 0])
plt.show()