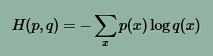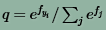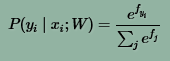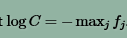本文主要是介绍神经网络 part2 :Softmax classifier,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
转载自皓月如我的CSDN博客,原始链接地址。 http://blog.csdn.net/fm0517/article/details/52051198
*此系列为斯坦福李飞飞团队的系列公开课“cs231n convolutional neural network for visual recognition ”的学习笔记。本文主要是对module 1 的part2 Linear classification: Support Vector Machine, Softmax 的翻译与学习。Softmax classifier是另一种常用的分类器,它可以看作是二类罗杰斯特回归对于多种分类情况的推广。在Softmax classifier中,判别函数与SVM一致,但是损失函数被重新定义为:

可以从信息论的角度来解读Softmax classifier:
p为正确的分类,q为算法估计出的分类。
Softmax classifier就是要缩小p,q之间的信息熵。其中q是对样本分类的估计:
p是样本的正确分类,用一个向量表示,这个向量中只有一个维度是1,其余全部都是0.
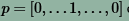
从概率的角度来解读:
上式表示在W的条件下,对输入Xi进行分类,Xi属于第yi类的概率。对于正确的分类,我们要尽力缩小否定的可能性(minimizing the negative log likelihood of the correct class),我们可以用极大似然估计来解决这个问题。也可以用极大后验概率估计(Maximum a posteriori (MAP) )来解决这个问题。
数据稳定性 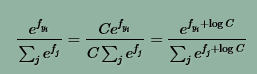
C是一个常熟,它的选取通常遵循准则:
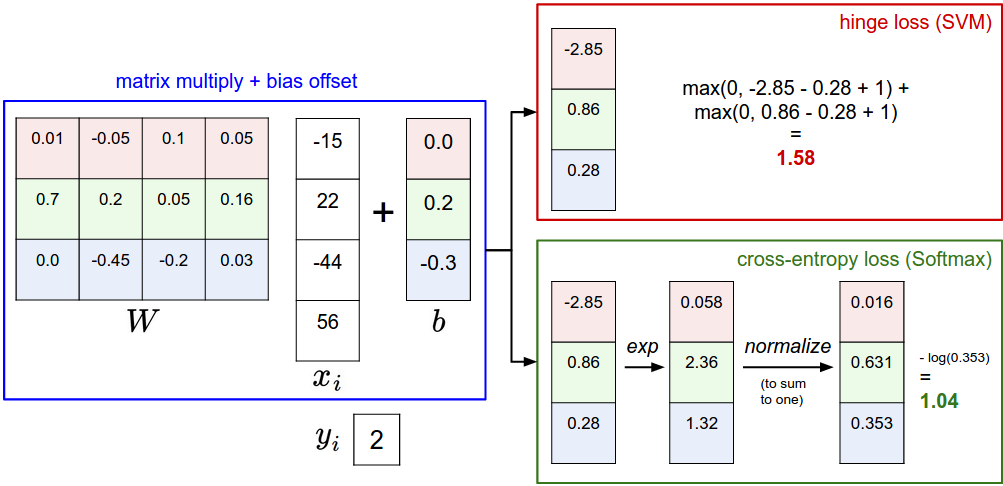
svm vs softmax
SVM与softmax的具体操作过程如上图所示,值得注意的是,最后得到的损失函数并不具备可比性。只有用相同的分类器得到的损失函数才具备可比性。
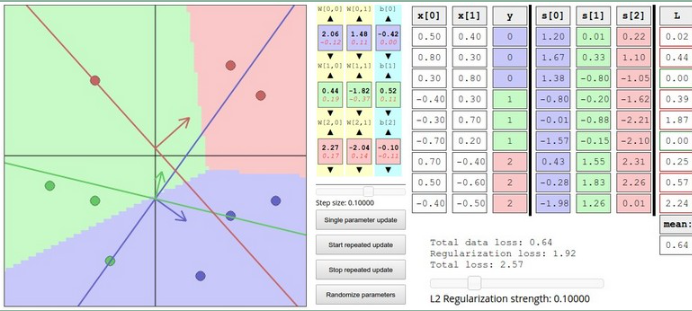
softmax为图片是否属于某个类别提供了一个“概率”。之所以打引号,是因为进过softmax对判别函数的处理后,所有判别的得分之和是1。例如:
如果将W整体拉伸,缩小一倍。判别的结果将变为:可以看出,“概率”的分布更加分散了。
实践中,SVM和softmax常常的性能常常不相上下。差别微乎其微。
这篇关于神经网络 part2 :Softmax classifier的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!