傅里叶变换(书上居然写错了，作者不懂居然还能写这么多。)

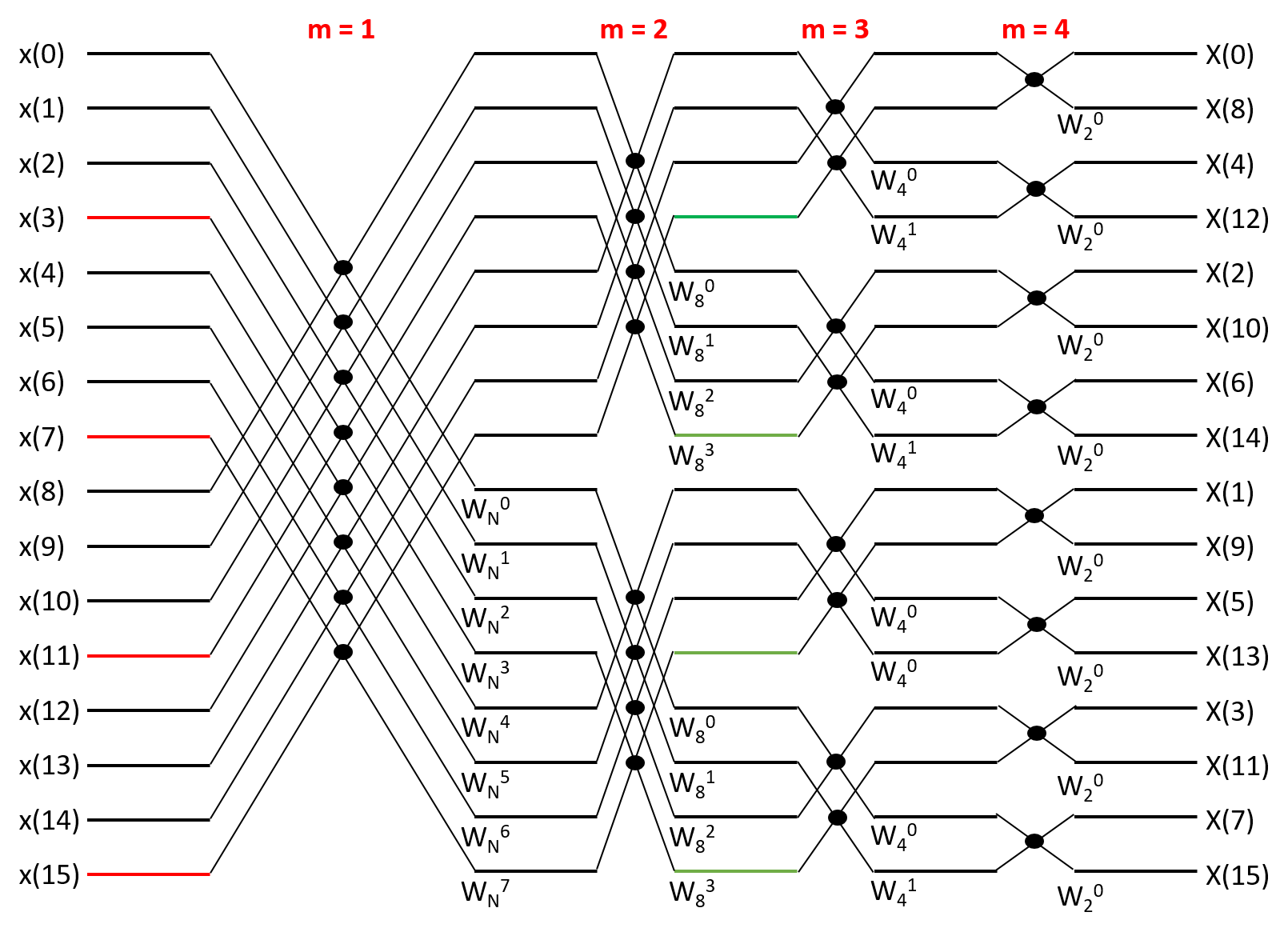
本文主要是介绍傅里叶变换(书上居然写错了，作者不懂居然还能写这么多。)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

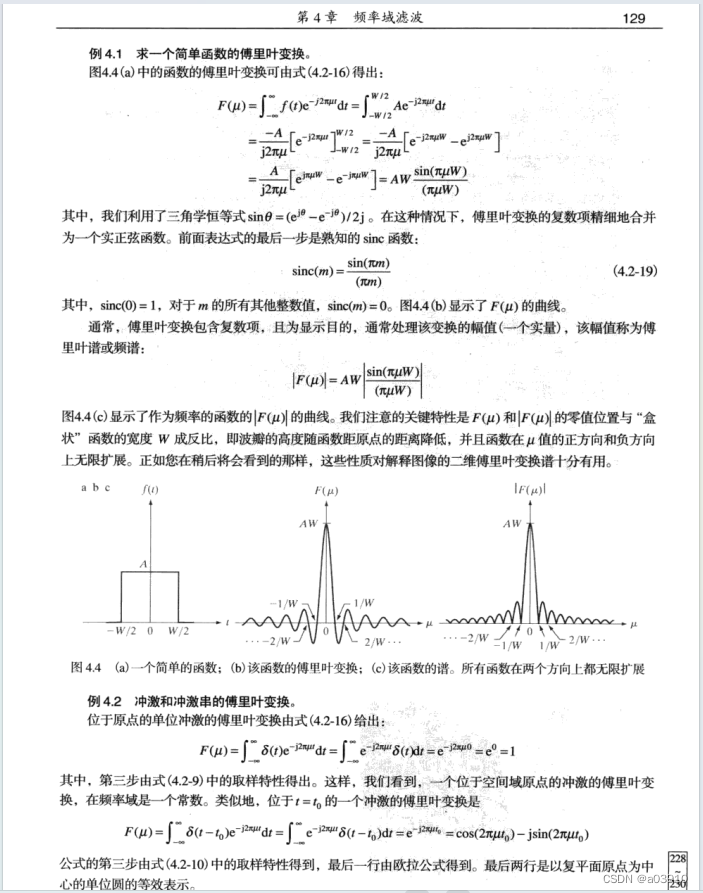
取样这里我需要说明一下，如何理解公式4.3-1。这个取样公式表示无限次取样，在间隔为 $\Delta$ T的时候。如何理解公式4.3-2呢？这个公式是在说fk是常数，而不是函数。

现在看公式4.3-5。这个公式中函数是以(1/ $\Delta$ T)为周期的周期函数吗？只要计算F~(u+1/ $\Delta$ T)就会发现确实是以1/ $\Delta$ T为周期。但是这个公式明显给出了一个问题，就是F~的每个函数值都是在F中取了无数个点相加的。在图4.6a,b,c,d中，恰好函数F在区间(-umax,uamx)之外为零。所有可以看作是有限和，理想的情况是在一个周期之内只有一个分量函数值，如图b,c。d是在重叠部分是两个函数值相加，这里正好是水平线段。

现在我来计算一下公式4.3-12吧。这本书是实话写的啰嗦，而且不清楚。

这里需要计算h(t)和f~(t)。

f~(t)书上就是公式4.3-1。

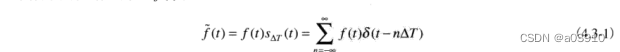
h(t)这个书上没有计算。但是书上计算了H(t)的傅里叶变换。

类比这个图4.4的计算过程，进行计算发现h(t)= $AW*\sin (\pi tW)/(\pi tW)$ ，其中由于W/2=umax, A=ΔT, 但是umax=1/(2ΔT)，所以w=1/ΔT。所以h(t)= $sinc (\pi t/\Delta T)$ 。

所以f(t)= $\sum_{n=-\infty }^{n=+\infty }\int_{-\infty}^{+\infty }h(\tau )*f(t-\tau)*\delta (t-\tau-n\Delta T)d\tau$ = $\sum_{n=-\infty }^{n=+\infty }h(t-n\Delta T)*f(n\Delta T)$ = $\sum_{n=-\infty }^{n=+\infty }h((t-n\Delta T)/\Delta T)*f(n\Delta T)$

这正是书上的公式4.3-12。上面的第二个等式是根据冲激的取样特性，这是定义的性质，在公式4.2-9和4.2-10给出了。

本来已经是无限次取样了在 $\Delta$ T的时间间隔中，用n表示，这里把取样函数傅里叶变换之后进行了有限次取样，在0-1/ $\Delta$ T的时间内取样M次。先看看公式4.4-2，这也是无限次累加了，fn是常数，书上说是函数是错误的。关键的问题是如果排除为零的可能，这里的无限次累加是不是有限次累加呢？但是我发现就是无限次累加的。

这样的话，公式4.4-4出现的就很突然，因为如果把fn看做是只有M个点离散函数，进行傅里叶变换，得到Fm确实就是公式4.4-4。根本不需要前面的那么多计算，书上做了这么多计算是为什么呢？我认为作者可能自己也不懂，胡乱拼接的。实际上算法导论中的傅里叶变换的定义更加合理，按照算法导论的内容理解公式4.4-4，更直观。（我很想贴算法导论的内容，但是已经超出了本书的范围，那就不管了，我只是提醒这里写错了，《算法导论 Tomas H.Cormen....》的内容写的不错。）

这篇关于傅里叶变换(书上居然写错了，作者不懂居然还能写这么多。)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！