本文主要是介绍使用统计学分析《鱿鱼游戏》中“玻璃垫脚石”的生存概率,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

来源:Deephub Imba本文约2600字,建议阅读8分钟
如果你要在鱿鱼游戏中玩玻璃垫脚石,你会选择那个数字?
《鱿鱼游戏》是最近很火的电影,在阅读本篇文章之前,我假设你已经看过这部剧集了。比赛中需要使用不同的策略才能获胜,比如第7集中的“玻璃垫脚石”引起了我的注意。这是一场至关重要的比赛,16 名玩家中只有 3 名幸存者。我认为这款游戏与其他游戏不同,因为从统计的角度来看,这是一款赌博游戏,玩家的行为并不能帮助他们获胜。现在让我们来使用数据来证明这一点。

不管你信不信其实每个玩家的命运几乎在他们选号时就已经确定了,而他们在游戏中的表现并没有多大关系。拥有运气也是一种超能力(例如海贼王中的巴基大神 ,一拳超人中的King)。但是对于我们普通人来说,了解一些统计知识就可以让我们在这样的游戏中生存。
在这篇文章中,我将讨论以下问题:
只有3名幸存者活下来了。如果再次玩游戏,是否有可能有更多(或更少的幸存者)?出现其他结果的概率是多少?
这个游戏的生存概率是3/16吗?生存概率与游戏顺序有什么关系?
如何根据猜对了多少玻璃来判断玩家是否是骗子?
如何在这场比赛中生存?
来自平行宇宙的游戏的其他结果
为了回答这些问题,我使用“生存分析”的思想进行了模拟。它是一种广泛用于分析死亡、疾病发生、康复等事件的统计分析[1],以计算受试者存活的概率。
进行生存分析的一种方法是通过模拟运行数千或数百万次实验,然后计算你感兴趣的生存概率。因为运行一个实验就像是在观察平行宇宙中会发生什么,您甚至可以从一个先知(如果存在先知)的视角来阅读从模拟结果中得到的悲伤或快乐的故事!
让我们先回顾游戏规则:所有玩家选择1到16之间的数字,然后他们将在限定时间内按照这个顺序过桥。桥牌上有18排玻璃,玩家需要从每排中挑选左边或右边的玻璃。如果他们选对了就可以继续走下去,否则就会从桥上掉下来死去。
为了简化模拟的问题,我需要做一些假设:
如果玩家没有死,他们会继续行走。
玩家随机选择玻璃(即猜对每一行的概率是0.5)——不允许作弊。
在模拟游戏中并不考虑时间效应(通过取消模拟中的时间限制对玩家表示一些怜悯,其实是简化了我们的计算)。
现在我们可以用Python建立的平行世界,给玩家另一个玩游戏的机会。我创建了一个Python函数来模拟游戏过程,计算生还者的数量,以及他们猜对了多少次。让我们看看运行游戏后得到的一些有趣结果:
平行宇宙A得到了类似结果
我们有 3 个幸存者但是与节目不同的是,玻璃专家(节目第14位玩家)初试失败!大部分玩家一试就没有猜对。

平行宇宙B是一个快乐故事
13名玩家在这个宇宙中幸存下来,玩家4猜对了9次!团队的英雄!但是猜对 9 次的概率是多少?这个玩家是作弊了吗?还是霸王色运气?我们稍后会在文中讨论这个问题。

平行宇宙C是悲伤的故事
这对于拥有 9 名幸存者的团队来说还不错。我说这很可悲是因为玩家4 猜对了 6 次,然后他就死了。4号玩家R.I.P。对团队贡献最大,但是还没没能活下来。

最有可能发生什么?

上面的结果告诉我们,每次运行结果都可能大不相同。我们可以根据幸存者的数量来计算每个不同结果的概率吗?当然可以!我们只需要多次运行实验(我在分析中运行了 100,000 次),然后我们可以根据模拟计算概率。
让我们看看这些概率:

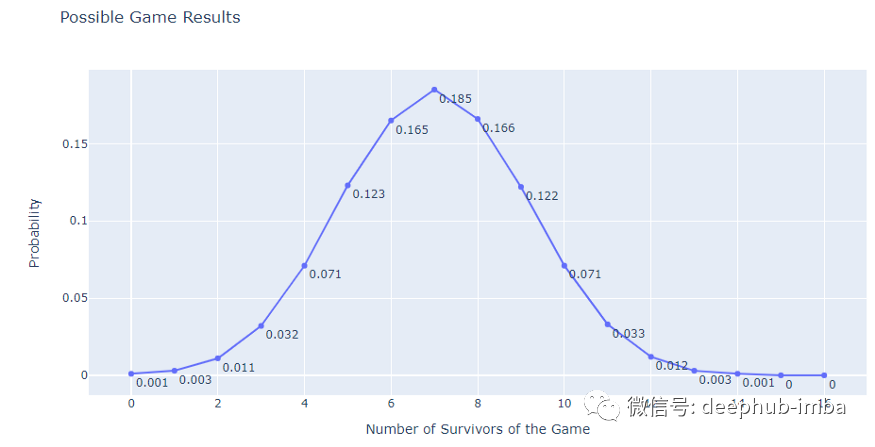
正如我们从上面看到的(正态分布对吧),这场比赛最有可能在最后有 7 名幸存者。几乎不可能没有幸存者(概率为 0.1%),或者整个团队的都是幸存者(概率为 0)。也就是说这个游戏注定有人要死去。
但是,我们也应该注意到,节目中的游戏比我们在这里模拟的要困难得多。比如:有时间限制。可以把人推到前面,试图改变游戏顺序,甚至作弊。但多亏了这些“人为因素”,这部剧看起来更精彩,也更关键,只有3名幸存者。
哪些玩家真的很幸运?
正如我在开头提到的,这是一个依赖顺序来玩的游戏。那么他们的生存机会如何随着顺序的的变化而变化吗?这是模拟输出:

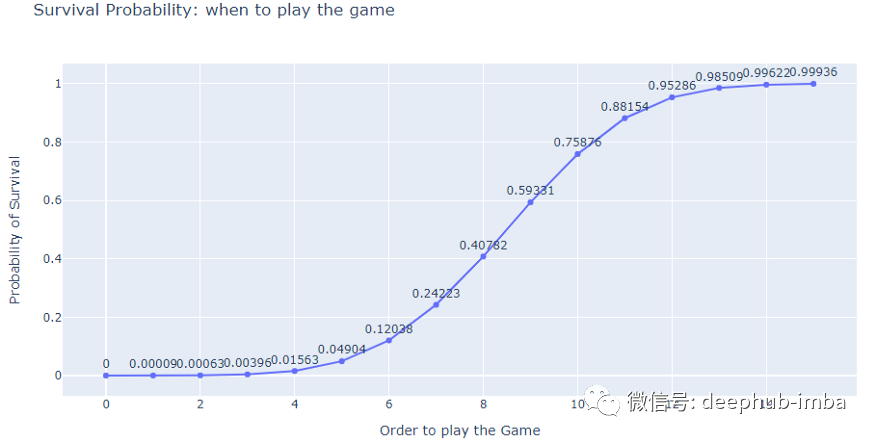
前 6 名玩家的生存机会不到 5%。而对于最后4名玩家(13-16号),他们可以在这场比赛中放松身心,生存机会超过95%。但是即使曹尚佑(№218)学了统计学,知道自己和前面的人都有可能活下来,我想他还是会选择当杀手,推那个可怜的家伙,因为是导演让推的。
如何判断玩家是否作弊?
“Everyone Is Equal While They Play This Game. Here, The Players Get To Play A Fair Game Under The Same Conditions. Those People Suffered From Inequality And Discrimination Out In The World, And We’re Giving Them The Last Chance To Fight Fair And Win.” — The Front Man[2]

如果一男(图片中的老家伙,No.001)参加了这场比赛并且他知道所有正确的步骤,你能说他知道一些事情而不是仅仅依靠运气吗?
我们可以使用一些基本的贝叶斯统计来解决这个问题。假设我们有:
赛前对一男的了解:我们相信他是真实玩家,有99%的几率,而他作弊的几率只有1%。
问题:在我们确信他作弊之前,他需要猜对多少次?
贝叶斯统计的解决方案:
1.让我们先假设他猜对了 5 次:
先验比率:作弊与非作弊是 1/99
问题:不作弊的概率为1/(2⁵)=1/32,作弊猜对5次的概率为1,所以似然比为1/(1/32)=32
后验比率 = 先验比率 * 似然比率 = 1/99 * 32 = 32/99
后验:作弊概率 = 32/(32+99) = ~24%。
2.现在假设他猜对了 10 次:
先验比率:作弊与非作弊是 1/99
问题:不作弊的概率为1/(2¹⁰)=1/1024,作弊者猜对10次的概率为1,所以似然比为1/(1/1024)=1024
后验比率 = 先验比率 * 似然比率 = 1/99 * 1024 = 1024/99
后验:作弊概率 = 1024/(1024+99) = ~91.2%。
正如我们从计算中看到的,如果玩家猜对了 10 次,我们将非常确定他是一个作弊者。概率为:91.2%。
作为玩家如何在这款游戏中生存?
最终解决方案:将您的幸运数字更改为更大的数字。
这是肯定的,从上面我们了解到生存的最好方法是获得最后一个数字:13-16 都是不错的选择(假设您不会被身后的玩家杀死)。
如果你运气不好,得到了 1-8 的数字,那么最好的生存机会就是说服其他 1-9 的玩家退出(根据规则,如果一半以上的人同意,游戏就可以停止)。那么如何说服他们放弃?说服前8名玩家并不难,因为最大的生存机会只有0.41。但是要说服机会为0.6的第9位玩家就很难了!我不知道节目的导演是否计算过这个数字(我个人觉得应该是算过了),但我想在这种情况下,9号玩家不会轻易被说服(假设他们都知道统计数据)。
最后本文的代码在这里:
https://github.com/mingjiezhao/squid_game_survival_analysis
引用:
[1] https://screenrant.com/squid-game-episode-7-game-bridge-rules-explained/
[2]https://en.wikipedia.org/wiki/Survival_analysis
[3] Squid game, Netflix
[4] https://screenrant.com/squid-game-netflix-bravest-characters/
作者:本篇文章是一个在Disney工作的的漂亮小姐姐 Mingjie Zhao撰写的,欢迎大家关注她的github
编辑:黄继彦
校对:林亦霖

这篇关于使用统计学分析《鱿鱼游戏》中“玻璃垫脚石”的生存概率的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




