本文主要是介绍【路径规划】基于六次多项式的多关节机器人避障路径规划,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近迷上了机械臂避障轨迹规划,因为之前一直做的都是无障碍物轨迹规划,所以这次想试一下有障碍物的,把避障算法用在我的SimMechanics机械臂上,看看效果咋样。以下定义不区分路径规划和轨迹规划。
by the way,本文实现的是全局静态避障,而非局部动态避障 : )
0. 任务目标
实现六关节机器人任务空间避障轨迹规划。
1. 思路分析
本人之前尝试过使用采样算法RRT来进行三维路径的避障和寻优,不过感觉步骤比较繁琐,而且很多文章都是到三次B样条曲线拟合完路径就结束了,最后也没说怎么保证末端执行器的速度、加速度平滑和各个关节运动的运动平滑。
鉴于此,本人放弃基于笛卡尔空间的避障轨迹规划,改做基于关节空间的避障轨迹规划。此方法相比于前个方法来说更加简便且不存在上述问题。
基于关节空间轨迹规划需要考虑的有:
- 碰撞检测
- 轨迹规划
- 遗传优化
2. 碰撞检测
多关节机器人碰撞检测和移动机器人不一样,其不仅需要考虑末端执行器的避障而且还需要考虑中间连杆的避障,这里采用包围盒的思想,将连杆视为圆柱体,将障碍物视为球体。
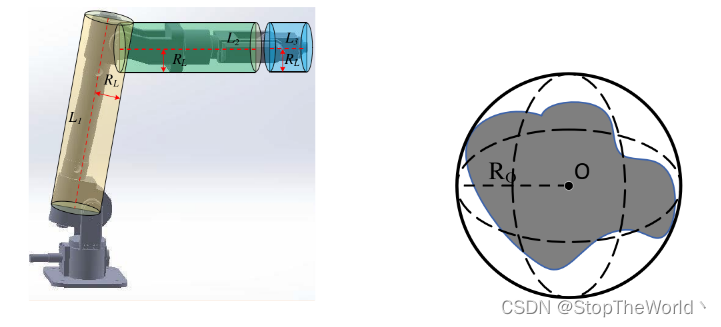
进一步地,根据多关节机器人的运动特性,其碰撞检测可以转化为由障碍物圆心到三个部分连杆中心线的距离d1、d2、d3。当d小于安全距离时即认为发生碰撞。
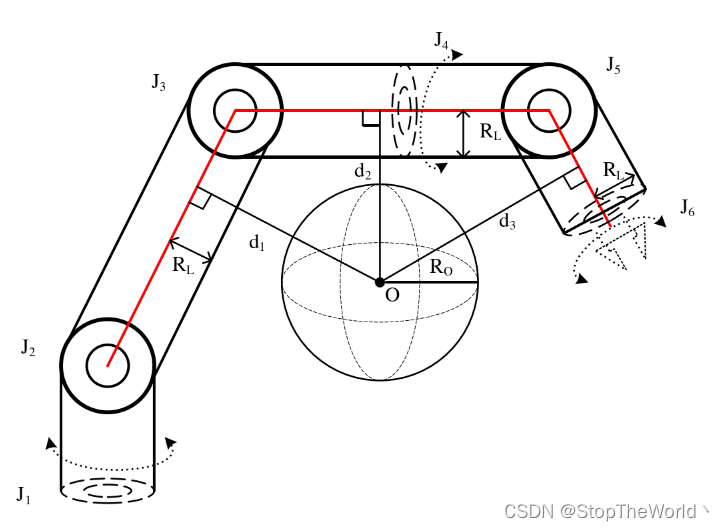
3. 轨迹规划
当确定关节始末角度、速度、加速度边界条件时,五次多项式关节空间轨迹规划只能确定出一条唯一的运动曲线,所以这里采用六次多项式来进行关节轨迹规划
θ t = c 0 + c 1 t + c 2 t 2 + c 3 t 3 + c 4 t 4 + c 5 t 5 + K t 6 \boldsymbol{\theta }_t=\boldsymbol{c}_0+\boldsymbol{c}_1t+\boldsymbol{c}_2t^2+\boldsymbol{c}_3t^3+\boldsymbol{c}_4t^4+\boldsymbol{c}_5t^5+\boldsymbol{K}t^6 θt=c0+c1t+c2t2+c3t3+c4t4+c5t5+Kt6其中, θ = [ θ 1 , θ 2 , θ 3 , θ 4 , θ 5 , θ 6 ] \boldsymbol{\theta }=\left[ \theta _1, \theta _2, \theta _3, \theta _4, \theta _5, \theta _6 \right] θ=[θ1,θ2,θ3,θ4,θ5,θ6],代表机械臂的六个关节角, K \boldsymbol{K} K 为可调参数, K = [ K 1 , K 2 , K 3 , K 4 , K 5 , K 6 ] \boldsymbol{K}=\left[ K_1, K_2, K_3, K_4, K_5, K_6 \right] K=[K1,K2,K3,K4,K5,K6],通过改变系数K即可改变关节运动轨迹。六次多项式依然能保证各关节角度、角速度、角加速度的连续平稳运动。
4. 遗传优化
现在的问题在于,如何能找到比较合适的K值,使得正运动学后的机器人末端执行器和连杆运动能够绕过障碍物,比较不错的方法是采用遗传算法,通过迭代找到最优值。为了方便,这里就采用我之前用过的JADE差分算法来进行寻优。
适应度函数的确定:遗传优化的目的是在机械臂全局避障的同时,减少不必要的运动,所以适应度函数分为三部分:碰撞检测结果 f c o f_{co} fco、六个关节的角度变化总和 f θ f_{\theta} fθ、末端执行器的运动轨迹长度 f L f_L fL。进而则有 f K = − f c o η 1 f θ + η 2 f L f_K=-\frac{f_{co}}{\eta _1f_{\theta}+\eta _2f_L} fK=−η1fθ+η2fLfco 基于此,可在关节空间中规划出一条无碰撞,同时运动学、轨迹长度、关节转动角度一起协同优化的理想运动轨迹。
5. 仿真验证
将多关节机器人初始位置设在零位q=[0,0,0,0,0,0]rad,此时末端执行器初始位置为T=[0.8201, 0.0391, 0.9483]m,将末端执行器终点位置设为X移动-0.1m,Y移动+0.4m,Z移动-0.4m,即[0.7201, 0.4391, 0.5483]m,通过逆解即可求得末端终点位置对应的各关节角度。
在机械臂的路径中设置球体障碍物,球体中心坐标设为[0.8, 0.2, 0.8]m,半径设为0.1m,六个关节的角速度、角加速度边界均设置为0。此外,设机械臂运行时间为5s,插值点个数为50,即每段插值点间的运行时间为0.1s。
仿真结果:
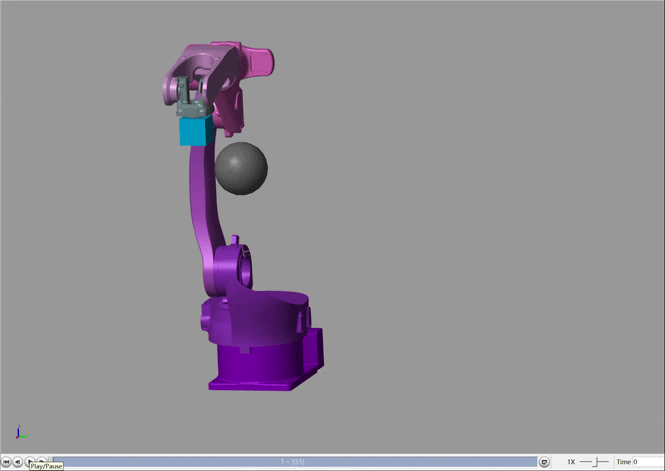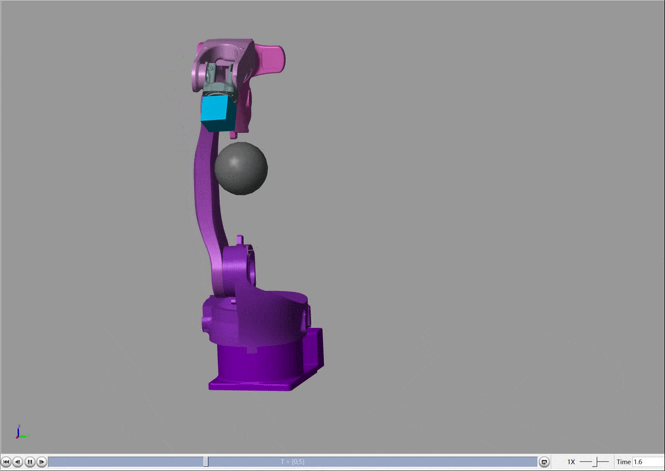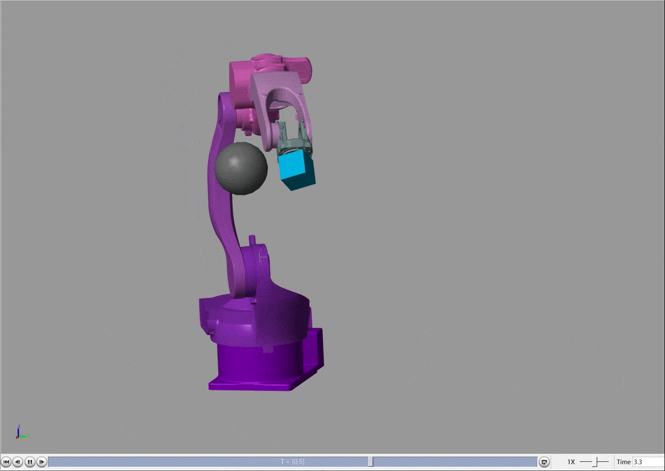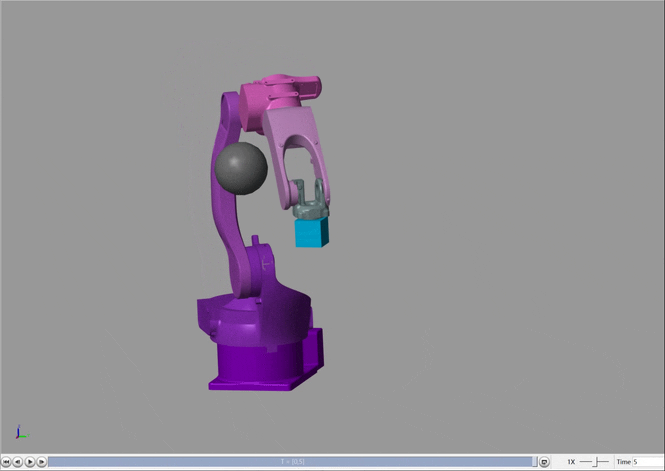
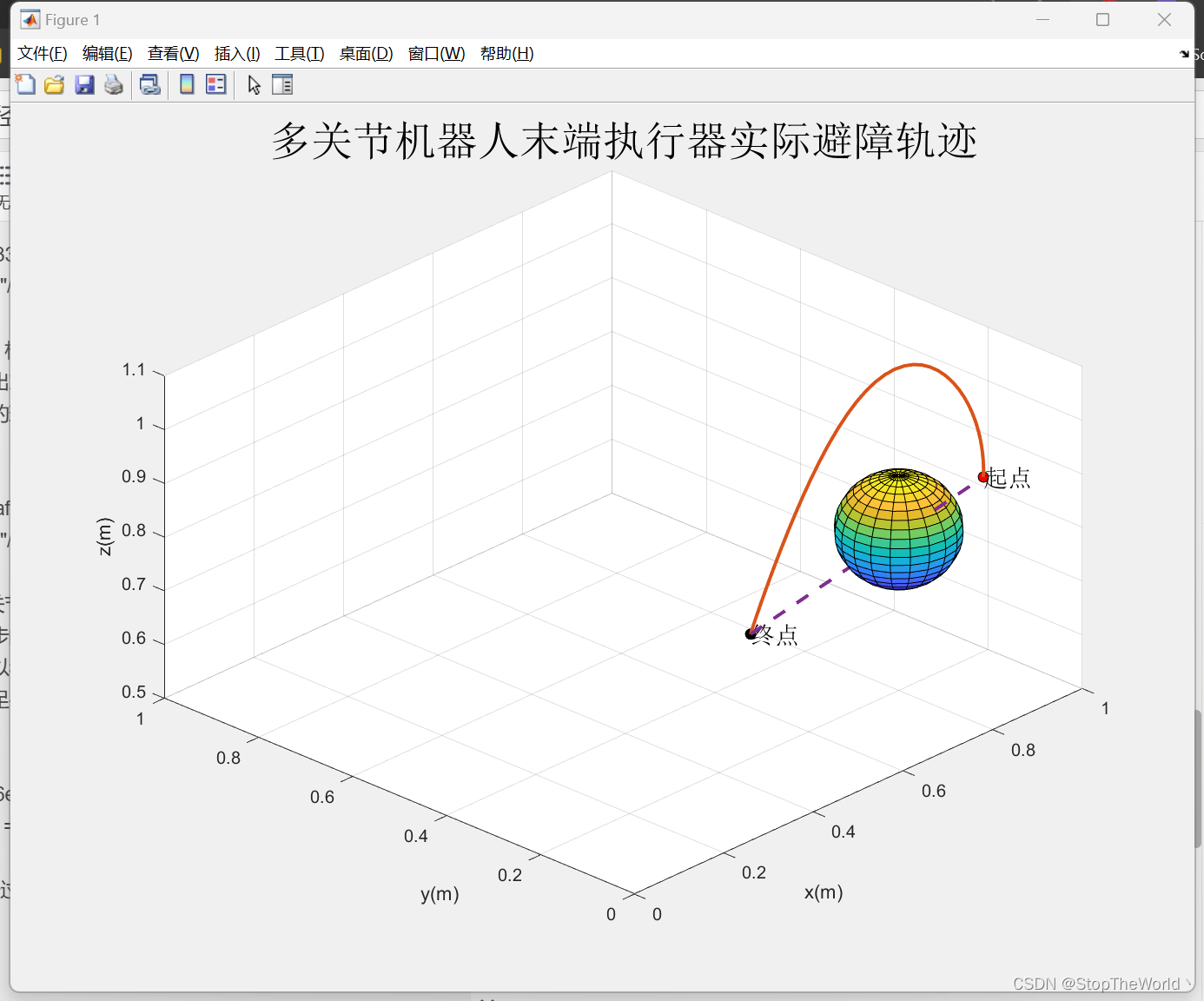
可以看出,机械臂在运动过程中发生了很明显的避让现象,为了更明显的观察,绘制出末端执行器的三维运动轨迹,红色为实际运动轨迹,虚线为无障碍物时的理想运动轨迹。
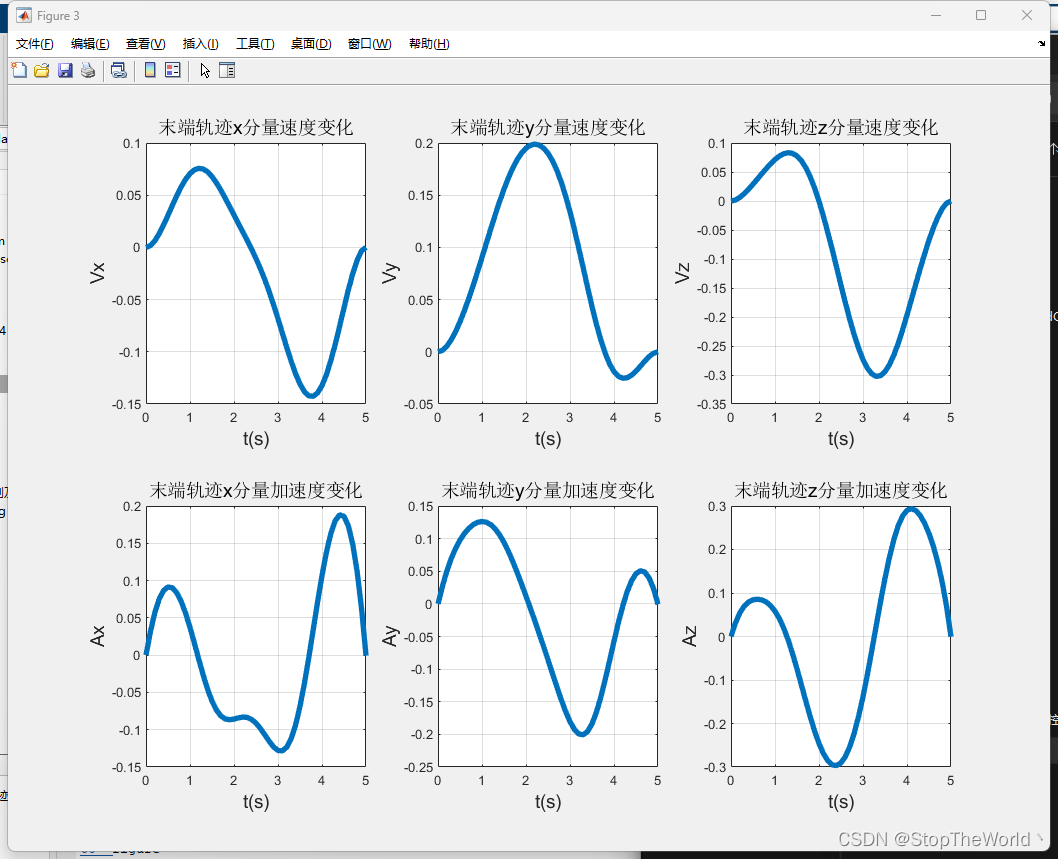
由于各个关节的运动曲线为六次多项式,所以关节角速度、角加速度满足平滑条件,进一步的,绘制出末端执行器在XYZ方向分量上的速度、加速度曲线,可以看出,机械臂末端执行器的速度、加速度曲线均为连续平滑曲线,满足平稳运动的条件。
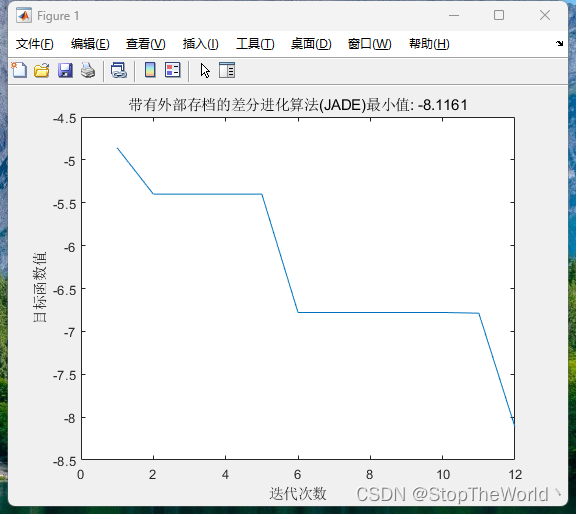
JADE寻优迭代图,在经过12次迭代后,迭代出了K的较优值和较小的适应度值。
6. 总结
基于以上结论,成功的实现了多关节机器人避障路径规划,虽然没有找到一条最优路径,但已经找到了一条较优路径,且同时具备安全、稳定、高效的作用,有了以上的各个关节角度曲线,后续设计轨迹跟踪控制器即可完成机械臂高精度的轨迹跟踪。
本次实验圆满完成 : )
这篇关于【路径规划】基于六次多项式的多关节机器人避障路径规划的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





