Stanford CS231N

本文主要是介绍Stanford CS231N，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 introduction to convolutional neural network

image segmentation:
object recognition
face detection
SIFT: some features tend to remain diagnostic and invariant to changes
PASCAL visual object challenge
ImageNet:22k categories and 14M images: ImageNet large-scale visual recogniton challenge
http://cs231n.github.io/gec-tutorial

2 Image classification pipeline

challenge：
semantic gap（语义）
viewpoint variation
illumination
deformation
occlusion
intraclass variation

data-driven approach

1. collect a dataset of images and labels
2. use machine learning to train a classifier
3. evaluate

CIFAR10
10 classes
50,000 training images
10,000 testing images
each image is 32323

2.1 nearest neighbors classifier/KNN

时间复杂度：
Train: O(1)
predict: O(N)
改进：KNN: K-Nearest Neighbors，按照majority vote原则
缺点：
very slow ate test time
distance are not informative

距离
Manhattan distance：正方形
Euclidean distance：圆形

超参数hyperparameter: depend on problem and data
Setting Hyperparameters: cross-validation

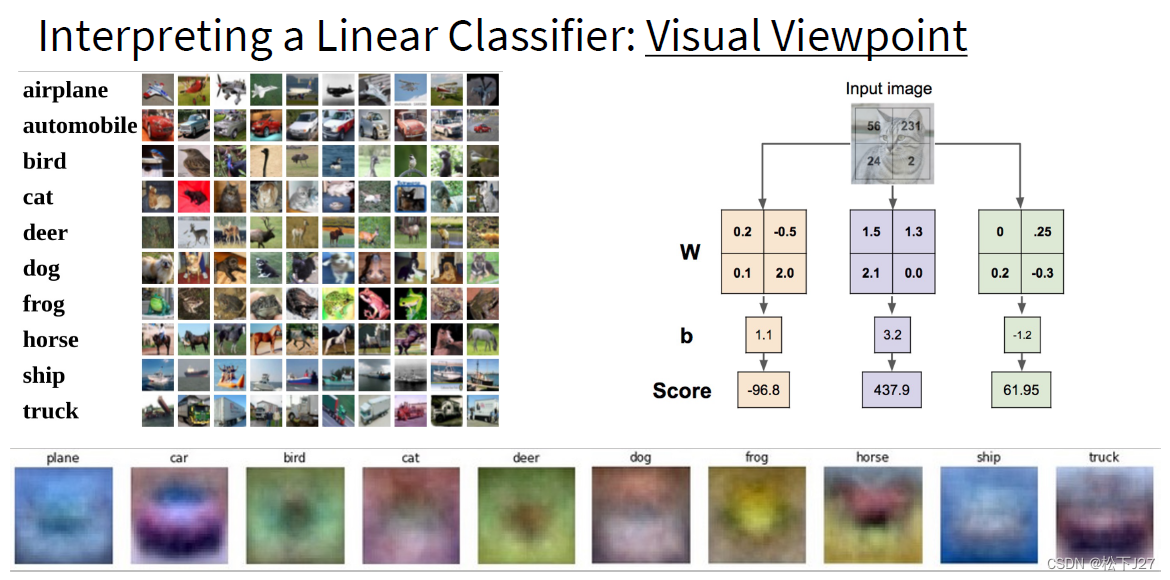
2.2 Linear classification

$$f(x,W)=Wx+b$$
http://cs231n.github.io/assignments0217

3 loss function and optimization

3.1 loss function of multclass SVM

cs229会讲SVM
$$L_i=\sum _{j̸=y_i}\{\begin{array}{cc}0& if{s}_{y_i}>s_j+1\\ s_j-s_{y_i}+1& \end{array}$$
$$=\sum _{j̸=y_i}max(0,s_j-s_{y_i}+1)$$
where $s_{y_i}$is the predicted score of true category
损失函数最小值是0，最大值是正无穷

3.2 Softmax Classifier(Multinomial Logistic Regression)

$$L_i=-logP(Y=k|X=x_i)=-log\frac{e^{s_k}}{{\sum }_j{e}^{s_j}}$$
希望$P(Y=k|X=x_i)$接近1,所以希望$-logP(=k|X=x_i)$接近0
损失函数都最大值是正无穷，最小值是0

3.3 optimization

• random search: 最愚蠢最简单的做法
• 梯度下降：便利所有训练集计算得到梯度

while True:weights_grad=evaluate_gradient(loos_fun,data,weights)weights+=-step_size*weights_grad

其中step_size就是学习率

• 随机梯度下降：用一部分(x,y)来预估gradient，称为一个batch，以此减少计算量

3.4 Image Features

分类器的输入最好是图像的特征，而不是像素点
坐标变换、有向梯度直方图、词袋

4 Introduction to neural networks

4.1 backforward propagation

patterns in back gradient
max gate: 只传给最大的那个值
gradients add at branches
对于graph structure要有forward()和backward()

4.2 neural network

一个简单的2-layer neural network: $f=W_{2}max(0,W_{1}x)$

5 convolutional neural networks

5.1 convolutional layer

5.2 pooling layer

downsampling

• max pooling
• average pooling

6 training neual network 1

6.1 activation function

6.2 weight initialization

W初始化太大：激活函数会饱和
W初始化太小：输出太小，约等于0
最好的情况是每一层都是高斯分布的

6.3 batch normalization

usually inserted after fully connected or convolutional layers, and before nonlinearity
$$x^{\prime }=\frac{x-E[x]}{\sqrt{var[x]}}$$

7 training neual network 2

7.1 hyperparameter search

7.2 fancier opitimization

noise can be averaged

这篇关于Stanford CS231N的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---