Kosaraju算法---求解强连通分量

本文主要是介绍Kosaraju算法---求解强连通分量，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

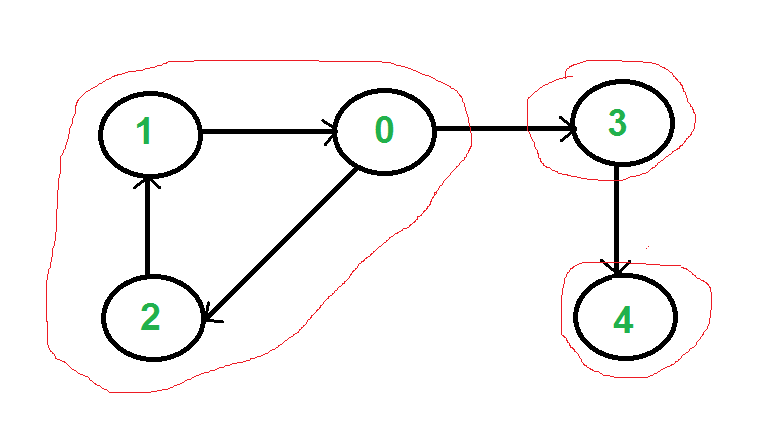
有向图强连通分量在有向图G中，如果两个顶点Vi，Vj间（Vi>Vj）有一条从Vi到Vj的有向路径，同时还有一条从Vi到Vj的有向路径，则称这两个顶点强。连通（strongly connected），如果有向图G中的任意两个顶点都强连通，则称G是一个强连通图。

Kosaraju算法、Tarjan算法、Gabow算法皆为寻找有向图强连通分量的有效算法。但是在Tarjan 算法和 Gabow 算法的过程中，只需要进行一次的深度优先搜索，而Kosaraju算法需要两次DFS，因而相对 Kosaraju 算法较有效率。这些算法可简称为SSC(strongly connected components)算法;

Kosaraju 算法即为算法导论一书给出的算法，比较直观和易懂。这个算法可以说是最容易理解，最通用的算法，其比较关键的部分是同时应用了原图G和反图GT。 它利用了有向图的这样一个性质，一个图和他的transpose graph(边全部反向)具有相同的强连通分量！

## 算法步骤 ##

1) 创建一个空的栈 ‘S’ ，然后对图做DFS遍历. 在顶点访问完成后加入栈中。访问完成是说回溯返回时，而不是第一次发现该节点时。fillOrder()函数
2) 得到图转置，即将所有边反向。
3) 从S中依次弹出每个顶点，设为 ‘v’. 将v看做遍历的源点 (调用 DFSUtil(v)). 做第二次DFS遍历，可以找到以v为起点的强连通分量，打印出即可。

## 代码 ##

    #include<iostream>
#include<list>
#include<stack>
using namespace  std;class  Graph
{int V;  //顶点个数list<int>  *adj;   //邻接表void fillOrder(int V, bool visited[], stack<int> &stack);//最晚完成的遍历顶点放在栈顶void DFSUtil(int v, bool visited[]);//DFS打印以V为起点的边
public:Graph(int V);void addEdge(int v, int w);void printSCCs();//打印所有的连通分量Graph getTranspose();//得到当前图的转置图
};Graph::Graph(int V)
{this->V = V;adj = new list<int>[V];
}void Graph::DFSUtil(int v, bool visited[])
{visited[v] = true;cout << v << " ";list<int>::iterator i;for (i = adj[v].begin(); i != adj[v].end();i++){if (!visited[*i]){DFSUtil(*i, visited);}}
}Graph Graph::getTranspose()
{Graph g(V);for (int v = 0; v < V;v++){list<int>::iterator i;for (i = adj[v].begin(); i != adj[v].end();++i){g.adj[*i].push_back(v);}}return g;
}void Graph::addEdge(int v, int w)
{adj[v].push_back(w);
}void Graph::fillOrder(int v, bool visited[], stack<int> &stack)
{visited[v] = true;list<int>::iterator i;for (i = adj[v].begin(); i != adj[v].end();i++){if (!visited[*i]){fillOrder(*i, visited, stack);}}stack.push(v);
}void Graph::printSCCs()
{stack<int> stack;bool *visited = new bool[V];for (int i = 0; i < V;i++){visited[i] = false;}for (int i = 0; i < V;i++){if (visited[i]==false){fillOrder(i, visited, stack);//根据完成时间压入栈中，而栈顶是完成时间最晚的顶点；}}//下面，我们来创建转置图Graph gr = getTranspose();//准备第二次DFSfor (int i = 0; i < V;i++){visited[i] = false;}while (stack.empty()==false){int v = stack.top();stack.pop();//打印以v为起点的强连通分量if (visited[v]==false){gr.DFSUtil(v, visited);cout << endl;}}
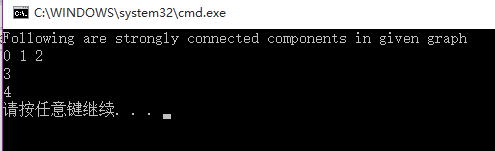
}//测试程序int main() {// 创建图Graph g(5);g.addEdge(1, 0);g.addEdge(0, 2);g.addEdge(2, 1);g.addEdge(0, 3);g.addEdge(3, 4);cout << "Following are strongly connected components in given graph \n";g.printSCCs();return 0;}

这篇关于Kosaraju算法---求解强连通分量的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---