kosaraju专题
图论 求有向图的所有强连通分量 kosaraju算法
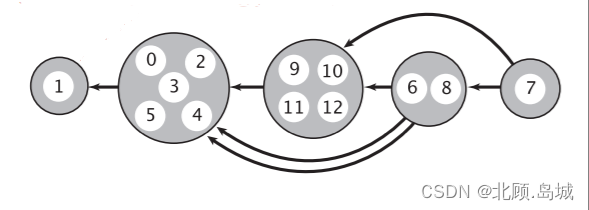
一、问题 如何找到有向图(a)中的所有强连通分量,如图(b) 二、kosaraju算法 Kosaraju的算法(又称为–Sharir Kosaraju算法)是一个线性时间(linear time)算法找到的有向图的强连通分量。 1. 原理 它利用了一个事实,逆图(与各边方向相同的图形反转, transpose graph)有相同的强连通分量的原始图。 2. 逆图
强连通分量Kosaraju、Tarjan【模板】
强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量。 把一个图变为一个强连通图需要添加边数:先求出原图的强连通分量,缩点后变为有向无环图,计算新图入度为0的点的个数SumIn和出度为0的点的个数SumOut
hdu1269 有向图 强连通分量 kosaraju 算法
迷宫城堡 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 4943 Accepted Submission(s): 2175 Problem Description 为了训练小希的方向感,Gardon建立了一座大城堡,里面有
Kosaraju算法---求解强连通分量
有向图强连通分量在有向图G中,如果两个顶点Vi,Vj间(Vi>Vj)有一条从Vi到Vj的有向路径,同时还有一条从Vi到Vj的有向路径,则称这两个顶点强。连通(strongly connected),如果有向图G中的任意两个顶点都强连通,则称G是一个强连通图。 Kosaraju算法、Tarjan算法、Gabow算法皆为寻找有向图强连通分量的有效算法。但是在Tarjan 算法和 Gabow 算法
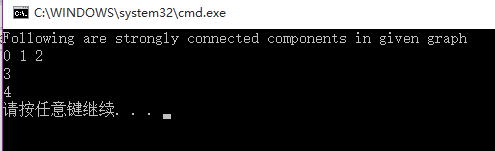
[ACM] POJ 2186 Popular Cows (强连通分量,Kosaraju算法知识整理)
首先是一些知识整理:来源于网络: 以下转载于:http://blog.sina.com.cn/s/blog_4dff87120100r58c.html Kosaraju算法是求解有向图强连通分量(strong connectedcomponent)的三个著名算法之一,能在线性时间求解出一个图的强分量。 什么是强连通分量?在这之前先定义一个强连通性(strong connectivi
强连通分量——Kosaraju算法
①随意选取一个结点开始深搜,当搜索完子树时将它压到栈中 ②将原图转置(边的方向变成与原来相反),从栈顶节点再进行深搜,每次深搜结束所得的节点就是一个强连通分量 <span style="font-size:14px;">#include<stdio.h>#include<string.h>#include<stack>#include<vector>#include<iost
【LeetCode题目拓展】第207题 课程表 拓展(拓扑排序、Tarjan算法、Kosaraju算法)
文章目录 一、拓扑排序题目二、题目拓展1. 思路分析2. tarjan算法3. kosaraju算法 一、拓扑排序题目 最近在看一个算法课程的时候看到了一个比较好玩的题目的扩展,它的原题如下: 对应的LeetCode题目为 207. 课程表 这个题目本身来说比较简单,就是一道标准的拓扑排序题目,解法代码如下: import java.util.ArrayList;im


![[ACM] POJ 2186 Popular Cows (强连通分量,Kosaraju算法知识整理)](https://img-blog.csdn.net/20140925160516009)