[ACM] POJ 2186 Popular Cows (强连通分量，Kosaraju算法知识整理）

本文主要是介绍[ACM] POJ 2186 Popular Cows (强连通分量，Kosaraju算法知识整理），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

首先是一些知识整理：来源于网络：

以下转载于：http://blog.sina.com.cn/s/blog_4dff87120100r58c.html

Kosaraju算法是求解有向图强连通分量（strong connectedcomponent）的三个著名算法之一，能在线性时间求解出一个图的强分量。

什么是强连通分量？在这之前先定义一个强连通性（strong connectivity）的概念：有向图中，如果一个顶点s到t有一条路径，t到s也有一条路径，即s与t互相可达，那么我们说s与t是强连通的。那么在有向图中，由互相强连通的顶点构成的分量，称作强连通分量。

首先说一些离散数学相关的结论，由强连通性的概念可以发现，这是一个等价关系。

证明：

一，按照有向图的约定，每个顶点都有到达自身的路径，即自环，即任意顶点s到s可达，满足自反性；

二，如果s与t是强连通的，则s到t存在路径，t到s存在路径，显然t与s也是强连通的，满足对称性；

三，如果r与s强连通，s与t强连通，则r与s互相可达，s与t互相可达，显然r与t也互相可达，满足传递性。

因此，强连通关系可导出一个等价类，这就是强连通分量。进一步的利用这结论可以知道，两个强连通分量之间木有交集（这个结论很重要）。事实上，图论与离散数学中的关系有非常密切的……关系。

以下转载于：http://blog.csdn.net/dm_vincent/article/details/8554244

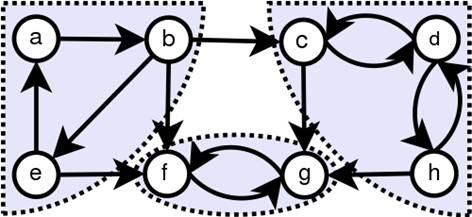
以上用虚线围绕的部分就是一个强连通分量，因此上图中总共含有三个。

对于一个强连通分量中的任意一对顶点(u，v)，都能够保证分量中存在路径使得u->v，v->u

比如上图中由a，b，e这三个顶点构成的分量中，任意两个顶点间都存在路径可达。

顺便也介绍一下有关“缩点”的概念：

由于强连通分量的特殊性，在一些实际应用中，会将每个强连通分量看成一个点，然后进行处理。这样做主要是为了降低图的复杂度，特别是在强连通分量规模大、数量多的情况中，利用“缩点”能大幅度降低图的复杂度。

缩点后得到的图，必定是DAG。用反正能够很方便的进行证明：因为若图中含有环路，即意味着至少有两个点彼此可达，那么按照强连通分量的定义，这两个点应该属于一个分量中，因而在缩点发生后，会被一个点所代表。由此推导出矛盾。比如，对上图进行缩点处理，最后的结果就是：

设(a，b，c) -> a'，(f，g) -> b'，(c，d，h) -> c'

因此最后的图就可以表示为：

下面对这个算法的正确性进行证明：(如果没有兴趣，可以直接略过 ：D)

证明的目标，就是最后一步 --- 每一颗搜索树代表的就是一个强连通分量

证明：设在图G^R中，调用DFS(s)能够到达顶点v，那么顶点s和v是强连通的。

两个顶点如果是强连通的，那么彼此之间都有一条路径可达，因为DFS(s)能够达到顶点v，因此从s到v的路径必然存在。现在关键就是需要证明在G^R中从v到s也是存在一条路径的，也就是要证明在G中存在s到v的一条路径。

而之所以DFS(s)能够在DFS(v)之前被调用，是因为在对G获取ReversePost-Order序列时，s出现在v之前，这也就意味着，v是在s之前加入该序列的(因为该序列使用栈作为数据结构，先加入的反而会在序列的后面)。因此根据DFS调用的递归性质，DFS(v)应该在DFS(s)之前返回，而有两种情形满足该条件：

1.            DFS(v)START -> DFS(v) END -> DFS(s) START -> DFS(s) END

2.            DFS(s)START -> DFS(v) START -> DFS(v) END -> DFS(s) END

是因为而根据目前的已知条件，G^R中存在一条s到v的路径，即意味着G中存在一条v到s的路径，而在第一种情形下，调用DFS(v)却没能在它返回前递归调用DFS(s)，这是和G中存在v到s的路径相矛盾的，因此不可取。故情形二为唯一符合逻辑的调用过程。而根据DFS(s) START -> DFS(v) START可以推导出从s到v存在一条路径。

所以从s到v以及v到s都有路径可达，证明完毕。

以下转载于：http://blog.csdn.net/michealtx/article/details/8233814

这个算法网上很多介绍，但大多都很相似，着重介绍算法实现而没有证明或者容易理解的解释。我说下自己对kosaraju算法的理解思路。这个算法名字我不会读，搜了半天看到本尊，发现他长得像印度人，也就释然了。回正题。kosaraju算法用来求一个有向图的所有强连通分量，算法很简单，但是理解起来有点麻烦，我是这么觉得。但是跟无向图的连通分量求法结合起来，就非常容易理解了。所以理解这个Korasaju算法的前提是你理解无向图所有连通分量的算法，这个算法相当图森破。
先看无向图的连通分量求法，其实无向图的连通分量就都是强连通分量。无向图的强连通分量就是用DFS算法顺序遍历邻接表时顺道干点小动作，写下代码更直观一些：

#define maxN 1024  
int marked[maxN];//用于记录某个点是否被访问过，0为没有被临幸过，1为被临幸过  
int id[maxN];//记录每个点所属的连通分量  
int count;//记录连通分量总数目  
void cc(graph *g){  int i;  memset(marked,0,sizeof(marked));  memset(id,0,sizeof(id));  count=0;  for(i=0;i<g->V;i++){//之所以这里用循环就是因为g指向的无向图可能不是一个连通图，而是由多个连同分量组成  if(!marked[i]){dfs(g,i); count++;}  }  
}  void dfs(graph *g,int v){  graphNode *t;  marked[v]=1;  id[v]=count;  t=g->adjlist[v].next;//t指向v的邻接点  while(t){  if(!marked[t->key]){dfs(g,t->key);}//这里是重点，就是你发现v到t->key有路径就把它算到跟自己在一个连通分量里了，这里有一个隐性前提，就是你提前知道t->key一定可以到v，所以你发现v可以到t->key的时候，你毫不犹豫把它算为跟自己一伙儿的了。Korasaju算法不同书上有不同的表述，区别是先遍历图g还是先遍历图g的逆向图，这只是顺序的区别。我把我看得版本完整说一下：（1）先DFS遍历图g的逆向图，记录遍历的逆后序。（什么叫逆后序？逆后序就是DFS时后序的逆序，注意逆后序不一定为DFS的前序。DFS前序为，访问某个顶点前，把它push进队列。DFS后序为访问完某个顶点后才把它push进队列。而DFS逆后序为访问完某个顶点后把它push进一个栈中。当DFS遍历完整个图后，后序队列的输出与逆后序栈的输出正好相反。）（2）然后按着图g逆向图的DFS遍历的逆后序序列遍历图g求所有的强连通分量，这一步的过程跟无向图求所有连通分量的算法一模一样！按着这里说的遍历顺序重复无向图求所有连通分量的步骤求出来的就是有向图的所有强连通分量，为什么呢？因为我们完成第一步后，按着第一步得到的逆后序要对有向图g进行DFS遍历的前一刻，前面这段过程就相当于我们完成了对这幅有向图g一个加工，把它加工成了一个无向图！也就是说，这个加工实现了我注释开头提到的那个隐性前提。所以后面按着无向图求所有连通分量的步骤求出来的就是有向图g的所有强连通分量。举个例子，比如有向图3->5->4->3，它的逆向图为3->4->5->3（你最好在纸上画下，就是个三角循环图），从逆向图的顶点3开始DFS，得到的逆后续为3，4,5 。按着这个顺序对原图进行DFS，DFS(3)时遇到5，则5肯定跟3在一个强连通分量中（为什么？因为我们逆向图DFS(5)时肯定能到达3，这就是隐形前提。所以正向图DFS(3)遇到5时，我们毫不犹豫把它算到自己一个强连通分量中。）  t=t->next;  }  
}  

上面这个还不太懂。

Procedure Stringly_Connected_Components(G)

Begin

       1.深度优先遍历G，算出每个节点u的结束时间ord[u],（给每个节点编号）起点如何选择无所谓。

       2.深度优先遍历G的转置图GT，选择遍历的起点时，按照节点的结束时间从大到小进行。遍历的过程中，一边遍历，一边给节点做分类标记（相当于染色，一遍DFS遍历到的所有节点染成相同的颜色，每找到一个新的起点，分类标记值就加1（一次新的DFS，clor++）.

       3.第2步中产生的标记值相同的节点构成深度优先森林中的一棵树（color值相同的节点组成了强连通分量），也即为一个强连通分量。

下面开始本题的部分：

Description

Input

Output

Sample Input

3 3
1 2
2 1
2 3

Sample Output

1

Hint

Source

题意为：给定一个有向图，求有多少定点是由任何顶点出发都可达的。

用到的定理：

有向无环图中唯一出度为0的点，一定可以由任何点出发均可达（由于无环，所以从任何点出发往前走，必然终止于一个出度为0的点）.

所以用kosaraju算法求出所有的强连通分量，然后进行缩点，转换成一个DAG图，然后找强连通分量出度为0的那个，如果有多个，则输出0，如果只有一个，就输出该强连通分量所包含的顶点个数。

代码：

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <vector>
using namespace std;
const int maxn=10010;
vector<int>g[maxn],gre[maxn];//存储正向图和逆图
int ord[maxn];//正向搜索，顶点的编号
bool vis[maxn];
int out[maxn];//转化为DAG以后的每个缩点的出度
int belong[maxn];//当前顶点属于哪个集合，相当于染色，当前顶点被染成了什么颜色
int ans[maxn];//每种颜色包括多少顶点,也就是强联通分量的个数
int color;//代表不同的颜色
int no;//正向搜索排序的编号
int n,m;//顶点数和边数void dfs1(int u)//从当前u顶点开始DFS
{vis[u]=1;for(int i=0;i<g[u].size();i++){int v=g[u][i];if(!vis[v])dfs1(v);}ord[no++]=u;//为每个顶点编号
}void dfs2(int u)
{vis[u]=1;belong[u]=color;//当前顶点u被染成了colorfor(int i=0;i<gre[u].size();i++){int v=gre[u][i];if(!vis[v]){ans[color]++;dfs2(v);}}
}void kosaraju()
{color=1,no=1;for(int i=1;i<=n;i++)ans[i]=1;memset(out,0,sizeof(out));memset(vis,0,sizeof(vis));for(int i=1;i<=n;i++)if(!vis[i])dfs1(i);memset(vis,0,sizeof(vis));for(int i=no-1;i>=1;i--)//编好号以后，从排号最大的开始搜索{int v=ord[i];if(!vis[v]){dfs2(v);color++;}}//构造DAGfor(int i=1;i<=n;i++){for(int j=0;j<g[i].size();j++){if(belong[i]==belong[g[i][j]])continue;out[belong[i]]++;}}//查找每种颜色出度为0的点或缩点，out[i]，代表第i种颜色的点或缩点的出度，出度为0唯一，输出该颜色集合中点的个数ans[i]，否则输出0int ret=0;int cnt=0;for(int i=1;i<color;i++){if(!out[i]){cnt++;ret=ans[i];}if(cnt==2)//这两个if不能写颠倒，切记啊!{ret=0;break;}}printf("%d\n",ret);
}int main()
{while(scanf("%d%d",&n,&m)!=EOF){int u,v;for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);g[u].push_back(v);gre[v].push_back(u);}kosaraju();}return 0;
}

这篇关于[ACM] POJ 2186 Popular Cows (强连通分量，Kosaraju算法知识整理）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！