本文主要是介绍数学建模-最优包衣厚度终点判别法(主成分分析),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
💞💞 前言
hello hello~ ,这里是viperrrrrrr~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹
💥个人主页:viperrrrrrr的博客
💥 欢迎学习数学建模算法、大数据、前端等知识,让我们一起向目标进发!
基于近红外光谱的肠溶片最优包衣厚度终点判别法
包衣是将片剂的外表面均匀地包裹上一层衣膜的过程,旨在控制药物在胃肠道中的释放部位和速度,遮盖苦味或不良气味,防潮、避光,改善外观等。然而,包衣膜太薄或太厚都不利于药效,并且包衣终点的判断方法目前存在一定的难度。近红外光谱技术(NIRS)是一种高效、无需试剂、无污染的分析方法,通过近红外光谱仪、化学计量学软件和应用模型,能快速、简便地实现多组分检测。为实现包衣终点的准确判断,对数据进行分析并完成以下问题:
问题一:对药品在不同包衣时间段包衣片剂的近红外光谱进行特征峰提取,选择具有有效信息的波长片段,即波长选择。
问题二:分析药品包衣厚度分类规律,建立合适的模型对药品包衣不同厚度进行划分,给出方法及结果,并进行灵敏度分析。
问题三:对于不同的包衣厚度,通过建立模型分析包衣之间的关联性,判别出最优的包衣厚度。
我们本次主要解决问题一
问题一
包衣是将片剂均匀地包裹衣膜,用于控制药物释放、遮盖苦味等。然而,包衣膜太薄或太厚都不利于药效,并且包衣终点的判断方法目前存在一定的难度。而近红外光谱技术是一种无污染、快速、多组分检测的分析方法,它适用于包衣终点的确定。本文基于一批现有的红外光谱相关数据,建立主成分分析、聚类分析、Bayes判别等模型和梯度下降算法,实现了片剂包衣最佳终点的判断。建立了主成分分析模型进行特征峰选取,利用主成分分析中广泛使用的降维技术,通过线性变换将高维数据集转化为低维数据集,同时保留数据集中的主要信息。由于不同的特征会有不同的量纲,这可能会影响到模型的性能,因此在应用PCA之前,通常需要对数据进行数据预处理。列出协方差矩阵反映数据集中各特征之间相关性的矩阵。通过求解协方差矩阵的特征向量和特征值,可以得到数据集的主成分。这些主成分是原始特征空间中的线性变换,它们是新的、相互独立的、能够捕捉到数据变动的最大方差的向量。
首先,通过滑动平均滤波法对附件数据进行平滑处理,即滤波。基于附件数据,由图(1)可见原始波长噪音数据较多,会影响最终数据结果[1]。使用5倍滑动滤波进行降噪处理后,由图(2)可见,成功过滤了部分噪声数据,使光谱变得更加平滑。
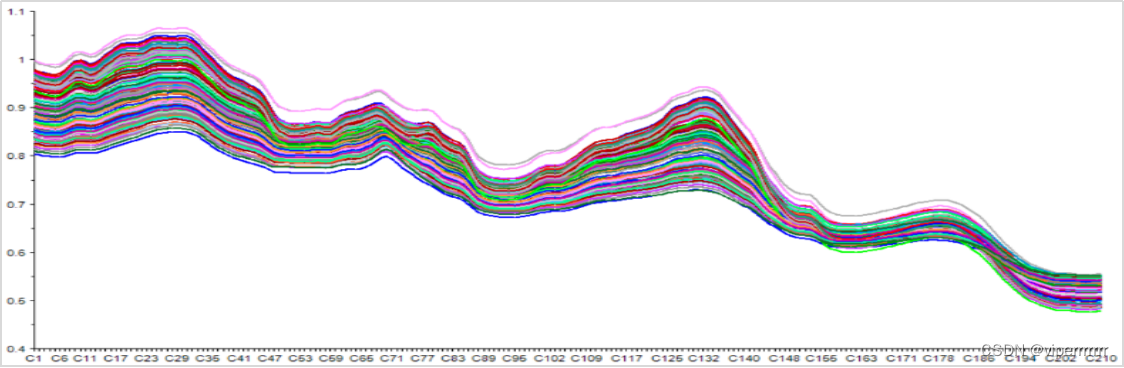
图1 原始数据图
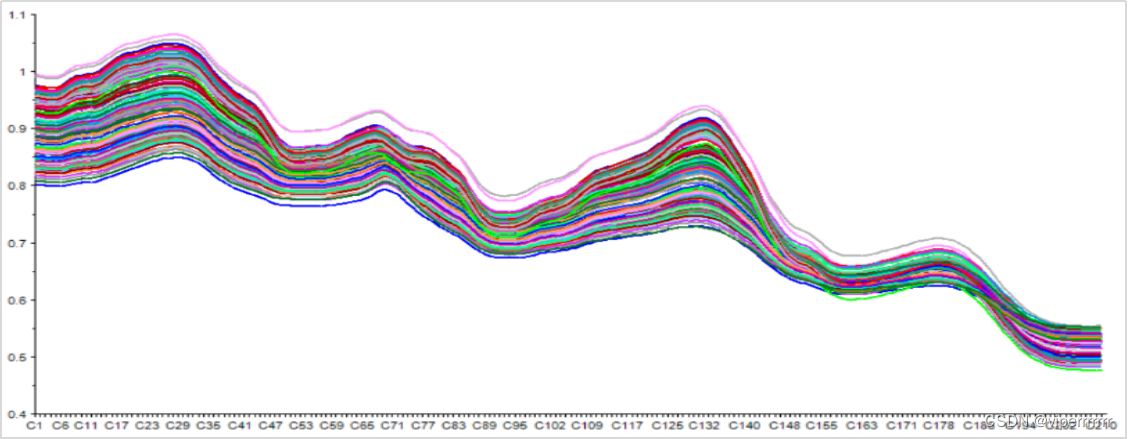
图2 5倍滑动滤波处理后数据图
5.1.2主成分分析模型
根据问题一的分析,我们建立了主成分分析模型进行了对不同包衣时间段包衣片剂的近红外光谱的特征峰选取。首先,将波长定义为X轴,在不同包衣时间下的片剂包衣、素片为Y 轴,在此基础上进行主成分分析,在进行特征根选取时,发现有两种情况可以选择,第一种情况是选取特征根大于1的成分,可以选取出2个主成分,第二种情况是按照公式(1)算取方差贡献率以选取特征根,可以选取出3个主成分。再算取累计方差贡献率以验证特征峰选取的合理性[2]。
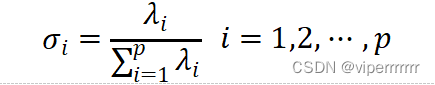 | (1) |
通过minitab(见附录)从中提取的2个主成分的特征值,对第一种情况进行分析,见图3,可知其得分向量(具体见附录)和特征根为:

,方差累计贡献率。说明选取的这两个主成分可以解释99.785%的原数据,具有较强的代表性。再对第二种情况进行分析,可以得到特征根和方差贡献率,方差累计贡献率
。
说明选取的这三个主成分可以解释99.897%的原数据,具有更强的代表性。但是对比第一种情况,代表性并提升幅度过小,综合考虑后,最终在问题一中选取第一种情况,即两个主成分为最终解。
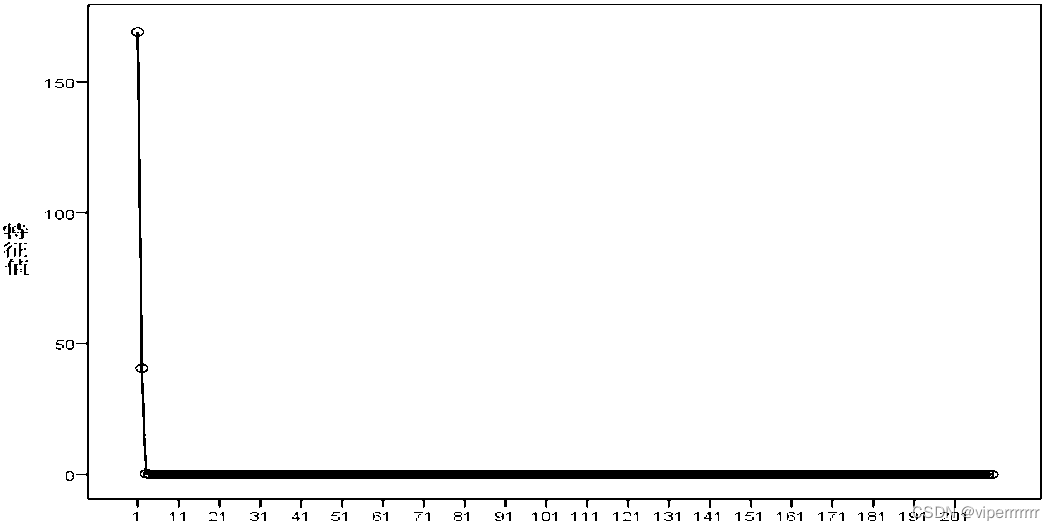
图3 主成分分析碎石图
这篇关于数学建模-最优包衣厚度终点判别法(主成分分析)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







