本文主要是介绍【MATLAB源码-第176期】基于matlab的16QAM调制解调系统频偏估计及补偿算法仿真,对比补偿前后的星座图误码率。,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
操作环境:
MATLAB 2022a
1、算法描述
在通信系统中,频率偏移是一种常见的问题,它会导致接收到的信号频率与发送信号的频率不完全匹配,进而影响通信质量。在调制技术中,QPSK(Quadrature Phase Shift Keying,四相位移键控)和QAM(Quadrature Amplitude Modulation,正交幅度调制)是两种常用的方法,它们可以高效地在给定的频带宽度内传输数据。然而,这两种调制方式都可能受到频偏(频率偏移)的影响。因此,准确估计和补偿这种频偏是提高通信系统性能的关键。
频偏的成因及影响
频偏主要由硬件的非理想特性引起,如本振(Local Oscillator,LO)的不稳定性、信号路径中的温度变化等。此外,移动通信中的多普勒效应也是引起频偏的一个重要因素。频偏不仅会导致接收信号的相位旋转,还会引起相位噪声,降低信号的信噪比(SNR),最终影响数据的解调效果和系统的整体性能。
频偏估计的重要性
在数字通信中,尤其是在使用QPSK和QAM这类高效调制技术的场合,准确估计频偏成为确保通信质量的关键步骤。通过准确估计出来的频偏值,可以相应地调整接收信号,补偿这一偏移,恢复出准确的信号,保证信息能正确无误地被接收方解调。
频偏估计算法的一般流程
频偏估计算法通常包含以下几个步骤:
-
信号接收与预处理:首先,接收到的信号会经过一系列预处理步骤,包括放大、滤波等,以提高信号质量。
-
信号转换与提取:将接收到的模拟信号转换为数字信号,然后从中提取I(In-phase)和Q(Quadrature-phase)两个分量,这两个分量包含了信号的幅度和相位信息。
-
频偏的初始估计:通过对信号的特定处理,如利用信号的周期性特征,初步估计出频偏的大小。这一步通常涉及复杂的数学运算,包括傅里叶变换(FFT)、角度计算等。
-
频偏的精确估计:在获得初步估计值后,通过进一步的算法优化,如最小二乘法、卡尔曼滤波等,对频偏的估计值进行精确调整,以获得更加准确的频偏值。
-
频偏补偿:最后,根据估计出的频偏值对接收信号进行相应的频率调整,补偿频偏,从而恢复出准确的原始信号。
算法实现的挑战与对策
实现频偏估计算法时,需要考虑多种因素:
-
算法的复杂度:算法需要在满足准确度要求的同时,尽可能降低计算复杂度,以适应实时或近实时的通信系统。
-
环境变化的适应性:算法需要能够适应信号传输过程中可能遇到的各种变化,如多路径传播、信号衰减等。
-
硬件限制:算法实现还需要考虑硬件的限制,比如处理器的计算能力、内存大小等。
为了解决这些挑战,频偏估计算法的设计通常会采用多种策略,包括算法优化、自适应算法设计、以及利用先进的数字信号处理技术等。
结语
频偏估计是数字通信中一个复杂但至关重要的问题,尤其是在使用高效调制技术如QPSK和QAM的现代通信系统中。一个准确有效的频偏估计算法可以显著提高通信质量和系统性能。随着通信技术的发展,频偏估计和补偿技术也在不断进步,为通信系统的稳定运行和发展提供了重要支撑。
2、仿真结果演示
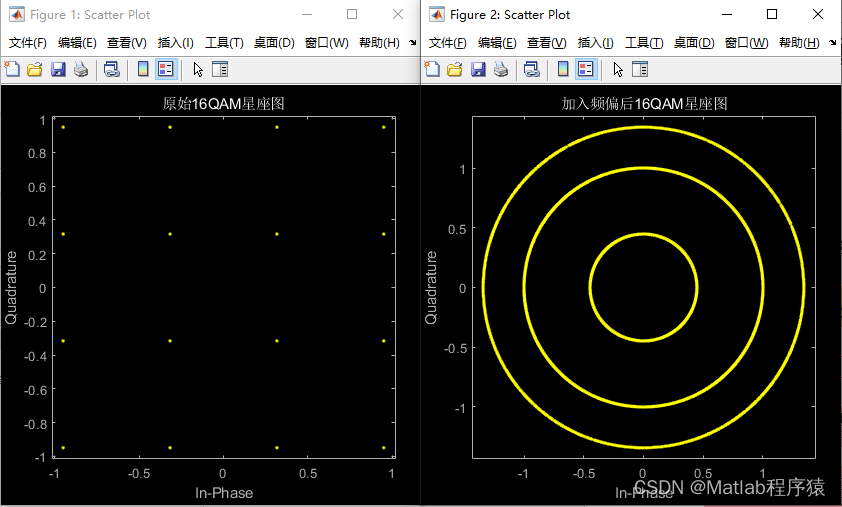

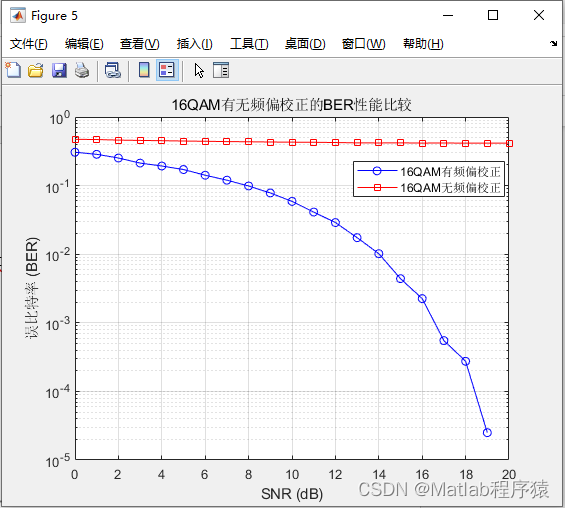
3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片
这篇关于【MATLAB源码-第176期】基于matlab的16QAM调制解调系统频偏估计及补偿算法仿真,对比补偿前后的星座图误码率。的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







