本文主要是介绍微生物群落关键种识别:一种不依赖于网络的自上而下的方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
微生物群落在促进养分循环、协助植物生长、维持人体健康等方面发挥着重要的作用。群落关键种对维持微生物群落稳定性具有重要影响,识别关键种一直是微生物生态学中的热点话题。识别关键种主要有两种框架:数据驱动的方法(data driven method)和去除实验(perturbation experiment)。其中数据驱动的方法主要有三种:
- 基于共现网络的方法
- top-down方法
- 基于深度学习的方法
注意:数据驱动的方法确定的关键种只是可能的关键种,还需要通过去除实验进一步地验证。
- 基于共现网络的方法主要包括:构建共现网络→划分模块→计算模块间连通度和模块内连通度→确定关键种,该方法已在之前的博客中有所介绍:计算网络节点模块内连通度(within modular degree)和模块间连通度(between modular degree)。
- 基于深度学习的方法:这里先做个预告,代码和数据都整理好了,预计下周上线,具体可参考论文
Identifying keystone species in microbial communities using deep learning。- 本文主要介绍
top-down方法,该方法源于论文:Top-down identification of keystone taxa in the microbiome。该方法通过计算Empirical Presence-abundance Interrelation (EPI)来衡量物种的重要性。
EPI指标计算的流程是:
- 根据物种i的有-无划分为两组:
有和无; - 将该物种去除,并将剩余物种的相对丰度标准化,使其和为1;
- 然后计算
有组和无组的距离,即该物种的重要性,EPI; - 物种EPI高于
平均值+两个标准差的物种可以确定为关键种。
这里的某物种 i i i 的EPI有三种衡量方法:
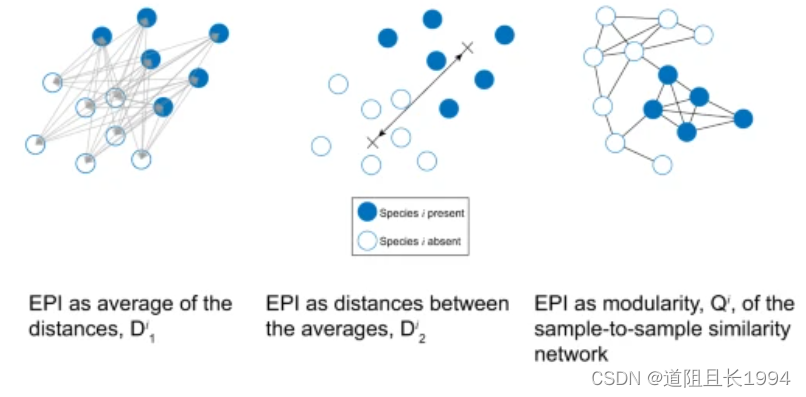
D 1 i {D}_{1}^{i} D1i 的计算:
- 根据物种 i i i 的有-无划分为两组:
有和无; - 将该物种去除,并将剩余物种的相对丰度标准化,使其和为1;
- 计算
有组和无组样品的两两间的Bray-Crutis距离。假设有5个样品A、B、C、D、E,其中有组:A、B、C,无组: D、E。有组和无组样品的两两间的距离矩阵为:
| ID | A | B | C |
|---|---|---|---|
| D | xxx | xxx | xxx |
| E | xxx | xxx | xxx |
- 然后取该矩阵的平均值,即为 D 1 i {D}_{1}^{i} D1i
计算 D 1 i {D}_{1}^{i} D1i R代码如下:
EPI_D1 <- function(S) {library(vegan)# InitializationN <- nrow(S)M <- ncol(S)S_01 <- ifelse(S>0,1,0)D1 <- rep(NA, N)for (i in 1:N) {# If the species is always present/absent, D1 is undefinedif (sum(S_01[i, ], na.rm = TRUE) != 0 & sum(S_01[i, ], na.rm = TRUE) != M) {print(i)ind_pres <- S_01[i, ] != 0S2 <- S[-i, , drop = FALSE]S2 <- S2 / colSums(S2)bc <- as.matrix(vegdist(t(S2)))bc2 <- bc[ind_pres,!ind_pres]D1[i] <- sum(bc2) / (sum(ind_pres) * sum(!ind_pres))}}return(D1)
}
D 2 i {D}_{2}^{i} D2i 的计算:
- 根据物种 i i i 的有-无划分为两组:
有和无; - 将该物种去除,并将剩余物种的相对丰度标准化,使其和为1;
- 分别计算
有组和无组样品的平均物种组成,获得 P ‾ \overline P P (P: Presence)和 A ‾ \overline A A (A: Absence),然后计算两者的平均值。假设有5个样品A、B、C、D、E,其中有组:A、B、C,无组: D、E。有组和无组样品平均值如下:
| ID | A | B | C | P ‾ \overline P P |
|---|---|---|---|---|
| taxa1 | x1 | x2 | x3 | average(x1,x2,x3) |
| taxa2 | y1 | y2 | y3 | average(y1,y2,y3) |
| taxa3 | z1 | z2 | z3 | average(z1,z2,z3) |
| ID | C | D | A ‾ \overline A A |
|---|---|---|---|
| taxa1 | x1 | x2 | average(x1,x2) |
| taxa2 | y1 | y2 | average(y1,y2) |
| taxa3 | z1 | z2 | average(z1,z2) |
- 然后计算 P ‾ \overline P P和 A ‾ \overline A A的Bray-Crutis距离,即为 D 2 i {D}_{2}^{i} D2i
计算 D 2 i {D}_{2}^{i} D2i R代码如下:
EPI_D2 <- function(S) {N <- nrow(S)M <- ncol(S)S_01 <- ifelse(S>0,1,0)D2 <- rep(NA, N)for (i in 1:N) {# If the species is always present/absent, D2 is undefinedif (sum(S_01[i, ], na.rm = TRUE) != 0 & sum(S_01[i, ], na.rm = TRUE) != M) {print(i)# Dividing into the two groupsind_pres <- S_01[i, ] != 0S_pres <- as.matrix(S[, ind_pres])S_abs <- as.matrix(S[, !ind_pres])# Removing the i speciesS_pres <- S_pres[-i, , drop = FALSE]S_abs <- S_abs[-i, , drop = FALSE]# NormalizingS_pres <- S_pres / colSums(S_pres)S_abs <- S_abs / colSums(S_abs)# Calculating D2D2[i] <- vegdist(rbind(rowMeans(S_pres), rowMeans(S_abs)))[1]}}return(D2)
}
Q i {Q}^{i} Qi 的计算:
- 根据物种 i i i 的有-无划分为两组:
有和无; - 将该物种去除,并将剩余物种的相对丰度标准化,使其和为1;
- 计算样品间的Bray-Crutis距离;
- 设定一定的阈值,构建
样品-样品的网络,这里网络中的节点代表样品; - 对网络中的节点(代表样品)赋予模块,例如:
模块1代表无,模块2代表有 - 计算该网络的
模块度(modularity),即为 Q i {Q}^{i} Qi
计算 Q i {Q}^{i} Qi 的R代码如下:
EPI_Q <- function(S, threshold_net) {N <- nrow(S)M <- ncol(S)S_01 <- ifelse(S > 0,1,0)Q <- rep(NA, N)modularity <- function(B, s) {library(igraph)B_graph <- graph.adjacency(B, mode = "undirected")d <- degree(B_graph) # Degree of each sampleq <- sum(B) / 2Qmod <- (t(s) %*% (B - (d %*% t(d)) / (2 * q)) %*% s) / (4 * q)return(Qmod)}for (i in 1:N) {# If the species is always present/absent, Q is undefinedif (sum(S_01[i, ], na.rm = TRUE) != 0 & sum(S_01[i, ], na.rm = TRUE) != M) {print(i)# Removing the i speciesS_i <- S[-i,]# NormalizingS_i <- S_i / colSums(S_i)# Building the networkdistances_i <- as.matrix(vegdist(t(S_i)))dist_threshold <- quantile(distances_i, threshold_net)B_i <- as.matrix(distances_i <= dist_threshold)diag(B_i) <- 0s_i <- as.numeric(S_01[i, ])s_i[s_i == 0] <- -1# CalculatingQ[i] <- modularity(B_i, s_i)}}return(Q)
}
更多测试数据及R代码可参考如下连接:https://mbd.pub/o/bread/ZZ2bm5hx
这篇关于微生物群落关键种识别:一种不依赖于网络的自上而下的方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




