本文主要是介绍路径规划——曲线拟合详解(一):多项式轨迹与QP优化(minimum-snap算法核心部分),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
历经一个多星期时间,我们在路径规划——搜索算法部分讲解了7种常见的路径搜索算法,每一种算法的链接放在下面了,有需要的朋友点击跳转即可:
路径规划——搜索算法详解(一):Dijkstra算法详解与代码_dijkstrac代码实现-CSDN博客
路径规划——搜索算法详解(二):Floyd算法详解与MATLAB代码-CSDN博客
路径规划——搜索算法详解(三):RRT算法详解与MATLAB代码-CSDN博客
路径规划——搜索算法详解(四):A*算法详解与C++代码-CSDN博客
路径规划——搜索算法详解(五):Dynamic A Star(D*)算法详解与Matlab代码-CSDN博客
路径规划——搜索算法详解(六):LPA*算法详解与Matlab代码-CSDN博客
路径规划——搜索算法详解(七):D*lite算法详解与Matlab代码-CSDN博客
以上所有算法的仿真都在笔者github上了:GitHub - Adamaser/Path-Planning
路径规划问题可以粗糙地划分为两个步骤:路径搜索与轨迹优化, 路径搜索生成可行的折线路径,但是不符合无人机、无人车的动力学,不能够直接输出给无人机、无人车直接执行。所以此时就需要进行轨迹优化,结合机器人的运动学模型,采用合适的曲线进行轨迹优化,生成光滑可行且符合机器人运动学的路径,由于笔者是做无人机方向的,所以在曲线拟合这一章中将以生成符合无人机运动学的轨迹为例讲解轨迹优化的知识。
曲线拟合部分将介绍两种无人机中常用的曲线,即多项式拟合与B样条拟合,由于其极具工程意义,所以曲线篇将会提供C++代码并且在ROS环境下进行仿真,大家可以看作是minimum-snap算法的复现,希望对大家有所帮助!
一、多项式轨迹介绍:
1.无人机的微分平坦特性

无人机12个状态量,分别为x、y、z三个维度上的位置、速度、角度、角速度,其符号表示如下:
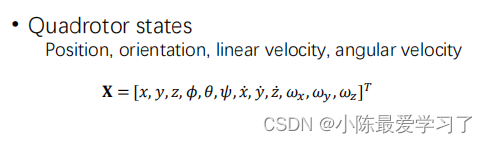
微分平坦特性指的是可以通过对输入的高阶导数进行显示表示,以简化轨迹设计与跟踪控制的表达,可以通过选择合理的控制量对系统的控制空间进行有效降维。
简言说之,就是原有的状态空间有12个量,他们并不是相互之间互不关联的,我们从里面得到几个状态量,通过这些状态量及其高阶导数可以直接求出其他状态量,经过证明,无人机具有微分平坦特性,其状态量可以简化为以下四个量表示:
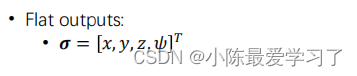
具体的证明过程大家直接搜索就可以看到很多帖子,这里就不多介绍了,所以我们可以直接通过控制x、y、z、yaw角就可以控制无人机的姿态。
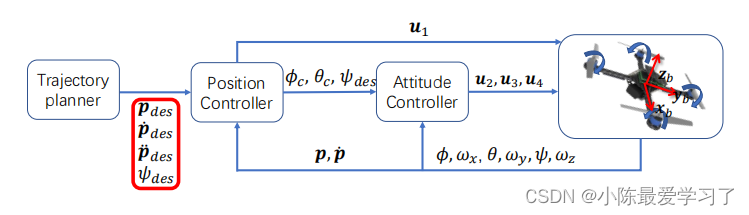
2.多项式轨迹表示与约束构建:
多项式轨迹是一种常见的曲线,根据多项式的最高次数可以分为一次、二次、...、N次多项式,我们需要怎么选择次数呢,我们以五次多项式为例:
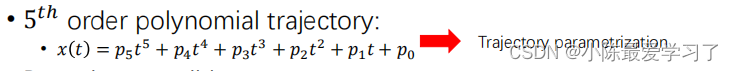
如上所示,五次多项式一共拥有p0-p5六个求解的自由度,我们可以添加6个约束条件以求得p0-p5,如下所示,我们可以先通过路径搜索算法得到如下的折线(黑色)轨迹:
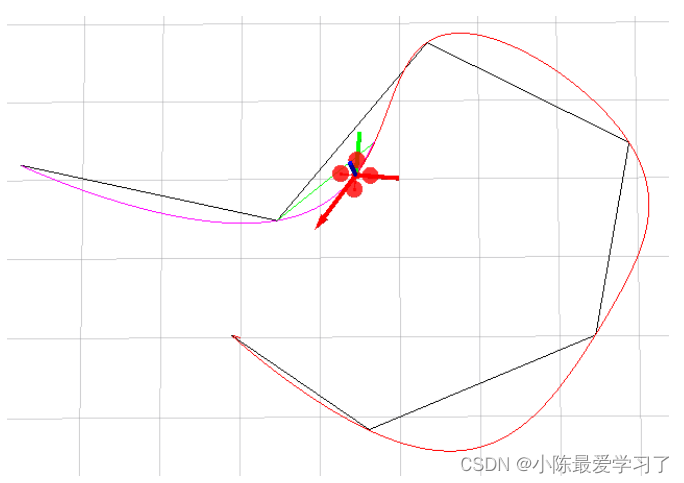
我们对每段轨迹进行多项式的拟合,然后连接每一段轨迹的头与尾就可以得到一条连续的多项式轨迹,对于每一条折线轨迹,假设曲线表示为x(t),可以根据需要对起点位置x(0)、终点位置x(T)、起点速度x‘(0)、终点速度x’(T)、起点加速度x‘’(0)、终点加速度x‘’(T)进行约束:
假设此时的约束条件如下:

我们将起点t=0、终点t=T带入以下多项式中:
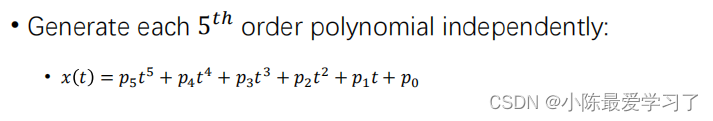
此外x(t)求导一次后再将起点t=0、终点t=T带入可以得到该时刻的速度、再次求导带入可以得到起点t=0、终点t=T处的加速度,此时我们将其写成矩阵形式可以得到以下的矩阵方程:

求解后我们便可得到满足上述约束条件所对应的p0-p5,此时便可以准确地表达出t=0到t=T时刻的多项式曲线,该曲线满足起点与终点的位置、速度、加速度条件。
以上求解x维度上的多项式曲线,同理我们可以求出y、z维度上的曲线,它们轨迹在各个坐标轴上是独立的,因此我们可以对其分别进行轨迹拟合。也就是说我们可以分别对它们在x , y , z进行路径生成,然后直接将三个轴合成就可以得到一个完整的空间轨迹。
3.minimum-snap算法(PPT来自深蓝学院课程笔记):
基于此思想,我们分段表示每一段折线轨迹:
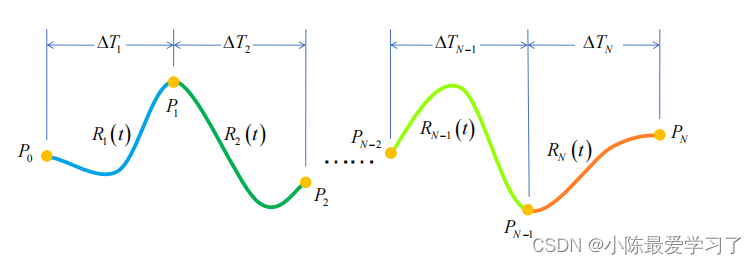
采用分段的方式表示其轨迹:
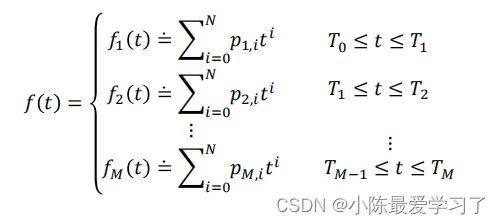
f(t)为位置、f'(t)为速度、f''(t)加速度、f'''(t)为加加速度jerk、f''''(t)为加加加速度snap,jerk可以影响无人机在该维度上的角速度,而jerk可以影响该维度上的角加速度,如下图所示:
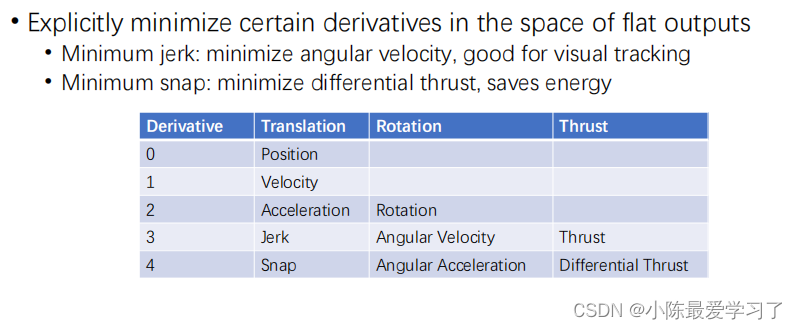
以minimum-snap为例,由于我们要对其求4次导数,需要保证jerk是连续的(所以我们要对轨每一段轨迹的起点与终点的位置、速度、加速度、加加速度jerk进行约束,后面会说约束要怎么加),对于每一段轨迹累加其snap的最小值:

如上所示,累加每段轨迹的snap可以化为一个二次优化问题QP,通过求解该优化问题得到每一段轨迹的系数矩阵P,但是在求解之间我们需要将每一段轨迹的起点与终点的位置、速度、加速度约束加入到该优化问题中,可以通过以下方式构建约束:

通过上述方式,我们将起点与终点的导数约束统一为AP=D这一约束条件,所以我们需要求解的优化问题如下所示:

通过调用OOQP、Mosek等QP问题求解器即可得到每一段轨迹的多项式系数,即得到了该维度上的光滑曲线。
具体的大家参考该论文:
Mellinger D, Kumar V. Minimum snap trajectory generation and control for quadrotors[C]//Robotics and Automation (ICRA), 2011 IEEE International Conference on. IEEE, 2011: 2520-2525.
二、多项式轨迹仿真:
demo大家可以参考下笔者的Github吧(笔者版本为ubuntu18.04),手搓的,代码注释很详细,包括QP矩阵构建与求解都有:
Path-Planning/Astar_/src at main · Adamaser/Path-Planning (github.com)
将src放到工作空间中,直接catkin build编译,编译后运行:
roslaunch grid_path_searcher my_demo.launch 就可以直接看到效果(绿色折线为A*搜索结果)

这篇关于路径规划——曲线拟合详解(一):多项式轨迹与QP优化(minimum-snap算法核心部分)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






