算法沉淀 —— 动态规划篇（简单多状态dp问题下）

本文主要是介绍算法沉淀 —— 动态规划篇（简单多状态dp问题下），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

几乎所有的动态规划问题大致可分为以下5个步骤，后续所有问题分析都将基于此

• 1.、状态表示：通常状态表示分为以下两种，其中更是第一种为主。

  • 以i为结尾，dp[i] 表示什么，通常为代求问题（具体依题目而定）
  • 以i为开始，dp[i]表示什么，通常为代求问题（具体依题目而定）

• 2、状态转移方程
  *以上述的dp[i]意义为更具， 通过最近一步来分析和划分问题，由此来得到一个有关dp[i]的状态转移方程。

• 3、dp表创建，初始化

  • 动态规划问题中，如果直接使用状态转移方程通常会伴随着越界访问等风险，所以一般需要初始化。而初始化最重要的两个注意事项便是：保证后续结果正确，不受初始值影响；下标的映射关系。
  • 而初始化一般分为以下两种：
    • 直接初始化开头的几个值。
    • 一维空间大小+1，下标从1开始；二维增加一行/一列。

• 4、填dp表、填表顺序：根据状态转移方程来确定填表顺序。

• 5、确定返回值

一、买卖股票的最佳时机含冷冻期

【题目链接】：309. 买卖股票的最佳时机含冷冻期
【题目】：

 给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。​
 设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
 注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

【示例】：

输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

【分析】：
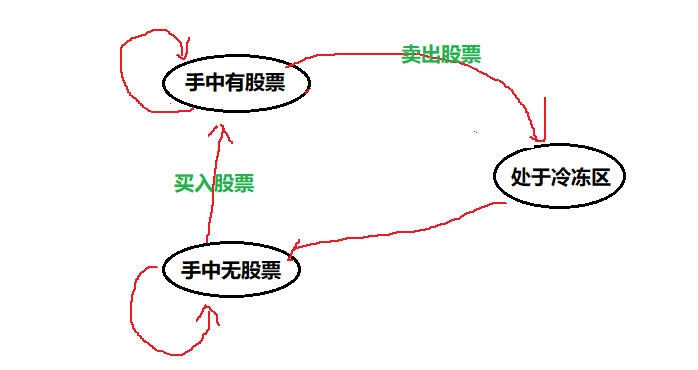
 我们可以定义dp[i]表示第i天结束后，买卖股票的最大利润。但我们发现第i天股票分为3种状态：手中有股票、无股票、处于冷冻区。所以我们可以定义一个（n x 3）的二维数组，其中dp[i][0]表示第i天结束后，手中有股票的最大利润；dp[i][1]表示第i天结束后，手中无股票的最大利润；dp[i][2]表示第i天结束后，股票处于冷冻区的最大利润。

状态转移方程推导：
 第i天结束后，手中有股票的情况可由：i-1天结束手中有股票第i天什么都不做、i-1天无股票在第i天买入股票两种情况得到。所以可得状态状态转移方程为 dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
 第i天结束后，手中无股票的情况可由：：第i-1天结束手中有股票在第i天卖掉股票、第i-1天股票处于冷冻区在第i天什么都不做两种情况得到。所以可得状态状态转移方程：dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
 第i天结束后，股票处于冷冻区只能由第i-1天手中有股票第i天将股票卖出所得。所以可得状态状态转移方程：dp[i][2] = dp[i - 1][0] + prices[i];

 初始化：显然当i为0时，状态转移方程不适应，需要特殊处理。这里我们可以将第0天的买卖股票状态直接初始化好(具体参考代码)。然后从第2天开始，填dp表！！
 最后返回第n天结束后，返回手中无股票和股票处于冷冻区的最大值即可！！
【代码编写】：

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(3));//初始化dp[0][0] = -prices[0];//第1天买人股票//填表for(int i = 1; i < n; i++){dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);dp[i][2] = dp[i - 1][0] + prices[i];}return max(dp[n - 1][1], dp[n - 1][2]);}
};

二、买卖股票的最佳时机含手续费

【题目链接】：714. 买卖股票的最佳时机含手续费
【题目】：

 给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。
 你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。
 返回获得利润的最大值。
 注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

【示例】：

输入：prices = [1, 3, 2, 8, 4, 9], fee = 2
输出：8
解释：能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8

【分析】：
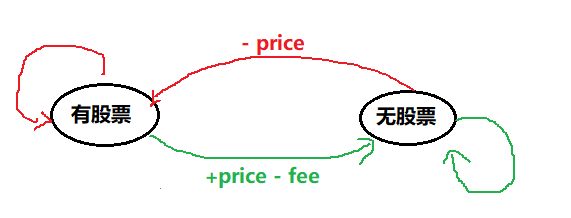
 我们可以定义dp[i]表示第i天结束后，所得最大利润。但第i天可以细分为手中有无股票。所以我们可以创建一个（n x 2）的数组，其中dp[i][0]表示第i天结束后，手中还有股票，此时所得的最大利润；dp[i][1]表示第i天结束后，手中无股票，此时所得的最大利润。

状态转移方程推导：
 dp[i][0]可以由：第i-1天后手中有股票并且第i天啥都不干、第i-1天后手中无股票并且第i天买入股票，所以状态转移方程为：dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);。
 ;dp[i][1]可以由：第i-1天后手中无股票并且第i天啥都不干、第i-1天后手中有股票并且第i天卖出股票（此时一次交易完成，需要将费用fee减掉），所以状态转移方程为：dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);

 初始化：显然当i为0时，状态转移方程错误。所以我们可以先初始化dp[0][0]、dp[0][1]（即第1天结束后，股票和利润的情况，具体参考代码）。
 然后从左往右填dp表，最后返回第n天结束后手中无股票的最大值即可！！

【代码编写】：

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(2));//初始化dp[0][0] = -prices[0];for(int i = 1; i < n; i++){dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);}return dp[n - 1][1];}
};

三、买卖股票的最佳时机 IV

【题目链接】：买卖股票的最佳时机 IV
【题目】：

 给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。
&emsp设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。
&emsp注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

【示例】：

输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

【分析】：
 我们可以定义dp[i[表示第i天结束后，在最多可以完成 k 笔交易的情况下，买卖股票的获得的最大利润。但我们发现第i天的股票状态还可以细分:手中有无股票，已经交易几次（从0~k次）。所以我们可以创建两个(n x (k + 1))的二维数组f和g：其中f[i][j]表示第i天结束后，完成j次交易，并且手中有股票时所得利润最大值；g[i][j]表示第i天结束后，完成j次交易，并且手中无股票时所得利润最大值。

状态转移方程推导：（我们定义只有当股票卖出时，交易才算完成，次数+1）
 f[i][j]可由：(第i-1天结束后，完成j次交易，并且手中有股票(即f[i-1][j])，在第i天不交易)、（第i-1天结束后，完成j次交易，并且手中无股票(即g[i-1][j])，在第i天买入股票）两种方式得到。所以状态转移方程：f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);

 g[i][j]可由：（第i-1天结束后，完成j次交易，并且手中无股票(即g[i-1][j])，在第i天不交易）、（第i-1天结束后，完成j-1次交易(第i-1天完成交易，此时交易次数加1得到j次)，并且手中有股票(即g[i-1][j])，在第i天卖出股票）两种方式得到。所以状态转移方程：g[i][j] = max(g[i-1][j], f[i-1][j-1] + price[i]);
细节处理：

 显然当i为0时，f的状态转移方程不适用，需初始化第1行；但对于g来说，i=0和j=0时，状态转移方程都不适用，需要初始化第一行和第一列。又因为当j=0时，对于g来说此时手中无股票且完成0次交易，没有意义。所以我们对g的状态转移方程仅需转换:

if(j >= 1)g[i][j] = max(g[i-1][j], f[i-1][j-1] + price[i]);

 此时，我们只需要初始化f和g的第一行即可。由于本体种交易次数有限制，我们应当珍惜交易此时。所以我们在第一次时，不仅需交易。此时我们仅需初始化f[0][0]、g[0][0]即可。同时为了防止第一行，d[0][0]和f[0][0]后的数据对后续填表造成影响，我们需将d表和f表中相应的值初始化INT_MIN。
但此时使用状态转移方程可能发生越界，所以我们将INTMIN改为其一半0x3f3f3f3f。
【代码编写】：

class Solution {
public:const int KNF = 0x3f3f3f3f;//INT_MAX一半int maxProfit(int k, vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n, vector<int>(k + 1, -KNF));auto g = f;//初始化f[0][0] = -prices[0], g[0][0] = 0;for(int i = 1; i < n; i++)for(int j = 0; j <= k; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if(j >= 1)g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);}int ret = -KNF;for(int j = 0; j <= k; j++)ret = max(ret, g[n - 1][j]);return ret;}
};

这篇关于算法沉淀 —— 动态规划篇（简单多状态dp问题下）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---