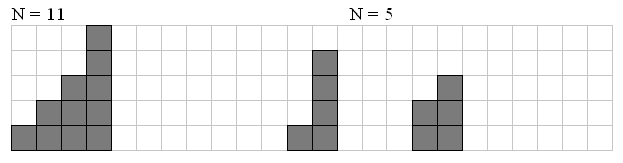dp专题
hdu4826(三维DP)
这是一个百度之星的资格赛第四题 题目链接:http://acm.hdu.edu.cn/contests/contest_showproblem.php?pid=1004&cid=500 题意:从左上角的点到右上角的点,每个点只能走一遍,走的方向有三个:向上,向下,向右,求最大值。 咋一看像搜索题,先暴搜,TLE,然后剪枝,还是TLE.然后我就改方法,用DP来做,这题和普通dp相比,多个个向上
hdu1011(背包树形DP)
没有完全理解这题, m个人,攻打一个map,map的入口是1,在攻打某个结点之前要先攻打其他一个结点 dp[i][j]表示m个人攻打以第i个结点为根节点的子树得到的最优解 状态转移dp[i][ j ] = max(dp[i][j], dp[i][k]+dp[t][j-k]),其中t是i结点的子节点 代码如下: #include<iostream>#include<algorithm
hdu4865(概率DP)
题意:已知前一天和今天的天气概率,某天的天气概率和叶子的潮湿程度的概率,n天叶子的湿度,求n天最有可能的天气情况。 思路:概率DP,dp[i][j]表示第i天天气为j的概率,状态转移如下:dp[i][j] = max(dp[i][j, dp[i-1][k]*table2[k][j]*table1[j][col] ) 代码如下: #include <stdio.h>#include
usaco 1.1 Broken Necklace(DP)
直接上代码 接触的第一道dp ps.大概的思路就是 先从左往右用一个数组在每个点记下蓝或黑的个数 再从右到左算一遍 最后取出最大的即可 核心语句在于: 如果 str[i] = 'r' , rl[i]=rl[i-1]+1, bl[i]=0 如果 str[i] = 'b' , bl[i]=bl[i-1]+1, rl[i]=0 如果 str[i] = 'w', bl[i]=b
uva 10154 DP 叠乌龟
题意: 给你几只乌龟,每只乌龟有自身的重量和力量。 每只乌龟的力量可以承受自身体重和在其上的几只乌龟的体重和内。 问最多能叠放几只乌龟。 解析: 先将乌龟按力量从小到大排列。 然后dp的时候从前往后叠,状态转移方程: dp[i][j] = dp[i - 1][j];if (dp[i - 1][j - 1] != inf && dp[i - 1][j - 1] <= t[i]
uva 10118 dP
题意: 给4列篮子,每次从某一列开始无放回拿蜡烛放入篮子里,并且篮子最多只能放5支蜡烛,数字代表蜡烛的颜色。 当拿出当前颜色的蜡烛在篮子里存在时,猪脚可以把蜡烛带回家。 问最多拿多少只蜡烛。 代码: #include <iostream>#include <cstdio>#include <cstdlib>#include <algorithm>#include <cs
uva 10069 DP + 大数加法
代码: #include <iostream>#include <cstdio>#include <cstdlib>#include <algorithm>#include <cstring>#include <cmath>#include <stack>#include <vector>#include <queue>#include <map>#include <cl
uva 10029 HASH + DP
题意: 给一个字典,里面有好多单词。单词可以由增加、删除、变换,变成另一个单词,问能变换的最长单词长度。 解析: HASH+dp 代码: #include <iostream>#include <cstdio>#include <cstdlib>#include <algorithm>#include <cstring>#include <cmath>#inc
XTU 1233 n个硬币连续m个正面个数(dp)
题面: Coins Problem Description: Duoxida buys a bottle of MaiDong from a vending machine and the machine give her n coins back. She places them in a line randomly showing head face or tail face o
dp算法练习题【8】
不同二叉搜索树 96. 不同的二叉搜索树 给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: 输入:n = 3输出:5 示例 2: 输入:n = 1输出:1 class Solution {public int numTrees(int n) {int[] dp = new int
hdu3006状态dp
给你n个集合。集合中均为数字且数字的范围在[1,m]内。m<=14。现在问用这些集合能组成多少个集合自己本身也算。 import java.io.BufferedInputStream;import java.io.BufferedReader;import java.io.IOException;import java.io.InputStream;import java.io.Inp
ural 1297. Palindrome dp
1297. Palindrome Time limit: 1.0 second Memory limit: 64 MB The “U.S. Robots” HQ has just received a rather alarming anonymous letter. It states that the agent from the competing «Robots Unli
ural 1017. Staircases DP
1017. Staircases Time limit: 1.0 second Memory limit: 64 MB One curious child has a set of N little bricks (5 ≤ N ≤ 500). From these bricks he builds different staircases. Staircase consist
ural1009 数位dp
1009. K-based Numbers Time limit: 0.5 second Memory limit: 64 MB Let’s consider K-based numbers, containing exactly N digits. We define a number to be valid if its K-based notation doesn’
概率DP (由一道绿题引起的若干问题。目前为一些老题,蒟蒻的尝试学习1.0)
概率DP: 利用动态规划去解决 概率 期望 的题目。 概率DP 求概率(采用顺推) 从 初始状态推向结果,同一般的DP类似,只是经历了概率论知识的包装。 老题: 添加链接描述 题意: 袋子里有w只白鼠,b只黑鼠,A和B轮流从袋子里抓,谁先抓到白色谁就赢。A每次随机抓一只,B每次随机 抓完一只后 会有另外一只随机老鼠跑出来。如果两个人都没有抓到白色,那么B赢。A先抓,问A赢得概率。 w b 均在
【POJ 3666】Making the Grade(简单DP)
首先可以明确一个方面,那就是如果将X改成Y,那么Y肯定是这N个数中的某一个(为什么仔细想想) 之后可以得到一个状态转移那就是dp[i][j]代表已经考虑了i位的情况下,结尾为j的最小更改数。 状态转移为dp[i][j] = min(dp[i-1][k] + abs(a[i] - b[j])) 这样的话可以写出一个初步的代码: #include<cstdio>#include<cst
CF#271 (Div. 2) D.(dp)
D. Flowers time limit per test 1.5 seconds memory limit per test 256 megabytes input standard input output standard output 题目链接: http://codeforces.com/contest/474/problem/D We s
dp(背包问题) 恰好、至少、至多初始化
状态表示的初始化(一般情况) f[i][j] i:前i件物品 体积至少为j 枚举体积时可以是负数(体积为负数时等价于体积为0) max f[i][j] = {-0x3f} f[i][0] = 0min f[i][j] = { 0x3f} f[i][0] = 0cnt f[0][0] = 1 体积至多为j 枚举体积时不能是负数 max f[i][j] = 0min f[i][j]
HDU 1428 漫步校园 (搜索 + dp)
OJ题目:click here ~~ 题意分析:题目中有句话“他考虑从A区域到B区域仅当存在一条从B到机房的路线比任何一条从A到机房的路线更近(否则可能永远都到不了机房了…)。”,关键是对这句话的理解。此刻在A区域,选择下面要走的B区域的条件是,存在一条B区域到机房的路线比A区域到机房的所有路线都近,也就是说,存在一条B区域到机房的路线比A区域到机房的最短路线更近(比最短的近
HDU 4035 Maze (树状dp + 概率)
OJ题目 : click here ~~~ 题目分析 :这篇文章已经说的很好很好了 , 直接借用 ,猛戳~~ int n;double k[10002] , e[10002];double A[10002] , B[10002] , C[10002];vector<int> List[10002];bool dfs(int u , int father){if(List[u].s
状态压缩dp(状压dp)
注:在涉及到位运算时,一定要注意位运算的优先级。该加的括号一定要加 状压dp是一类比较难理解的dp; 在讲状压dp之前,我们应该清楚所有的dp是解决多阶段决策最优化问题的一种思想方法; 请注意多阶段这三个字: 经过前面三种背包的学习,可以发现如何定义状态是解决动态规划最重要的一步; 状态的定义也就决定了相当于阶段的划分; 在背包问题中,我们通过物品的件数i和背包的容量j来定义状态或者说
dp子序列问题+时间复杂度分析
动态规划子序列问题, 把大的问题细化到一个点,先研究在这个小的点上如何解决问题,然后再通过递归/迭代的方式扩展到整个问题。 算法题到最后就是聪明的穷举,如何聪明的拆分问题。 对于两个字符串求子序列的问题,都是用两个指针 i 和 j 分别在两个字符串上移动,大概率是动态规划思路。 不要看 s1 和 s2 两个字符串,而是要具体到每一个字符,思考每个字符该做什么。 int dp(int i,
动态规划DP--背包问题
文章目录 0-1背包问题 -- 问题定义动态规划解法代码题目:分割等和子集题解 0-1背包问题 – 问题定义 在 0-1 背包问题中,给定一个背包的最大容量 W,以及 n 个物品,每个物品有两个属性: 重量:第 i 个物品的重量为 wt[i]价值:第 i 个物品的价值为 val[i] 目标是选择若干个物品装入背包,使得在不超过背包最大容量 W 的前提下,装入背包的物品的总价