算法系列--动态规划--特殊的状态表示--分析重复子问题

本文主要是介绍算法系列--动态规划--特殊的状态表示--分析重复子问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

💕"轻舟已过万重山!"💕
作者：Lvzi
文章主要内容：算法系列–算法系列–动态规划–特殊的状态表示–分析重复子问题

大家好,今天为大家带来的是算法系列--动态规划--特殊的状态表示--分析重复子问题

一.组合总数IV

链接:
https://leetcode.cn/problems/combination-sum-iv/
在这里插入图片描述
分析:

本题名字叫做组合问题,但实际上是一个排列问题,需要说明的是背包问题解决的是有限制条件下的"组合"问题,本题是一个排列问题,其实根本就无法使用背包问题的思路解决

那该如何解决呢?而且这道题还不太容易分析状态表示,其实这是动态规划问题中比较难的一种问题,状态表示的确立应该是:在分析问题的时候,发现重复的子问题,并抽象出状态表示

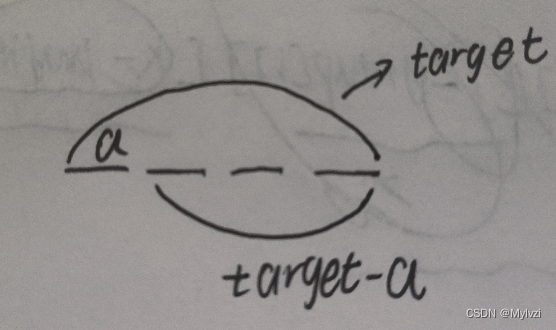
在这里插入图片描述
目的是求出总和等于target的所有排列方式,如果固定第一个数为a,那么就是求出总和等于target-a的所有排列方式,这里的重复子问题就是求出总和等于某个数的所有排列方式

状态表示:

dp[i]:总和等于i的所有排列方式

状态转移方程:
还是根据最后一个位置的状态划分问题
在这里插入图片描述
nums[j]表示的是数组中任意的一个数,只要符合条件(i >= nums[j]),都可以作为组成总和为i的排列方式的一种,那么只需在前面判断组成和为i-nums[j]的所有排列数即可,即dp[i - nums[j](注意本题是排列,排列!!!是区分顺序的!!!)

初始化:

dp[0] = 1:凑出总和为0的所有方式–>什么也不选–>空集也算一种情况

代码:

class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for(int i = 1; i <= target; i++)for(int j = 0; j < nums.length; j++)if(i >= nums[j])dp[i] += dp[i - nums[j]];return dp[target];}
}

根据状态表示可以推导出最后应该返回的结果为总和为target的所有排列方式,但是这些排列方式的组合中必须包含数组中的数字

二.不同的二叉搜索树

链接:
https://leetcode.cn/problems/unique-binary-search-trees/
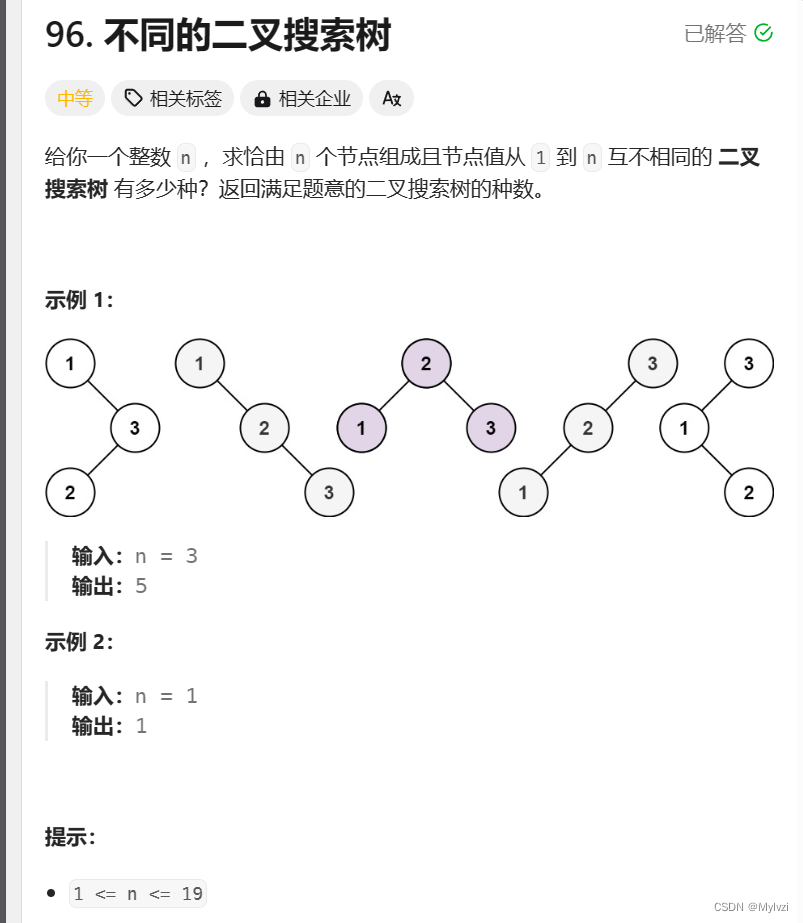
在这里插入图片描述
分析:

做之前一定要知道什么是二叉搜索树,二叉搜索树是指一课二叉树的所有子树都满足left < root < right

本题同样也可以采用在分析问题的时候,发现重复的子问题,并抽象出状态表示的分析方法
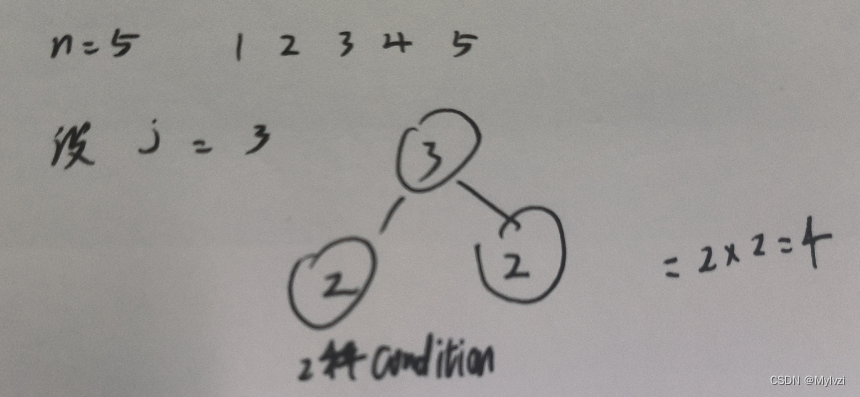
在这里插入图片描述
这里的重复子问题就是选择一个数作为根节点之后,统计其所有的情况,一直统计完所有的数

状态表示:

dp[i]:结点的个数为i时,一共有多少种二叉搜索树

状态转移方程:
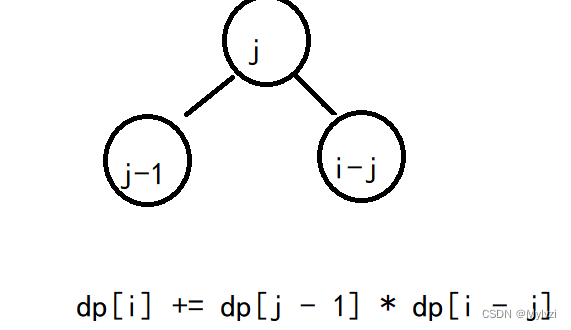
在这里插入图片描述

初始化:

dp[0] = 1:空树也算是二叉搜索树

代码:

class Solution {public int numTrees(int n) {int[] dp = new int[n + 1];dp[0] = 1;// 初始化for(int i = 1; i <= n; i++)// 枚举节点的总数for(int j = 1; j <= i; j++)// 选择每一个根节点dp[i] += dp[j - 1] * dp[i - j];// 填表return dp[n];}
}